
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение задачи о туннелировании
|
|
Наконец, следуя нашему принципу обучения посредством решения одних и тех же задач разными способами, повторим в Mathematica пример расчета прохождения частицы через одномерный прямоугольный потенциальный барьер [2, с. 101–102], разобранный в Теме 1. Программа имеет следующий вид (вместо E используем V).
u0=40; m=1/2; h=1;
(V> 0) ™ True
(V < u0) ™ True
Обратим внимание на формат оператора, присваивающего свойства переменным – аналог оператора assume в Maple. Далее описываем величину ε и уравнения:
epsilon=(2*m/h^2)*V;
eq1=f1''[x]+(2 m/h^2) V f1[x]Š 0
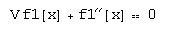
eq2=f2''[x]+(2 m/h^2) (EE-u0) f2[x]Š 0
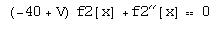
eq3=f3''[x]+(2 m/h^2) EE f3[x]Š 0
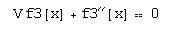
Очень важное наблюдение: в Mathematica есть три вида «знаков равенства»: обычный знак равенства =, двоеточие со знаком равенства: = и двойной знак равенства ==. Первый является оператором присваивания для символов (переменных), второй – оператором присваивания для функций, а третий является просто знаком равенства в соотношениях и уравнениях (т.е. когда он непосредственно ничего не присваивает). В Maple имеется лишь два таких знака, причем: = – это оператор присваивания и для символов, и для уравнений а = – это знак равенства в уравнениях.
r=DSolve[{eq1, eq2, eq3, f1[1]Š f2[1], f1'[1]Š f2'[1], f2[0]Š f3[0], f2'[0]Š f3'[0], f1[0]+I*f1[Pi/2/Sqrt[epsilon]]==2, f3[0]-I*f3[Pi/2/Sqrt[epsilon]]==0}, {f1[x], f2[x], f3[x]}, x]

Нельзя не обратить внимания, насколько компактнее, по сравнению с Maple, система Mathematica выдала решение! А ведь это то же самое решение, в чем мы сейчас убедимся. Это является проявлением уже упоминавшейся несколько большей оптимальности расчетов в Mathematica.
Выполняем операторы присваивания:
f1[x]=f1[x]/.r; f2[x]=f2[x]/.r; f3[x]=f3[x]/.r;
(структура операторов получилась несколько странная с точки зрения логики, но в каждой системе иногда надо подстраиваться под общее строение и синтаксис языка).
Вычисляем коэффициент прохождения (напомним, имея в виду (1.10), можно получить амплитуду прошедшей сквозь барьер волны S, просто подставив 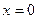 в
в 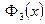 и далее вычисляя коэффициент прохождения как квадрат модуля S, умножая S на его комплексно сопряженное (оператор conjugate):
и далее вычисляя коэффициент прохождения как квадрат модуля S, умножая S на его комплексно сопряженное (оператор conjugate):
S=f3[x]/.x®0
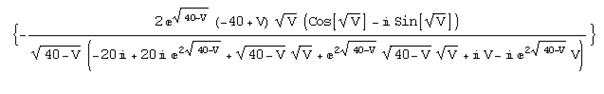
T=N[S Conjugate[S]];
Проверим, получили ли мы тот же результат, что и раньше, для чего вычислим коэффициент прохождения для энергии V=38:
T/.V®38
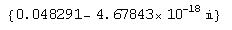
С помощью оператора Plot получаем хорошо знакомый график для коэффициента прохождения в зависимости от энергии
Plot[T/.V®Ex, {Ex, 0, 4*u0}]
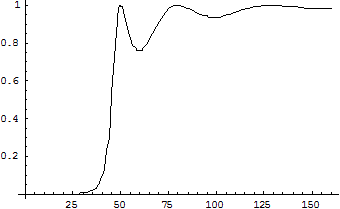
Рис. 3.4.Изменение коэффициента прохождения в зависимости от энергии для потенциального барьера, показанного на рисунке 1.4, полученное в Mathematica
Наконец, проверим еще раз соотношение (1.11), для чего вычислим коэффициент отражения (обозначим, как и выше, через 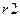 ). Функция ft представляет собой сумму коэффициентов прохождения и отражения. Так же как это было сделано в MATLAB, для ознакомления с циклами в Mathematica, произведем проверку не путем построения графика, а составим простейший цикл, выводя значения ft для пяти различных значений аргумента E:
). Функция ft представляет собой сумму коэффициентов прохождения и отражения. Так же как это было сделано в MATLAB, для ознакомления с циклами в Mathematica, произведем проверку не путем построения графика, а составим простейший цикл, выводя значения ft для пяти различных значений аргумента E:
r=(f1[x]-1)/.x®0; r2=N[r Conjugate[r]];
ft[q_]: =N[(T+r2)/.V®q];
nn=5; For[k=1, k< =nn, Print[ft[k*4*u0/nn]]; k++]
{1. +0. ä }
 .
.