
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Начальные навыки работы с MATLAB
|
|
Ознакомимся с работой MATLAB на практике. При запуске MATLAB появляется командное окно, в левой части которого возможно появление областей Command History – Перечень предыдущих команд, Current Directory – Браузер локального диска и др. (их можно вызывать или убирать с помощью опций в меню «Desktop»). Причем обычно в Command History по умолчанию загружается последний файл, с которым работали перед выключением системы.
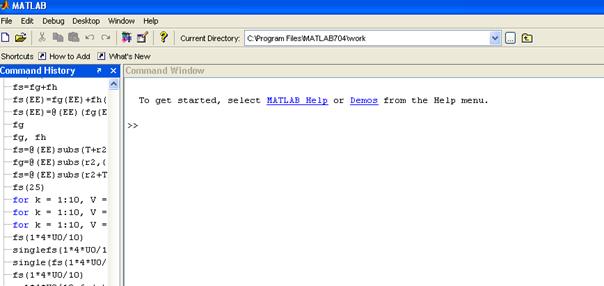
Рис. 2.1. Окно системы MATLAB после запуска
Например, на рисунке 2.1 изображено командное окно, которое появилось после запуска MATLAB в меню Пуск. Во время предыдущего использования были произведены простые действия, которые видны в левой части: переменным a и b были присвоены значения 2 и 3. Эти команды отобразились в Command History, но это не означает, что они выполнились, в чем легко убедиться, если попытаться использовать эти переменные:
> > a
??? Undefined function or variable 'a'.
> > a+b
??? Undefined function or variable 'a'.
> > b
??? Undefined function or variable 'b'.
Система не понимает, что мы от нее хотим. Загружен только список предыдущих команд, а сама Рабочая область (Workspace) – нет. Такая же ситуация, кстати, имеет место и в Maple, там при загрузке файла загружается текст программы, все команды которого надо выполнить, чтобы присвоить переменным и функциям их значения. Так же можно поступить в MATLAB, если вызывать предыдущие команды (по одной) стрелкой курсора вверх-вниз и выполнять их (этот прием создатели MATLAB явно заимствовали из теперь уже почти забытой DOS):
> > a=2; b=3;
> > a, b
a =
b =
3.
Обратим внимание: в MATLAB также используется точка с запятой для разделения операторов, но совершенно иначе, можно даже сказать, с противоположным значением, чем в Maple. Если в последнем точка с запятой означает команду выполнить оператор и распечатать результат его выполнения, то в MATLAB наоборот – это команда НЕ печатать! При этом команда «печатать» в MATLAB – это отсутствие какого-либо знака после оператора. Но тогда возникает проблема разделения операторов, записанных в одной строчке, что делается с помощью запятой, как продемонстрировано в вышеприведенном примере.
Такого рода различия между системами носят формально-синтаксический характер, и говорить о том, какой язык лучше и удобнее – сугубо дело вкуса и индивидуальных предпочтений. Но есть более глубокие различия между языками, которые носят, на наш взгляд, принципиальный характер. Вспомним, что до выполнения команды присваивания значений переменных a и b, система (MATLAB) вообще не допускала какого-либо использования этих символов, даже в ответ на простейшую команду «a» следовало «Undefined function or variable 'a'». А как поступит в такой ситуации (т.е. до загрузки или предварительного выполнения каких-либо команд) Maple? Вот так:
> a; a+b; t: =a-b;
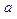
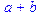
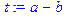 .
.
То есть в Maple любые символы по умолчанию предполагаются переменными (вообще говоря, комплексными), с которыми можно производить действия, определяя одни через другие. В MATLAB, как сразу же убеждается в этом любой, приступающий к его изучению, необходимо все описывать. Это, на наш взгляд, является неким «рудиментом», пришедшим из алгоритмических языков и делает язык MATLAB менее наглядным и удобным в применении, чем Maple. Можно сказать, что Maple намного более соответствует духу системы аналитических вычислений и компьютерной алгебры.
Продолжая первичное знакомство с MATLAB, отметим, что необязательно выполнять по одной все команды из файла (с расширением .mat), который вы хотите загрузить. Его можно загрузить с помощью команды «Open» из меню File (обычная процедура открытия файла в Windows). Интересно, что при выполнении этой процедуры вы не заметите никаких видимых изменений в командном окне. Изменения будут состоять в том, что в память загрузится рабочая область (Workspace), т.е. выполнятся все команды из загружаемого файла, в чем можно убедиться, выполняя какие-либо действия с переменными, которые там фигурируют.
В любой момент можно очистить Перечень команд, Командное окно и Рабочую область с помощью команд из меню Edit.
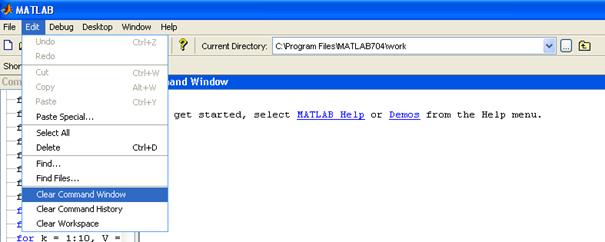
Рис. 2.2. Меню Edit в MATLAB
Обратим внимание, что выполнение команд «Clear Command Window» и «Clear Command History» не приводит к выгрузке рабочего файла из памяти и можно продолжать вычисления дальше. Лишь команда «Clear Workspace» очищает память и является аналогом команды «restart» в Maple.
Можно также загрузить рабочий файл, если запустить MATLAB, произведя двойной щелчок по значку этого файла. В этом случае в Command History сразу появится команда о загрузке файла (оператор load):
load('C: \DOCUME~1\admin\0016~1\matlab.mat').
Отсюда понятен синтаксис оператора load: в скобках и в одинарных кавычках «прописан путь» к вашему файлу. Такую команду можно напечатать и выполнить в рабочем окне и вручную, что также приведет к загрузке файла.
Читателю настоятельно рекомендуется проверить все вышеописанные процедуре на практике. А именно произвести следующие действия:
- запустите MATLAB из меню Пуск;
- очистите все с помощью команд «Clear Command Window», «Clear Command History» и «Clear Workspace» из меню Edit;
- произведите какие-либо действия в рабочем окне, например, вычисления, разобранные ниже в этой лекции и/или простейшие операции присваивания и арифметические действия;
- сохраните созданный вами файл с помощью команды «Save Workspace As» из меню File и закройте программу;
- снова запустите несколько раз MATLAB и загрузите ваш файл различными способами, описанными выше.
Для первичного знакомства с MATLAB, следуя принятому в данном пособии принципу производить одни и те же вычисления разными способами, повторим те простейшие операции, которыми иллюстрировалось изложение Maple в Теме 1. И здесь на первом же шаге мы сталкиваемся с тем принципиальным отличием от Maple, о котором говорилось выше:
> > a=2, b=3, f=sin(a*x)/x, g=cos(b*x)
a =
b =
??? Undefined function or variable 'x'.
Если оператор присваивания для a прошел без проблем, то попытка описать функции, даже в форме простых выражений, зависящих от переменной x, провалилась. Система не принимает переменную x, требуя ее описания. Ясно, что мы не можем продвинуться дальше, не обращаясь к Help.
Войдя в меню Help, выберем раздел MATLAB Help, в котором можно выбрать одну из вкладок представления справочного материала. Выберем вкладку Contents, которая представляет собой полное оглавление содержимого системы в виде «дерева». К нужному нам разделу об описании функций приходим по пути: MATLAB – Mathematics – Functions – Representing Functions in MATLAB. Попадаем на страницу, на которой изложено, как описывать функции.
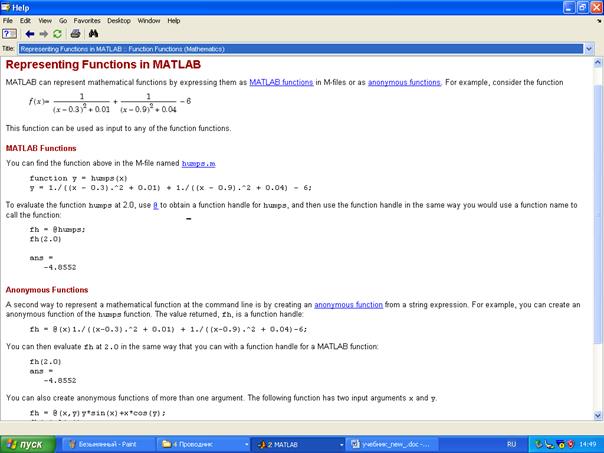
Рис. 2.3. Пользование справкой в MATLAB
Нам нужны в данном случае не функции, записанные в m -файлах (MATLAB Functions), а так называемые Anonymous Functions, под этим несколько странным названием фигурируют функции, задаваемые пользователем в ходе выполнения программы (в Maple это делается с помощью оператора x->). Таким образом, наши функции можно задать так:
> > f=@(x)sin(a*x)/x, g=@(x)cos(b*x)
f =
@(x)sin(a*x)/x
g =
@(x)cos(b*x).
Теперь функции f и g существуют в нашей рабочей области, в чем можно убедиться, вызвав их значения при каких-либо значениях x:
> > f(2), g(3)
ans =
-0.3784
ans =
-0.9111
или построив график (выдается в отдельном окне)
> > fplot(f, [-5 5]).
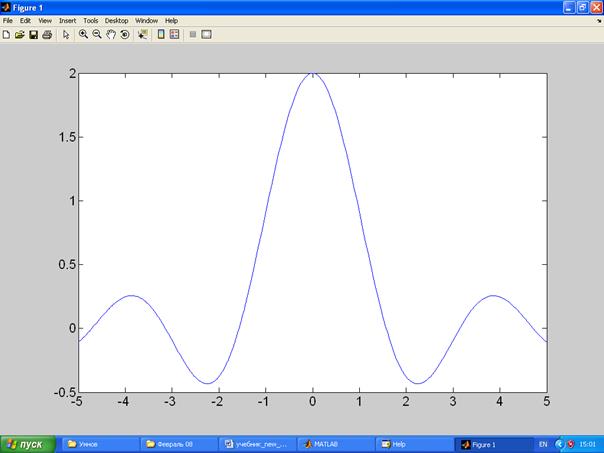
Рис. 2.4. Пример построения графика функции от одной переменной в MATLAB
Проведем также вычисление в MATLAB примера нахождения емкости трех последовательно включенных емкостей (конденсаторов) C1, C2 и C3 произвольной величины, разобранного в теме 1 в рамках Maple.
> > R=solve('1/c0=1/c1+1/c2+1/c3', 'c0')
R =
c1*c2*c3/(c2*c3+c1*c3+c1*c2)
> > c1=2; c2=1; c3=4;
> > subs(R)
ans =
0.5714
Обратим внимание, что здесь оператор subs, примененный к имени R, под которым фигурирует решение уравнения, действует так же, как оператор assign в Maple.
Примеры на дифференцирование и интегрирование, разобранные в теме 1, в MATLAB выглядят так (перед началом вычислений необходимо описать переменные, которые будут входить в выражения, как символические, с помощью оператора syms):
> > syms x
> > diff(sin(x)^2+cos(x)^3, 'x')
ans =
2*sin(x)*cos(x)-3*cos(x)^2*sin(x)
> > int(sin(x), x), int(sin(x), 0, pi)
ans =
-cos(x)
ans =
2.
Интегралы, выражающиеся через специальные функции и «неберущиеся»:
> > q1=int(exp(-x^2), -1, 1), q2=int(exp(-x^3), -1, 1)
q1 =
erf(1)*pi^(1/2)
Warning: Explicit integral could not be found.
> In sym.int at 58
q2 =
int(exp(-x^3), x = -1.. 1)
> > single(q1), single(q2)
ans =
1.4936
ans =
2.1494.
(сравните с численными значениями, полученными в Теме 1 с помощью Maple). Обратим внимание, что система предупреждает о том, что интеграл q2 не может быть вычислен в явном виде. Тем не менее, с помощью оператора single (который в данном случае действует так же, как evalf в Maple) он может быть найден численно (по поводу single и других операторов, имеющих отношение к типам данных, см. раздел Programming – Data Types в Help).