Начальное знакомство с системой Mathematica

Ознакомимся с работой системы на практике. Запустим программу из меню Пуск. Автоматически откроется новое рабочее поле в виде автономного окна (в Mathematica оно называется Notebook – блокнот). Можно открыть второе и большее количество таких окон. На рисунке 3.1 открыто два окна, и в них проведены простейшие вычисления.

Самое главное, что надо знать о Mathematica в отношении сравнения ее с другими системами компьютерной алгебры: ее язык внешне достаточно сильно отличается от языка Maple, но по внутреннему «устройству» и по приемам работы с интерфейсом весьма похож на него. Так что пользователь, владеющий, допустим, навыками работы с Maple, не испытает принципиальных неудобств при переходе на Mathematica, в отличие от MATLAB, который потребует от него значительной перестройки. А именно: в Mathematica, так же как в Maple, вы набираете оператор в командной строке и для его выполнения нажимаете Shift–Enter (отличие от Maple и MATLAB, где нажимается просто Enter – сравнение, конечно, не в пользу Mathematica, но при длительном пользовании это входит в привычку).

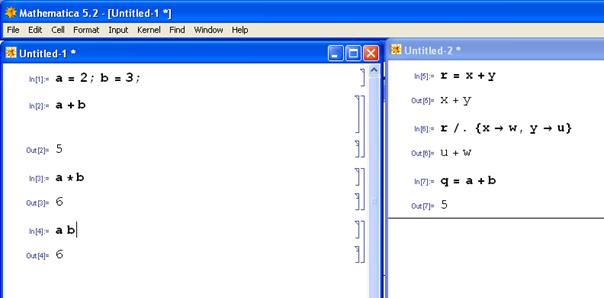
Рис. 3.1. Окно системы Mathematica после запуска, открытия второго окна и выполнения простейших вычислений

А далее, в отличие от MATLAB и подобно Maple, если вы захотите повторить какое-то вычисление, то можно установить курсор вставки в соответствующей строке щелчком и нажать Shift–Enter. Это же можно сделать иначе: установите I-образный курсор на квадратную скобку справа от формулы (курсор при этом изменит свой вид) и щелкните один раз. Скобка «почернеет». Тем самым выделена ячейка, содержащая нужную формулу. Теперь достаточно нажать Shift + Enter. Нужное вычисление будет выполнено. При желании выделенные ячейки можно копировать и размножать обычными для систем с графическим интерфейсом приемами (кнопками или меню). Повторим, все перечисленное является совершенно естественным для пользователя Maple и составляет одно из основных неудобств при его переходе на MATLAB. А вот что очень непривычно для тех, кто привык иметь дело с Maple и является одним из проявлений различий в языках: а) аргументы функций заключаются в квадратные скобки; б) имена функций, встроенных в систему Mathematica, начинаются с заглавных букв.

Как обычно в Windows, для сохранения из меню File выбирается пункт Save As и записывается протокол проведенных расчетов в файл (для Mathematica 5 с расширением.nb – от слова Notebook).

Как видно из рисунка 3.1, арифметические действия в системе Mathematica изображаются обычным образом: +, -, *, ^, но вместо знака умножения можно набирать пробел. Подобно MATLAB и в отличие от Maple, точка с запятой означает команду выполнить оператор и распечатать результат его выполнения, а команда «печатать» – это отсутствие какого-либо знака после оператора.

Внешне отличаются, а по сути применяются точно так же, многие операторы Maple, например evalf: в Mathematica это просто буква N:

N[Pi/2]

1.5708

N[33/7-Sqrt[2]]

3.30007.

Или, например, оператор подстановки (subs в Maple) имеет весьма непривычный и громоздкий вид:

r/.{x®w, y®u}

u+w.

Из следующей строчки проясняется синтаксис этого оператора:

1+x^2+x^4/.x®2

21.

Интересно, что некоторые операторы имеют такой же вид, что и в Maple, но в их действиях есть различия. Например, это относится к simplify: в обеих системах это оператор, упрощающий выражения, но, видимо, понятие «упрощение» создатели двух систем понимают несколько по-разному. Так, в Mathematica разложим степень разности на отдельные слагаемые с помощью оператора Expand, а затем применим к результату Simplify:

q=Expand[(x-y)^3]

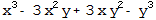
Simplify[q]

.

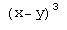А вот что в такой ситуации сделает Maple:

> q: =expand((x-y)^3);

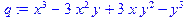
> simplify(q);

.

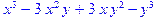Т.е. expand «сработал» так же, а упрощение в Maple понимается как разложение, а в Mathemanica – наоборот, как представление в свернутом виде. Кстати, в Mathematica, помимо обычного Simplify, есть еще «более мощный» оператор FullSimplify. Например, в нижеследующей ситуации Simplify не справляется, а его усиленный аналог – да:

Simplify[Gamma[z] Gamma[1-z]]

Gamma[1-z] Gamma[z]

FullSimplify[Gamma[z] Gamma[1-z]]

p Csc[p z].

Впрочем, в Maple с этой задачей упрощения произведения гамма-функций справится и обычный оператор:

> q: =GAMMA(z)*GAMMA(1-z);

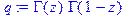
> simplify(q);

.

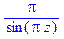Для первичного знакомства с системой, читателю настоятельно рекомендуется проработать все пункты превосходно написанного Tutorial из меню Help в Mathematica. Как неоднократно указывалось, подробное изложение языков и структуры систем выходит за рамки данного пособия. Ограничимся тем, что разберем примеры, решенные выше в Maple и MATLAB.

Функции описываются с помощью знака: =

a=2; f[x_]: =Sin[a*x]/x; g[y_]: =Sin[b*y]

f[1]

Sin[2]

g[3]

Sin[3 b].

Причем x_, y_ означают произвольные переменные под именами x, y. Численные значения выражений и подстановка параметров:

N[f[1]]

-0.378401

N[g[3]/.b®Pi/9]

0.909297.

Построение графиков описанных функций:

Plot[{f[x], g[x]/.b®2}, {x, -15, 15}]

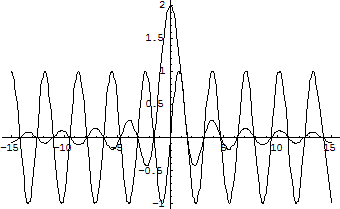
Рис. 3.2. Пример построения графика функций в Mathematica

Построим график функции sin(x+y):

Plot3D[S in[x+y], { x, -2, 2 }, { y, -2, 2 }].

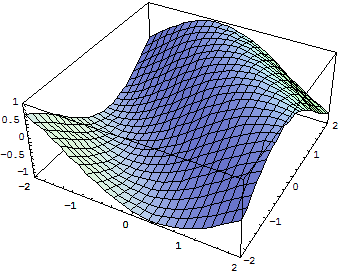
Рис. 3.3. Пример построения графика функции от двух переменных

Решим задачу (1.1) о нахождении емкости трех последовательно включенных емкостей (конденсаторов) C₁, C₂ и C₃ произвольной величины, разобранную в Maple и MATLAB.

eq=1/C0==1/C1+1/C2+1/C3; r=Solve[eq, C0]

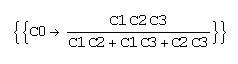
r/.{C1®2, C2®1, C3®4}

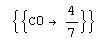
N[r/.{C1®2, C2®1, C3®4}]

{{C0®0.571429}}

Операцию присваивания полученных в процедуре решения функции (в данном случае одной – C0) можно провести следующим образом:

C0=C0/.r

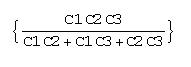
s=C0/.{C1®2, C2®1, C3®4}

.

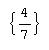Видно, что теперь С₀ определена как функция трех переменных. Результат подстановки в нее значений емкостей 2, 1 и 4 обозначен как s. С ним можно производить действия:

N[s]+1

{1.57143}

Вычисление производных и интегралов:

D[Sin[x]^2+Cos[x]^3, x]

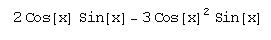
Integrate[Sin[x], x]

-Cos[x]

Integrate[Sin[x], {x, 0, Pi}]

2.

Неберущиеся интегралы в численном виде:

q1=Integrate[Exp[-x^2], {x, -1, 1}]

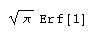
q2=Integrate[Exp[-x^3], {x, -1, 1}]

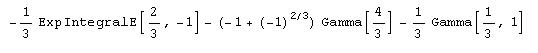
N[q1]

1.49365

N[q2]

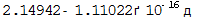
Интересно отметить, что в случае интеграла q2, в отличие от Maple и MATLAB, система Mathematica пыталась как-то вычислить его, преобразовав к сумме гамма-функций и интегральной экспоненты.