Вычисление статистической суммы модели Изинга и сравнение с известными точными выражениями

В качестве еще одного примера применения численно-аналитических пакетов компьютерной алгебры для вычисления сложных систем рассмотрим модель Изинга. Это определенная модель двумерной решетки, для которой точное выражение для статистической суммы и задача о фазовом переходе была впервые решена Л. Онсагером в 1944 г. [4, с. 541–549]. Этот результат часто называют одним из самых выдающихся достижений теоретической физики в 20 веке.

Рассматриваемая модель представляет собой плоскую квадратную решетку, состоящую из N узлов (, где L – сторона квадрата), в каждом из которых находится «спин», с осью, перпендикулярной к плоскости решетки. Спин может иметь две противоположные ориентации, так что общее число всевозможных конфигураций спинов в решетке равно 2^N.

Для описания различных конфигураций поступают следующим образом. С каждым узлом решетки (с координатами k, l) свяжем переменную 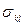, принимающие два значения 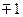, соответствующие двум возможным ориентациям спина. Если ограничиться только учетом взаимодействия между соседними спинами, то энергия конфигурации может быть записана в виде:

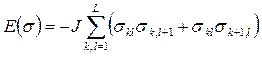. (4.7)

Здесь параметр J определяет энергию взаимодействия пары соседних спинов, равную – J и + J соответственно для одинаковых и противоположных ориентаций спинов.

Основная задача состоит в вычислении статистической суммы

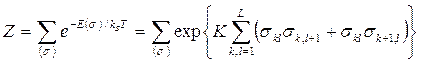, (4.8)

где 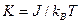, k_B – постоянная Больцмана.

Несмотря на кажущуюся простоту, в случае размерности больше единицы, задача относится к числу сложнейших и показывает, что сложная для вычислений система может возникнуть в относительно простой исходной ситуации. Знаменитое решение Онсагера является не вполне точным, а асимптотическим выражением, справедливым в пределе больших N (т.е. для бесконечной решетки). Оно имеет вид

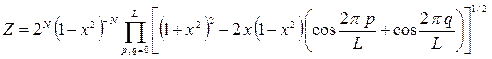, (4.9)

где .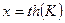

Что касается действительно точного выражения, справедливого для конечной решетки, то оно также было получено Онсагером совместно с Кауфман, и называется решением Кауфман [5, 6]. Однако в отличие от (4.9) для конечного случая требуется задание конкретных граничных условий. Обычно используют так называемые циклические граничные условия, когда крайние (справа – слева и вверху – внизу) спины предполагаются взаимодействующими друг с другом. Пример решетки с N=16 показан на рисунке 4.3.

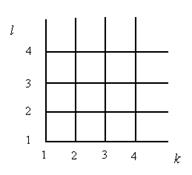
Рис. 4.3.Квадратная решетка спинов размера 4 x 4 (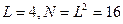) с циклическими граничными условиями

В этом случае точное выражение для статистической суммы, полученное Кауфман, имеет вид суммы четырех слагаемых:

;

;

;

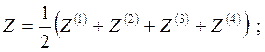
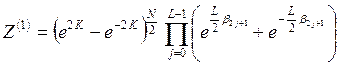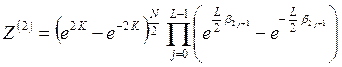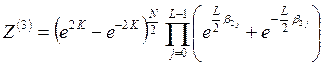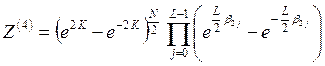, (4.10)

где параметры 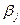являются решениями уравнений: при

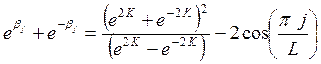(4.11)

и при

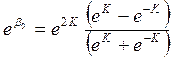. (4.12)

Задачей данной лекции является демонстрация того, как с помощью системы компьютерной алгебры можно как непосредственно рассчитать статистическую сумму модели Изинга двумерной квадратной решетки, так и по формулам (4.10) – (4.12) и, сравнив полученные выражения, убедиться в справедливости решения Кауфман (разумеется, лишь для нескольких небольших значений L). Кроме того, также для нескольких L вычислим точные выражения для статистической суммы в случае наличия внешнего магнитного поля. Как известно, задача Изинга на простой квадратной решетке в магнитном поле до сих пор не решена, так что сравнивать с точным выражением, подобно (4.10) – (4.12), будет невозможно. Здесь мы соприкасаемся с нерешенной проблемой, находящейся на переднем крае исследований.

Но прежде, следуя принятому в данном курсе принципу «от простого к сложному», разберем более простой случай одномерной задачи Изинга. Она решена точно как в отсутствие, так и в присутствии магнитного поля. Статистическая сумма имеет вид

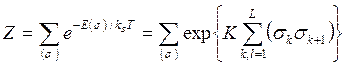, (4.13)

причем согласно циклическому граничному условию 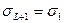. Статистическая сумма при наличии магнитного поля:

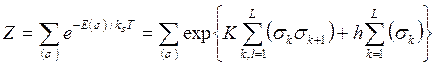, (4.14)

где 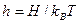, H – напряженность магнитного поля, k_B – постоянная Больцмана.

Точное выражение для статистической суммы (4.14) может быть вычислено достаточно просто и имеет вид

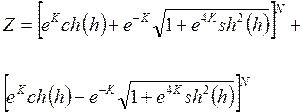(4.15)

При отсутствии магнитного поля, полагая в (4.15) h=0, имеем:

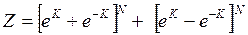. (4.16)

В начале программы зададим длину цепочки спинов (начнем с наименьшего N=2) и вычислим выражение (4.16):

> restart:

> N: =2:

> Z: =(exp(K)+exp(-K))^N+(exp(K)-exp(-K))^N;

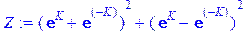
Далее вычислим (4.13):

> S: =sum(sum(product(abs(sigma[m]), m=1..N)*exp(K)^(sum(sigma[k]*sigma[k+1], k=1..N-1)+sigma[N]*sigma[1]), sigma[1]=-1..1),

sigma[2]=-1..1);

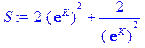
В этом выражении искусственно введено произведение абсолютных величин sigma[1] и sigma[2] для того, чтобы исключить из сумм те слагаемые, в которых хотя бы одна из sigma[1], sigma[2] равна нулю, чтобы можно было использовать диапазон суммирования – 1..1. Он включает в себя – 1, 0, 1, а нужно только – 1, 1. Итак, под именем Z у нас точное выражение (4.16), а под именем S – непосредственно вычисленное по (4.13). Сравним их:

> simplify(S-Z);

.

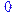Они совпадают, следовательно, (4.16) является правильным выражением в случае N=2. Можно проверить и для других значений N, но тогда надо не только переопределить N, но также добавить дополнительные суммирования в операторе, вычисляющем статистическую сумму по (4.13). Например, для N=3:

> restart:

> N: =3:

> Z: =(exp(K)+exp(-K))^N+(exp(K)-exp(-K))^N;

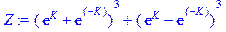
> S: =sum(sum(sum(product(abs(sigma[m]), m=1..N)*exp(K)^(sum(sigma[k]*sigma[k+1], k=1..N-1)+sigma[N]*sigma[1]), sigma[1]=-1..1), sigma[2]=-1..1), sigma[3]=-1..1);

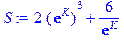
> simplify(S-Z);

.

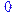Теперь можно сделать шаг вперед и проверим выражение (4.15), сравнив его с (4.14). Сделаем это для N=4.

> restart:

> N: =4:

> Z: =(exp(K)*(exp(h)+exp(-h))/2+exp(-K)*sqrt(1+exp(4*K)*((exp(h)-exp(-h))/2)^2))^N+(exp(K)*(exp(h)+exp(-h))/2-exp(-K)*sqrt(1+exp(4*K)*((exp(h)-exp(-h))/2)^2))^N;

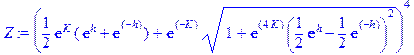
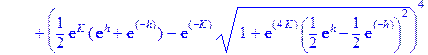
> S: =sum(sum(sum(sum(product(abs(sigma[m]), m=1..N)*exp(K)^(sum(sigma[k]*sigma[k+1], k=1..N-1)+sigma[N]*sigma[1])*exp(h)^sum(sigma[r], r=1..N), sigma[1]=-1..1), sigma[2]=-1..1), sigma[3]=-1..1), sigma[4]=-1..1);

> simplify(S-Z);

.

Освоив одномерный случай как в отсутствии, так и в присутствии магнитного поля и имея полную уверенность в том, что наша программа правильно работает в этом случае, можно обобщить ее на двумерную квадратную решетку. Непосредственно вычисляем статистическую сумму по формуле (4.8) и сравниваем с решением Кауфман (4.10) – (4.12). Начнем с наименьшей решетки L=2, т.е. размера 2 x 2.

> restart: with(linalg):

> L: =2:

> for j from 1 to 2*L-1 do beta_[j]: =arccosh((ek^2+1/ek^2)^2/(ek^2-1/ek^2)/2-cos(Pi*j/L)): od:

> beta_[0]: =ln(ek^2*(sqrt(ek^2)-1/sqrt(ek^2))/(sqrt(ek^2)+1/sqrt(ek^2))):

> c: =(ek^2-1/ek^2)^(L^2/2):

Здесь вычислили величины по формулам (4.11), (4.12). Обратим внимание, что (4.11) было решено относительно , используя обратную гиперболическую функцию arccosh. Кроме того, здесь вместо exp(K), используем символ ek. Это сделано для ускорения расчетов, поскольку при больших размерностях использование явного выражения exp(K) заставляет программу проводить слишком громоздкие преобразования. Получив результаты, зависящие от ek, всегда можно с помощью оператора subs подставить явное выражение. Такой прием часто может оказаться весьма полезным. Разумеется, такого рода трудности выясняются на практике, при попытках вычислить сначала обычным образом.

Далее вычисляем слагаемые формулы (4.10) и всю сумму:

> z1: =c*product(exp(L*beta_[2*j1+1]/2)+1/exp(L*beta_[2*j1+1]/2), j1=0..L-1):

> z2: =c*product(exp(L*beta_[2*j2+1]/2)-1/exp(L*beta_[2*j2+1]/2), j2=0..L-1):

> z3: =c*product(exp(L*beta_[2*j3]/2)+1/exp(L*beta_[2*j3]/2), j3=0..L-1):

> z4: =c*product(exp(L*beta_[2*j4]/2)-1/exp(L*beta_[2*j4]/2), j4=0..L-1):

> a1: =simplify(z1, symbolic): a2: =simplify(z2, symbolic): a3: =simplify(z3, symbolic): a4: =simplify(z4, symbolic):

> Z: =simplify(a1+a2+a3+a4)/2;

.

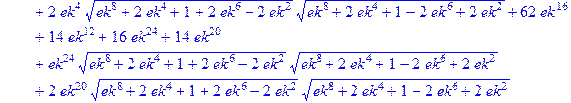
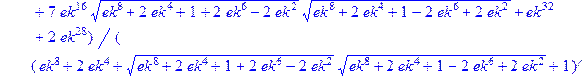
Для непосредственного вычисления статистической суммы (4.8) за основу можно взять соответствующий оператор из программы для одномерной модели:

> S: =sum(sum(sum(sum(product(product(abs(sigma[m, n]), m=1..L), n=1..L)*ek^(sum(sum(sigma[k, l]*sigma[k, l+1]+

sigma[k, l]*sigma[k+1, l], k=1..L-1), l=1..L-1)+ sum(sigma[L, l]*sigma[L, l+1]+sigma[L, l]*sigma[1, l], l=1..L-1)+sum(sigma[k, L]*sigma[k+1, L]+sigma[k, L]*sigma[k, 1], k=1..L-1)+sigma[L, L]*sigma[L, 1]+sigma[L, L]*sigma[1, L]),

sigma[1, 1]=-1..1), sigma[1, 2]=-1..1), sigma[2, 1]=-1..1), sigma[2, 2]=-1..1);

> simplify(S-Z);

.

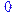Итак, выражения совпали, что говорит о правильности формулы Кауфман для L=2. Аналогично можно проверить для больших размерностей. Так, при L=3 непосредственное вычисление по (4.8) дает:

> L: =3:

> S: =sum(sum(sum(sum(sum(sum(sum(sum(sum(product(product(abs(sigma[m, n]), m=1..L), n=1..L)*ek^ (sum(sum(sigma[k, l]*sigma[k, l+1]+sigma[k, l]*sigma[k+1, l], k=1..L-1), l=1..L-1)+ sum(sigma[L, l]*sigma[L, l+1]

+sigma[L, l]*sigma[1, l], l=1..L-1)+sum(sigma[k, L]*sigma[k+1, L]

+sigma[k, L]*sigma[k, 1], k=1..L-1)+ sigma[L, L]*sigma[L, 1]+sigma[L, L]*sigma[1, L]), sigma[1, 1]=-1..1), sigma[1, 2]=-1..1), sigma[2, 1]=-1..1), sigma[2, 2]=-1..1), sigma[1, 3]=-1..1), sigma[2, 3]=-1..1), sigma[3, 1]=-1..1), sigma[3, 2]=-1..1), sigma[3, 3]=-1..1);

,

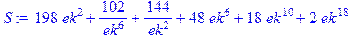а при L=4 (случай решетки, изображенной на рисунке 4.3):

> L: =4:

> S: =sum(sum(sum(sum(sum(sum(sum(sum(sum(sum(sum(sum(sum(sum(sum(sum(product(product(abs(sigma[m, n]), m=1..L), n=1..L)*ek^ (sum(sum(sigma[k, l]*sigma[k, l+1]+sigma[k, l]*sigma[k+1, l], k=1..L-1), l=1..L-1)+ sum(sigma[L, l]*sigma[L, l+1]+sigma[L, l]*sigma[1, l], l=1..L-1)+sum(sigma[k, L]*sigma[k+1, L]+sigma[k, L]*sigma[k, 1], k=1..L-1)+ sigma[L, L]*sigma[L, 1]+sigma[L, L]*sigma[1, L]), sigma[1, 1]=-1..1), sigma[1, 2]=-1..1), sigma[2, 1]=-1..1), sigma[2, 2]=-1..1), sigma[1, 3]=-1..1), sigma[2, 3]=-1..1), sigma[3, 1]=-1..1), sigma[3, 2]=-1..1), sigma[3, 3]=-1..1), sigma[1, 4]=-1..1), sigma[2, 4]=-1..1), sigma[3, 4]=-1..1), sigma[4, 1]=-1..1), sigma[4, 2]=-1..1), sigma[4, 3]=-1..1), sigma[4, 4]=-1..1);

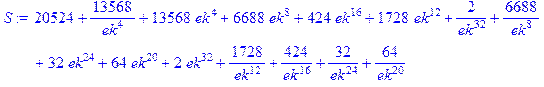
Приведем еще результат для L=5

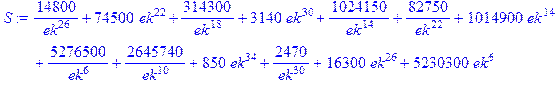
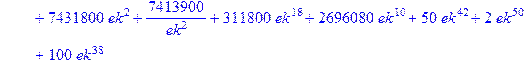
В этих случаях также сравнение с формулой Кауфман дает полное совпадение. Интересно отметить, однако, что с увеличением размерности вычисления по формулам Кауфман (4.10) – (4.12) становятся все более трудоемкими и занимают намного больше времени, чем непосредственное вычисление (4.8)! Впрочем, и последнее становится проблематичным уже при L=7, при использовании компьютера с обычными ресурсами, поскольку тогда общее количество вариантов конфигураций спинов, которые необходимо просуммировать, равно 2⁴⁹.

Построим графики полученных статистических сумм в зависимости от 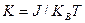(т.е. от обратной температуры). Для этого, как говорилось выше, подставим вместо символического ek явную экспоненту:

> f2: =subs(ek=exp(K), S2); f3: =subs(ek=exp(K), S3); f4: =subs(ek=exp(K), S4): f5: =subs(ek=exp(K), S5):

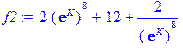
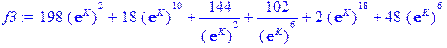
и применим оператор построения графиков, например, для L=3:

> plot({f3}, K=0..0.6);

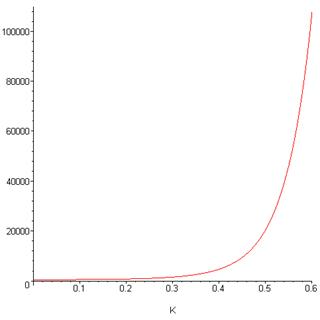
Рис. 4.4.Зависимость точной статистической суммы 3 x 3 квадратной решетки от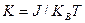

Видно, что статистическая сумма монотонно возрастает и не имеет сингулярностей (можно убедиться в этом, строя график в различных диапазонах). Т.е. фазовый переход в решетке размером 3 x 3 невозможен (что неудивительно для такой малой и простой системы). Как известно из теории модели Изинга [4, с. 548], фазовый переход возможен в случае бесконечной квадратной решетки, т.е. при 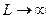. Статистическая сумма в этом случае дается выражением (4.9). Вычислим это выражение для нескольких L и построим графики. Строго говоря, решение Онсагера является асимптотическим и совпадает с реальной статистической суммой лишь в пределе 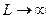, т.е. тем точнее, чем больше L. Тем не менее, формально его можно вычислить даже при L=2.

Воплотим формулу (4.9) в программе, произведем вычисления для значений L от 4 до 18, подставим в полученные выражения вместо 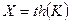и построим графики их логарифмов в зависимости от K. Результат приведен на рисунке 4.5. Видно, что статистические суммы имеют сингулярности в одной и той же точке. На графике верхней кривой L=18 может сложиться впечатление, что сингулярности нет, однако если построить тот же график с «большим разрешением», то можно убедиться, что сингулярность есть, как видно из рисунка 4.6.

> for j from 4 to 18 do L: =j: N: =L^2: Z[j]: =2^N*(1-X^2)^(-N)*product(product(((1+X^2)^2-2*X*(1-X^2)*

(cos(2*Pi*p/L)+cos(2*Pi*q/L)))^(1/2), p=0..L), q=0..L):

Z_[j]: =subs(X=tanh(K), Z[j]): od:

> plot({ln(Z_[4]), ln(Z_[5]), ln(Z_[6]), ln(Z_[7]), ln(Z_[8]), ln(Z_[9]), ln(Z_[10]), ln(Z_[11]), ln(Z_[12]), ln(Z_[13]), ln(Z_[14]), ln(Z_[15]), ln(Z_[16]), ln(Z_[17]), ln(Z_[18])}, K=0..1.2);

Положение сингулярности согласуется со значением 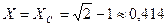, известным из литературы [4, с. 548].

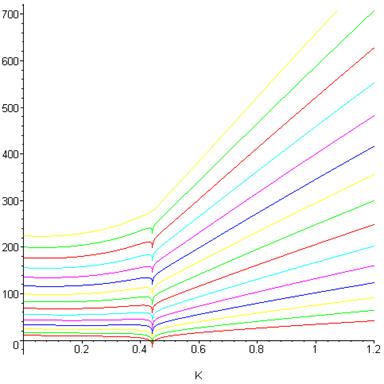
Рис. 4.5. Зависимость от логарифма статистической суммы квадратной решетки по формуле Онсагера (4.9), для L от 4 (нижняя кривая) до 18 (верхняя кривая)

> plot({ln(Z_[18])}, K=0.4..0.6);

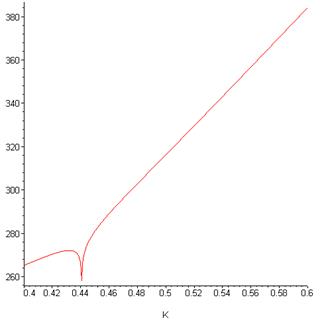
Рис. 4.6. Логарифм статистической суммы для L =4 квадратной решетки, полученный по формуле Онсагера (4.9) вблизи сингулярности

Как уже неоднократно указывалось, формула Онсагера (4.9) неправильно описывает статистическую сумму для решеток малых размеров. Построим на одном графике соответствующие кривые, чтобы наглядно увидеть, в чем состоит расхождение.

> plot({ln(Z_[4]), ln(f4), ln(Z_[5]), ln(f5)}, K=0..4);

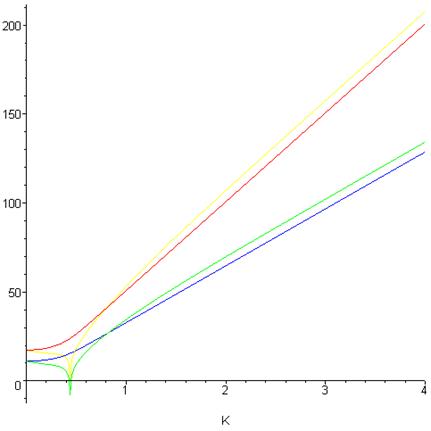
Рис. 4.7.Логарифм статсуммы для L =4 (внизу) и L =5 (вверху) квадратной решетки, вычисленный по формуле Онсагера (4.9) и точные результаты

Видно, что расхождение существенное, причем кривые качественно различны при малых K, т.е. при высоких температурах (вспомним, что 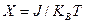). При больших K (низких температурах) расхождение несущественно. Программа компьютерной алгебры позволяет просматривать полученные функции с разной степенью разрешения:

> plot({ln(Z_[5]), ln(f5)}, K=9..10);

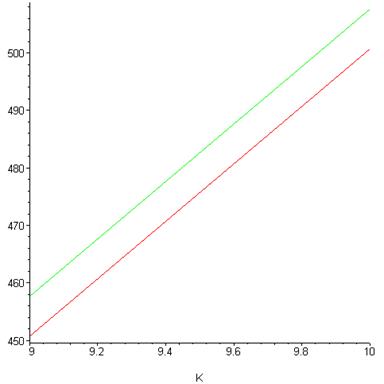
Рис. 4.8.Логарифмы статистической суммы для квадратной решетки размера L =5, вычисленные по формуле Онсагера (4.9) (верхняя кривая), и точный результат для низких температур

Наконец, применим нашу программу для вычисления статистической суммы квадратной решетки во внешнем магнитном поле. Как указывалось, это является одной из важнейших нерешенных проблем теоретической физики. Сделать это мы сможем, разумеется, лишь для самых малых размеров решетки. Нижеследующая программа вычисляет такую статсумму для решетки размера 3 x 3. Обратите внимание, что единственное отличие от программы без магнитного поля выделено более крупным шрифтом.

> restart: L: =2:

> S2: =sum(sum(sum(sum(product(product(abs(sigma[m, n]), m=1..L), n=1..L)*ek^(sum(sum(sigma[k, l]*sigma[k, l+1]+

sigma[k, l]*sigma[k+1, l], k=1..L-1), l=1..L-1)+ sum(sigma[L, l]*sigma[L, l+1]+sigma[L, l]*sigma[1, l], l=1..L-1)+sum(sigma[k, L]*sigma[k+1, L]+sigma[k, L]*sigma[k, 1], k=1..L-1)+sigma[L, L]*sigma[L, 1]+sigma[L, L]*sigma[1, L]) *eh^(sum(sum(sigma[k, l], k=1..L), l=1..L)), sigma[1, 1]=-1..1), sigma[1, 2]=-1..1), sigma[2, 1]=-1..1), sigma[2, 2]=-1..1);

.

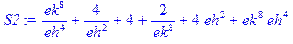Подставим вместо символических ek, eh явные выражения:

> f2: =subs({ek=exp(K), eh=exp(h)}, S2);

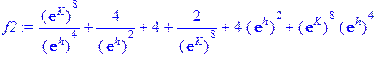
и построим график от двух переменных:

> plot3d(ln(f2), K=0..1.4, h=0..2);

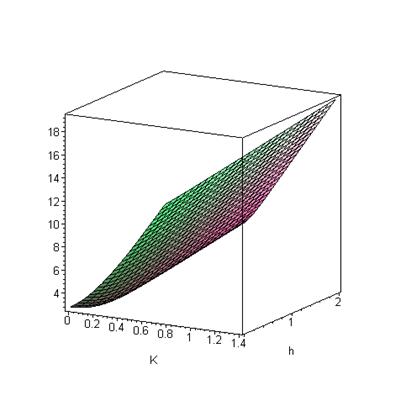
Рис. 4.9. Логарифм статистической суммы для квадратной решеткиразмера L =5 внешним магнитным полем H (здесь h=H/k_BT)

Аналогично для L=3 вычисления дают:

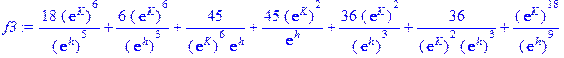
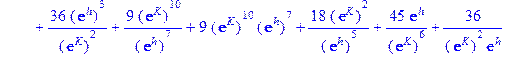
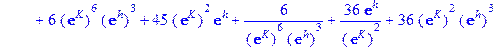
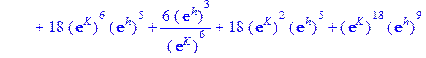
Можно вычислить так называемую спонтанную намагниченность, которую для модели Изинга обычно оценивают по формуле:

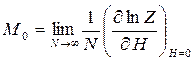(4.17)

Нам недоступно выражение при больших N, поэтому оценим спонтанную намагниченность для конечных случаев L=2; 3:

> evalf(subs(h=0, diff(ln(f2), h))); evalf(subs(h=0, diff(ln(f3), h)));

Таким образом, для конечных решеток с L=2; 3 спонтанная намагниченность отсутствует.

Можно обобщить программу для вычисления еще более интересного случая трехмерной модели Изинга, что будет проведено в лабораторной работе.