
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тема 4. Примеры вычислений и моделирования систем с помощью численно-аналитических пакетов программ
|
|
4.1. Имитационное моделирование методом Монте-Карло модельной системы броуновского движения: случайные блуждания на прямой
Броуновское движение является типичным примером так называемой стохастической системы. Это явление было открыто в 1827 году английским ботаником Брауном (1773–1858). Это движение тем оживлённее, чем выше температура и чем меньше вязкость среды. Его едва удаётся обнаружить в глицерине, а в газах оно, напротив, чрезвычайно интенсивно. Оно представляет собой хаотичное движение достаточно крупной (по сравнению с молекулами и видимой под микроскопом) частицы, находящейся в жидкой среде, происходящее под действием случайных ударов по ней со стороны молекул. Последние находятся в состоянии теплового движения с характерной скоростью 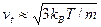 , где kB – постоянная Больцмана, T – температура среды в абсолютной шкале, m – масса молекулы. Направление движения молекулы и момент ее столкновения с броуновской частицей являются случайными величинами. Иными словами, в каждый момент времени неизвестно, столкнется ли с ней молекула, а если столкнется, то неизвестно, с какой стороны она «ударит». Вообще говоря, неизвестно и точное значение величины скорости молекулы. Тем не менее, можно оценить параметры вероятностных распределений этих величин. Например, в отношении направления скорости молекулы чаще всего обоснованным является предположение о равновероятном (равномерном) распределении. Частота столкновения молекул с частицей зависит от их концентрации (т.е. от плотности среды), от их скоростей и от геометрического размера частицы. Что касается величины скорости, то хорошим приближением часто является распределение Максвелла, т.е. нормальное распределение с дисперсией, определяемой температурой среды. Но можно и предположить, что все скорости одинаковы и равны
, где kB – постоянная Больцмана, T – температура среды в абсолютной шкале, m – масса молекулы. Направление движения молекулы и момент ее столкновения с броуновской частицей являются случайными величинами. Иными словами, в каждый момент времени неизвестно, столкнется ли с ней молекула, а если столкнется, то неизвестно, с какой стороны она «ударит». Вообще говоря, неизвестно и точное значение величины скорости молекулы. Тем не менее, можно оценить параметры вероятностных распределений этих величин. Например, в отношении направления скорости молекулы чаще всего обоснованным является предположение о равновероятном (равномерном) распределении. Частота столкновения молекул с частицей зависит от их концентрации (т.е. от плотности среды), от их скоростей и от геометрического размера частицы. Что касается величины скорости, то хорошим приближением часто является распределение Максвелла, т.е. нормальное распределение с дисперсией, определяемой температурой среды. Но можно и предположить, что все скорости одинаковы и равны 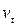 .
.
Рассмотрим предельно простую модель, когда частица может двигаться только вдоль прямой, и она испытывает столкновения со стороны молекул справа или слева. Можно возразить, что эта одномерная модель слишком примитивна и имеет мало отношения к действительности. Однако не надо забывать, что нашей целью является моделирование, которое включает в себя собственно составление модели и реализацию ее в виде компьютерной программы. Следовательно, если вы составите сразу предельно реалистичную, а, следовательно, сложную модель, то вам придется сразу составлять и сложную программу. На этом двухступенчатом пути в таком случае вы с большой вероятностью совершите ошибку, или же столкнетесь с проблемой, которую не сможете решить или потратите неоправданно много времени на ее решение. Поэтому правильным подходом является такой: сначала составляете простую, пусть даже далекую от реальности, модель. Программная реализация этой модели будет, тем не менее, содержать достаточно много из того, что сохранится и в дальнейшем. Далее надо определить, в каких аспектах ваша простая модель далека от реальности, и составить другую, более реалистичную модель. Вам будет неизмеримо проще внести изменения в программу, чтобы приспособить ее к новой модели, чем сразу «с нуля» составлять программу для сложной модели.
Более того, часто оказывается, что выводы, сделанные на основе простой модели, сами по себе оказываются весьма реалистичными и объясняют сущность явления.
Итак, упрощенная одномерная модель броуновского движения, или модель случайных блужданий вдоль прямой, включает в себя следующее. Частица (материальная точка) массы M испытывает столкновения со стороны молекул (других материальных точек) массы m (ясно, что 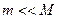 ). В каждый момент времени столкновение может произойти с вероятностью p, причем если столкновение произойдет, то с равной вероятностью оно будет справа или слева. Скорость молекулы равна u. Столкновения молекул с частицей упругие. При отсутствии столкновений частица свободно движется вдоль прямой, т.е. на нее не действуют никакие силы. Нас интересует координата частицы в зависимости от времени и вычисление среднего по времени отклонения частицы от начала координат.
). В каждый момент времени столкновение может произойти с вероятностью p, причем если столкновение произойдет, то с равной вероятностью оно будет справа или слева. Скорость молекулы равна u. Столкновения молекул с частицей упругие. При отсутствии столкновений частица свободно движется вдоль прямой, т.е. на нее не действуют никакие силы. Нас интересует координата частицы в зависимости от времени и вычисление среднего по времени отклонения частицы от начала координат.
В принципе, в вышеприведенном абзаце приведено полное описание модели. Однако прежде чем составлять программу, необходимо выполнить еще один этап: разобраться в физических процессах, которые протекают в модели, написать соответствующие формулы и уравнения и продумать, как эти процессы будут воплощены в программе. Важно понимать, что ни один самый совершенный программный пакет на это не способен, это под силу только живому разуму.
В данном случае основной физический процесс, определяющий поведение нашей модели, представляет собой упругое столкновение двух тел. Масса первого тела M, его скорость до столкновения обозначим V, масса второго тела m, скорость до столкновения u. После столкновения скорости 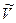 и
и 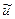 (в программе будем обозначать Vt и ut). Все эти скорости могут иметь положительные и отрицательные значения, причем положительное значение соответствует движению слева направо вдоль оси, а отрицательное – справа налево. Необходимо найти скорости после столкновения, т.е. выразить их через скорости до него. Из механики известно, что это проще сделать, используя законы сохранения энергии и импульса:
(в программе будем обозначать Vt и ut). Все эти скорости могут иметь положительные и отрицательные значения, причем положительное значение соответствует движению слева направо вдоль оси, а отрицательное – справа налево. Необходимо найти скорости после столкновения, т.е. выразить их через скорости до него. Из механики известно, что это проще сделать, используя законы сохранения энергии и импульса:
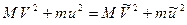 ;
;
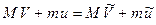 . (4.1)
. (4.1)
Уравнения (4.1) простые и могут быть решены относительно 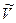 и
и 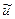 непосредственно. Однако для их решения также применим Maple:
непосредственно. Однако для их решения также применим Maple:
> restart:
> assume(M> 0, m> 0):
> eq1: =M*V^2+m*u^2=M*Vt^2+m*ut^2; eq2: =M*V+m*u=M*Vt+m*ut;
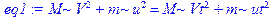
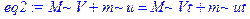
> R: =solve({eq1, eq2}, {ut, Vt});
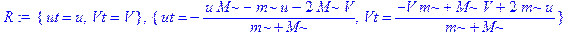 .
.
Нас интересует значение скорости частицы после столкновения, скорость молекулы 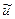 никакого интереса не представляет. Итак, получено, что
никакого интереса не представляет. Итак, получено, что
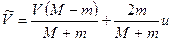 . (4.2)
. (4.2)
Формулу (4.2) можно преобразовать с целью выделить отношение 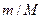 , которое в силу того, что
, которое в силу того, что 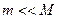 является малым, и по нему можно разложить:
является малым, и по нему можно разложить:
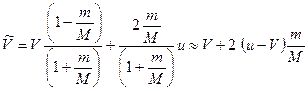 (4.3)
(4.3)
(ограничились линейными по 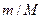 членами).
членами).
В реальности m значительно меньше M, так что имеет смысл использовать упрощенный вариант формулы (4.3). Однако для составляемой учебной программы это не имеет значения, поскольку и точная формула достаточно проста и позволит провести вычисления в случае, если число шагов не будет слишком велико. В случае большого числа шагов выбор более простой, но физически обоснованной формулы может иметь решающее значение для практической выполнимости вычислений. Имеет смысл делать прикидки быстродействия различных вариантов, используя ту же программу, в которой будут производиться расчеты. Например, в Maple в правой нижней части командного окна имеется счетчик времени. Проведем эксперимент: выполним простые, но многократные вычисления по двум вариантам формулы, например, присваивание значений некоторому массиву для достаточно большого числа значений. Первый вариант (по точному варианту формулы):
> M: =100: m: =1: u: =10:
> for j from 1 to 200000 do t[j]: =j*(1-m/M)/(1+m/M)+2*(m/M)*u/(1+m/M): od:
Второй вариант (по приближенному варианту):
> M: =100: m: =1: u: =10:
> for j from 1 to 200000 do t[j]: =j+2*(u-j)*(m/M): od:
Время выполнения этих программ с 200000 шагами каждая: первой – 6, 4 секунды, второй – 2, 2 секунды. Различие очень существенное, так что если масса молекулы действительно намного меньше массы частицы, лучше использовать более простую приближенную формулу.
Поскольку модель вероятностная, программа будет включать в себя использование случайных чисел для моделирования вероятностных распределений. Генераторы случайных (точнее, псевдослучайных) чисел имеются во всех без исключения численных и численно-аналитических программах. Разобраться в способах использования этих генераторов не составляет труда, вызывая соответствующие разделы Help. Так, в Maple можно описать процедуру генерирования (целых) случайных чисел в заданном диапазоне (например, от 1 до 100):
> restart:
> q: =rand(1..100);
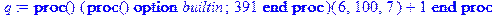
> q(); q(); q(); q();
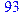
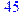

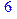 .
.
Как видим, вызов процедуры производится с помощью оператора имя процедуры(). Однако есть одно, но очень существенное «но». Попробуйте выполнить ту же программу, начиная с restart, потом еще и еще раз. Можно заметить, что генерируются в точности одни и те же, якобы «случайные», числа! Ясно, что так использовать генератор случайных чисел в составе моделирующей программы нельзя, т.к. при различных «прогонах» («runs» в англоязычной литературе) будут получаться одинаковые результаты и никакого усреднения не получится. Это является проявлением того, что генерируются не истинно случайные (в компьютере это невозможно), а псевдослучайные числа. Они представляют собой результат вычисления по некоторому, вполне определенному, но очень запутанному алгоритму. Т.е. оказывается, что случайные числа, необходимые для моделирования, сами представляют собой результат некоторого моделирования!
Выход заключается в том, что указанный алгоритм генерирования псевдослучайных чисел можно запускать, начиная с разных моментов, и этот стартовый момент можно связать, например, с текущим показанием часов компьютера. Это делается с помощью оператора randomize(), который в вышеприведенной программе надо выполнить между restart и q=rand(1..100);. Читателю предоставляется возможность проверить, что тогда при различных прогонах, начиная с randomize(), генерируются разные числа. Эта процедура называется «посев» последовательности псевдослучайных чисел (seed по-английски).
Приступим к составлению программы. Вначале, помимо randomize, загрузим библиотеку stats (вычисления статистических характеристик) с помощью оператора with. Зададим значения параметров модели 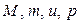 . Зададим T – количество элементарных временных шагов, т.е. общее время, в течение которого будет функционировать модель. Вычислим и сохраним под некоторыми именами те части формулы (4.2), которые не будут изменяться со временем:
. Зададим T – количество элементарных временных шагов, т.е. общее время, в течение которого будет функционировать модель. Вычислим и сохраним под некоторыми именами те части формулы (4.2), которые не будут изменяться со временем: 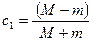 и
и 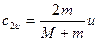 . Единственная величина в (4.2), которая изменяется со временем – это скорость частицы, ввиду постоянных ударов со стороны молекул, передающих частице свой импульс. Кроме того, зададим две процедуры генерирования случайных чисел: одно в интервале от 1 до 100, другое – бинарное (1 или 2).
. Единственная величина в (4.2), которая изменяется со временем – это скорость частицы, ввиду постоянных ударов со стороны молекул, передающих частице свой импульс. Кроме того, зададим две процедуры генерирования случайных чисел: одно в интервале от 1 до 100, другое – бинарное (1 или 2).
> restart:
> with(stats): randomize():
> T: =1000:
> M: =100: m: =1: u: =10: p: =0.75:
> c1: =(M-m)/(M+m): c2u: =u*2*m/(M+m):
> ra: =rand(1..100): roll_1: = rand(1..2):
Основными динамическими величинами в нашей модели являются две: координата частицы X и ее скорость V. Моделирование заключается в том, чтобы вычислить значения координаты и скорости в каждый из T моментов времени. Таким образом, X и V представляют собой массивы длиной T. Опишем их как векторы. В начальный момент положим координату и скорость равными нулю, кроме того, на всякий случай занулим вначале и все остальные элементы массивов:
> X: =vector(T): V: =vector(T):
> for k from 1 to T do V[k]: =0: X[k]: =0: od:
Согласно динамическим законам, координата и скорость в момент времени t определяются значениями координаты и скорости в предшествующий момент времени. Если интервал времени между последовательными моментами равен Δ t, тогда имеем из кинематики
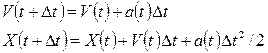 (4.4)
(4.4)
Необходимо как-то конкретизировать Δ t. Будем считать, что этот элементарный промежуток времени достаточно мал, но при этом он значительно больше, чем характерное время взаимодействия (столкновения) молекулы и частицы. Такого рода предположение о малом промежутке времени или расстоянии/объеме является стандартным в статистической и молекулярной физике. Поэтому вместо первого уравнения (4.4) будем предполагать, что скорость 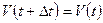 , т.е. не меняется, но в случае, если происходит столкновение с молекулой, скорость частицы мгновенно меняется на новое значение (4.3). Что касается второго уравнения (4.4), то по той же причине (мгновенность взаимодействия, т.е. мгновенность действия ускорения a) в нем не будет последнего слагаемого.
, т.е. не меняется, но в случае, если происходит столкновение с молекулой, скорость частицы мгновенно меняется на новое значение (4.3). Что касается второго уравнения (4.4), то по той же причине (мгновенность взаимодействия, т.е. мгновенность действия ускорения a) в нем не будет последнего слагаемого.
Для удобства положим Δ t=1, это означает, что время в нашей модели будет измеряться в единицах Δ t. Теперь все готово для запуска основной части нашей программы: цикл по времени от 1 до T, на каждом шаге которого будет осуществляться расчет очередных значений массивов X и V на основе предыдущих значений. При этом на каждом шаге с помощью случайных чисел решатся два вопроса: а) будет ли на этом шаге столкновение с молекулой; б) если будет, то где – справа или слева; вот для чего нам понадобится две последовательности случайных чисел.
> for j from 1 to T-1 do X[j+1]: =evalf(X[j]+V[j]): if(ra()/100< p) then if(roll_1()=1) then V[j+1]: =V[j]*c1+c2u: else V[j+1]: =V[j]*c1-c2u: fi else V[j+1]: =V[j]: fi: od:
Надо помнить, что весь этот текст написан в одном командном поле программы (выполняется одним нажатием Enter). Разделение по строкам сделано искусственно с помощью клавиши пробела для большей наглядности и понимания структуры программы. Сделаем несколько пояснений. Оператор X[j+1]: =evalf(X[j]+V[j]): вычисляетновое значение координаты по второму уравнению (4.4) без последнего члена. Далее используется случайное целое число ra, которое ранее было нормировано на диапазон от 0 до 100. Но поскольку вероятность столкновения с молекулой p у нас задается в долях единицы, то случайное число используется в виде ra/100, т.е. нормируется от 0 до 1. Имеем два вложенных друг в друга оператора if: внешний сравнивает вероятность столкновения p с ra/100, и если окажется, что 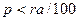 , это означает, что столкновение с молекулой произойдет. Тогда выполняется второй (внутренний) оператор if, в котором решается («разыгрывается»), с какой стороны оно произойдет: если случайное число roll_1=1, то считаем, что молекула «ударила» слева, что соответствует положительному знаку ее скорости u. В противном случае (roll_1=2) знак скорости молекулы будет отрицательным, т.е. она столкнется с частицей справа. В обоих случаях во внутреннем операторе if используется точный вариант формулы (4.3), но с разными знаками u.
, это означает, что столкновение с молекулой произойдет. Тогда выполняется второй (внутренний) оператор if, в котором решается («разыгрывается»), с какой стороны оно произойдет: если случайное число roll_1=1, то считаем, что молекула «ударила» слева, что соответствует положительному знаку ее скорости u. В противном случае (roll_1=2) знак скорости молекулы будет отрицательным, т.е. она столкнется с частицей справа. В обоих случаях во внутреннем операторе if используется точный вариант формулы (4.3), но с разными знаками u.
Если же окажется, что 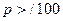 , то столкновения на данном шаге не будет, и выполняется опция else внешнего оператора if: V[j+1]: =V[j]:, т.е. скорость остается без изменения.
, то столкновения на данном шаге не будет, и выполняется опция else внешнего оператора if: V[j+1]: =V[j]:, т.е. скорость остается без изменения.
Если основной цикл выполнен без сбоев, это означает, что массивы X и V получены. Для наглядной визуализации построим их графики. Впрочем, для броуновской частицы интерес представляет только ее координата. Для построения точечного графика (т.е. графика по отдельным заданным точкам) в Maple необходимо представить данные в формате «список данных» (list). Формат «vector», в котором у нас представлен массив X, не будет принят оператором построения графиков plot (убедитесь в этом). Создадим массив под именем X_ в виде двойного списка аргумент–значение функции:
> X_: =[[n, X[n]] $n=1..T]:
Эквивалентная форма (seq – от sequence – последовательность):
> X_p: = {seq([t, X[t]], t=1..T)}:
Вот что представляют собой элементы X_:
> X_[1]; X_[10];
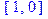
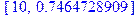 .
.
Теперь можно применить plot:
> plot(X_, x=1..T, style=point, symbol=circle);
Впрочем, можно построить точечный график, используя специально предназначенный для этого оператор pointplot, входящий в состав графической библиотеки plots (которую необходимо загрузить оператором with). Формат, приемлемый для него, – тот же самый двойной список.
> with(plots);
> pointplot(X_);
В результате получаем график координаты частицы в зависимости от времени, т.е. «историю» ее случайных блужданий при данном прогоне программы. Можно повторить программу, начиная или с restart или с randomize, тогда получим другие результаты. На рисунке 4.1 показано несколько получившихся графиков.
Несмотря на то, что для броуновской частицы интерес представляет только ее координата, для исследования самой модели и анализа ее адекватности, построим также график массива скорости частицы V:
> V_: =[[n, V[n]] $n=1..T]:
> plot(V_, x=1..T, style=line);
Типичный график показан на рисунке 4.2.
Из графика видно, что скорость частицы является негладкой (не дифференцируемой) функцией. Этого и следовало ожидать, исходя из предположения, заложенного в модель, о мгновенном характере изменения скорости при ударе со стороны молекулы.
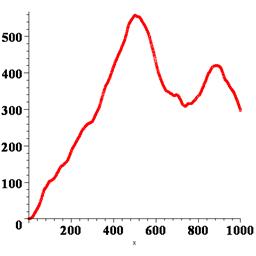
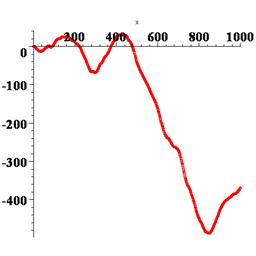
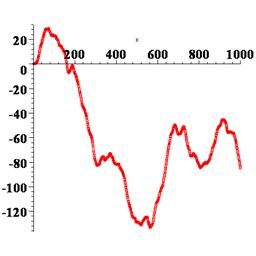

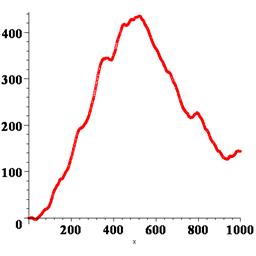
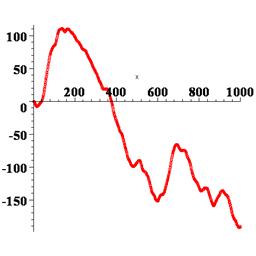
Рис. 4.1. Изменения во времени координаты одномерного движения броуновской частицы, полученные при различных прогонах программы
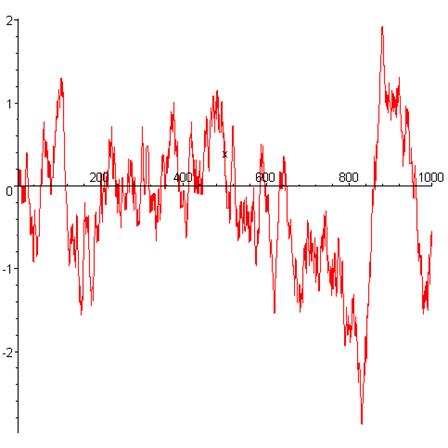
Рис. 4.2. Изменение скорости одномерного движения броуновской частицы
Здесь настает момент, когда необходимо остановиться и задаться вопросом: что, собственно говоря, сделано и с какой целью, т.е. что полезного из всего этого можно извлечь? Имеет ли смысл получать различные графики, подобные изображенным на рисунке 4.1 и анализировать их? Например, при первом прогоне, как видно из рисунке 4.1, график имеет восходящий тренд, это означает, что частица двигалась в сторону положительных значений координаты, а при втором и шестом прогонах она, наоборот, ушла налево. Может быть, это не случайно? Что все это означает? Ответ: само по себе – абсолютно ничего. Если бы мы создали модель и программу и ограничились получением нескольких графиков, как на рисунке 4.1, то мы бы зря потратили время. Ввиду вероятностного характера протекающих в модели процессов, смысл имеют не отдельные результаты прогонов программы, а усредненные характеристики по многим прогонам. В этом состоит суть так называемого метода Монте-Карло. Несмотря на то, что слово «метод» употреблено в единственном числе, на самом деле это целая категория совершенно разнообразных методов и подходов, которые можно охарактеризовать следующим образом. Если вы в процессе вычислений или моделирования хотя бы один раз использовали случайные числа не для вспомогательных целей, а по сути ваших расчетов, то можно считать, что вы использовали метод Монте-Карло. Ясно поэтому, что наша модель является типичной стохастической моделью в рамках подхода Монте-Карло. Поэтому необходимо прогонять ее не один и не шесть раз, как на рисунке 4.1, а много, очень много раз, чтобы «набрать статистику» и получить надежные (состоятельные, по терминологии математической статистики) средние значения интересующих нас величин.
В случае броуновского движения интерес обычно представляет, насколько далеко от первоначального положения отклонилась частица по прошествии определенного времени T, причем по абсолютной величине, направление значения не имеет. Мы должны, следовательно, прогнать программу, например, 10000 раз (количество прогонов обозначим MC) и по окончании каждого прогона запоминать конечную координату частицы X(T). Таким образом, получим массив длиной MC (обозначим его XMC). Разумеется, выполнять столько раз программу следует не вручную. Заключим основной цикл предыдущей программы в еще один внешний цикл длиной MC. Время наблюдения за системой T на этот раз сократим до 10. Новая программа имеет вид:
> restart:
> with(stats): randomize():
> T: =10:
> MC: =10000:
> M: =100: m: =1: u: =10: p: =0.75:
> c1: =evalf((M-m)/(M+m)): c2u: =evalf(u*2*m/(M+m)):
> X: =vector(T): V: =vector(T): XMC: =vector(MC):
> for i from 1 to MC do XMC[i]: =0: od:
> ra: =rand(1..100): roll_1: = rand(1..2):
> for ijk from 1 to MC do for k from 1 to T do V[k]: =0: X[k]: =0: od: for j from 1 to T-1 do X[j+1]: =evalf(X[j]+V[j]): q1: =ra()/100: q2: =roll_1(): if(q1< p) then if(q2=1) then V[j+1]: =V[j]*c1+c2u: else V[j+1]: =V[j]*c1-c2u: fi else V[j+1]: =V[j]: fi: od: XMC[ijk]: =X[T]: od:
Итак, элементы полученного массива XMC представляют собой координаты частицы в момент времени T, полученные при разных прогонах программы. Вычислим среднее значение элементов этого массива и их квадратов. Средние значения можно вычислить с помощью оператора describe[mean], входящего в библиотеку stats. Но, подобно оператору plot, требуется преобразовать XMC к формату простого (одинарного) списка:
> xx: = [ XMC[n] $n=1..MC]: xx2: = [ XMC[n]^2 $n=1..MC]:
> describe[mean](xx); describe[mean](xx2);
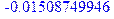
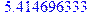 .
.
Как и следовало ожидать, среднее значение смещения близко к нулю, поскольку вероятность ударов молекул слева и справа одинакова. Что касается среднего квадрата смещения, то он, очевидно, зависит от параметров системы, и при увеличении числа прогонов программы, его величина будет стремиться к определенному значению (а среднее смещение все ближе будет приближаться к нулю). Читателю предлагается убедиться в этом, увеличивая число прогонов MC.
Наконец, настал момент, когда необходимо критически оценить сделанное и определить, в чем построенная модель плоха и как ее можно совершенствовать. Один момент очевиден: для сравнения с реальными системами размерность пространства, в которой движется частица, должна равняться трем. Кроме того, существенным недостатком модели является то, что в промежутках между столкновениями частица движется свободно (т.е. на нее не действуют никакие силы). В реальности частица подвержена вязкому трению со стороны среды [1]. Броуновская частица будет двигаться по зигзагообразному пути, удаляясь постепенно от начальной точки. Вычисления показывают, что значение среднего квадрата смещения броуновской частицы r 2 = x 2 + y 2 + z 2 описывается формулой:
< r 2 > = 6 kTBt, (4.5)
где B – подвижность частицы, которая обратно пропорциональна вязкости среды и размеру частицы. Эта формула, называемая формулой Эйнштейна, была со всей возможной тщательностью подтверждена экспериментально французским физиком Жаном Перреном (1870–1942). На основе измерения параметров движения броуновской частицы Перрен получил значения постоянной Больцмана и число Авогадро, хорошо согласующиеся в пределах ошибок измерений со значениями, полученными другими методами.
Итак, мы не можем сравнить нашу модель с экспериментом и с теорией, сопоставив полученное значение среднего квадрата смещения с формулой (4.4). Модель необходимо сделать ближе к реальности, что будет проведено в лабораторной работе. Здесь же отметим еще раз, что программа упрощенной модели составит основу для программы будущей модели. Тем не менее, для иллюстрирования методики сравнения результатов имитационного моделирования с теоретическими и/или экспериментальными данными, рассмотрим в следующем пункте упрощенный вариант блуждания по прямой, для которого имеется точное теоретическое описание.
4.2. Случайные блуждания на прямой: упрощенный случай
Рассмотрим стохастическое блуждание точки вдоль прямой «в чистом виде», т.е. вне всякой связи с динамикой. Допустим, что точка в каждый момент времени может с одинаковой вероятностью сместиться на одну единицу длины вправо или влево. Тогда имеется точный результат [2, с. 10–11]: вероятность того, что в момент времени T координата частицы будет равна k, дается следующим выражением:
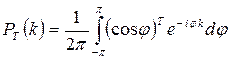 . (4.6)
. (4.6)
Для имитационного моделирования системы модифицируем программу п. 4.1. Ясно, что теперь программа будет существенно проще: не будет массива скорости, достаточно использовать только одно бинарное случайное число, расчет нового значения координаты будет выполняться по совсем простой формуле 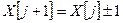 . Программа имеет вид:
. Программа имеет вид:
> restart:
> with(stats): randomize():
> T: =10:
> MC: =100000:
> X: =vector(T): XMC: =vector(MC):
> for i from 1 to MC do XMC[i]: =0: od:
> roll_1: = rand(1..2):
> for ijk from 1 to MC do for k from 1 to T do X[k]: =0: od: for j from 1 to T-1 do q2: =roll_1(): if(q2=1) then X[j+1]: =X[j]+1: else X[j+1]: =X[j]-1: fi: od: XMC[ijk]: =X[T]: od:
> xx: = [ XMC[n] $n=1..MC]: xx2: = [ XMC[n]^2 $n=1..MC]:
> evalf(describe[mean](xx)); evalf(describe[mean](xx2));
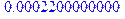
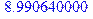 .
.
Первый результат понятен: ввиду равноправия левого и правого, среднее смещение равно нулю. Второе значение – средний квадрат смещения – явно равно 9. Вычисляя с большим количеством прогонов, т.е. увеличивая MC еще на порядок – до 106, получаем еще более точное значение
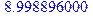 .
.
Соответствует ли полученное значение среднего квадрата смещения истинному распределению вероятностей (4.6)? Вычислим вероятности по формуле (4.6), имея в виду, что в вышеприведенной программе мы фактически рассматривали не T, а T-1 шагов блужданий:
> for j from -(T-1) to T-1 do w[j]: =evalf(int(cos(phi)^(T-1)*exp(-I*phi*j), phi=-Pi..Pi)/2/Pi); od:
Любое распределение вероятностей полного (т.е. всех возможных) набора событий должно быть нормировано на единицу, что необходимо всегда обязательно проверять, вычисляя сумму всех значений вероятностей:
> sum(w[jjk], jjk=-(T-1)..T-1);
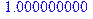 .
.
Итак, под именем w вычислено точное распределение вероятностей координат частицы после T-1 случайных шагов. Вычислим те же вероятности по результатам нашего имитационного моделирования. Для этого для каждого значения координаты, необходимо посчитать, сколько раз среди наших MC прогонов, после T-1 шагов, получалось это значение координаты, и разделить на MC:
> for y from –(T-1) to T-1 do S[y]: =0: for jj from 1 to MC do if(XMC[jj]=y) then S[y]: =S[y]+1: fi: od: P[y]: =evalf(S[y]/MC): od:
По терминологии математической статистики, P – это так называемые выборочные значения вероятностей (фактически выборочные частоты), т.е. полученные из выборки конечного объема, в данном случае MC. Сравним выборочные вероятности для объема MC=100000 и точные, распечатав их в формате list (простой список):
> [P[a] $a=0..T-1];
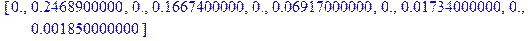
> [w[a] $a=0..T-1];
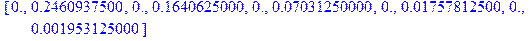
Видим, что имеется хорошее совпадение выборочного и точного распределений. По закону больших чисел, при увеличении объема выборки выборочные значения должны все более приближаться к истинным. Читателю предоставляется убедиться в этом, увеличив MC на порядок.
Наконец, вычислим средний квадрат координаты по точному распределению вероятностей w:
> sum(w[jjk]*jjk^2, jjk=-(T-1)..T-1);
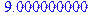 .
.
Оно действительно равно 9, как мы и получили в нашем имитационном эксперименте!