Введение. В отличие от стандартных задач диффузии и теплопроводности, относящихся к классической математической физике

В отличие от стандартных задач диффузии и теплопроводности, относящихся к классической математической физике, проблема модификации процессов переноса в движущихся средах является до сих пор нерешенной в полном объеме. Движение среды меняет не только эффективную скорость диффузии, но и характер зависимости диффузионного потока (характерного смещения) от времени. Более сильная (по сравнению с обычной для стандартной диффузии корневой) зависимость от времени называется супердиффузией, а более слабая – субдиффузией. Как правило, неоднородное движение среды приводит к супердиффузии, что необходимо иметь в виду при многочисленных практических приложениях этой задачи, например, для расчетов распространения выбросов ядовитых веществ в атмосфере или загрязнений в океане, миграции примесей в плазменном или химическом реакторе и многих других.

Возможно ли течение, реализующее режим субдиффузии в отсутствие специальных " ловушек" для диффундирующих частиц, пока неизвестно. Идея постановки данной работы состояла в том, что в условиях течения по несимметричной области, когда ширина узкого слоя оказывается порядка длины свободного пробега частицы, может быть реализован и режим субдиффузии. Так это или нет, предстоит выяснить в результате проведения предлагаемого численного эксперимента.

Рассмотрим модель пробных частиц (dye particles). Частицы в этой модели испытывают воздействие среды, но не изменяют ее параметров. В общем случае поток частиц имеет вид:

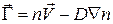(4.18)

где первое слагаемое представляет конвективный поток частиц плотности n в поле скоростей 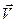, второе слагаемое соответствует диффузионному переносу с коэффициентом диффузии D:

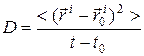, (4.19)

где радиус-вектор 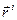(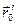) обозначает положение i-ой частицы в момент времени t (t₀), а угловые скобки означают усреднение по ансамблю пробных частиц:

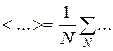, (4.20)

где N – полное количество пробных частиц.