Регулярное движение

Для расчета линий тока в асимметричном вихре необходимо рассчитать уравнение непрерывности. Непрерывность линий тока описывается уравнением

,

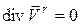которое сводится в двумерном случае к уравнению Лапласа для потенциала скорости φ (x, y,):

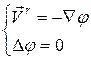, (4.21)

а компоненты скорости имеют вид:

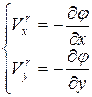(4.22)

Кроме того, необходимо задать ненулевой ротор

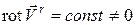, (4.23)

чтобы описать вихревое движение. Для того чтобы совместить уравнения (4.21) и (4.23), область вихря разбивается на две части и задача на регулярное движение решается в два этапа: для верхней половины вихря I и для нижней половины II (рисунок 4.10). По отдельности движение в этих областях будет потенциальным и описывается уравнением Лапласа (4.21) с заданными граничными условиями на границах разделения этих областей А и В на перепад функции φ (x, y,):

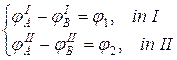(4.24)

Сшивка решений на границах А и В происходит с помощью подбора граничного условия (4.24) из условия непрерывности скорости (4.22). Граничные условия на функцию φ на остальных границах накладываются таким образом, что регулярное движение частиц (4.22) не выносит частицы из зоны вихря.