Оптимальный фильтр Винера

Подход к задаче оптимальной фильтрации может быть как статистическим, так и детерминированным. Сначала рассмотрим статис­тический вариант.

Пусть входной дискретный, случайный сигнал x(k) обрабатывается не рекурсивным дискретным фильтром порядка N, коэффици­енты которого могут быть представлены вектор-столбцом w = [ 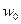, 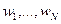]^т. Здесь символ T означает транспонирование вектора-строки в вектор-столбец. Теперь выход­ной сигнал фильтра можно записать

y(k) = u^T(k)w, (5.1)

где u(k) = [x(k), x(k - 1),..., x(k - N) ] 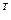– вектор-столбец содержимого линии задержки фильтра на k-м шаге.

Кроме того, имеется образцовый (также случайный) сигнал d(k). Ошибка воспроиз­ведения образцового сигнала равна

e(k) =d(k) –y(k)=d(k) - u^T(k)w (5.2)

Необходимо найти такие коэффициенты фильтра w, которые обеспечивают максимальную близость выходного сигнала фильтра к образцовому, т.е. минимизируют ошибку e(k). Поскольку e(k) также является случайным процессом, в качестве меры ее величины разумно принять средний квадрат. Таким образом, оптимизируемый функционал выглядит так:

(Здесь черта означает статистическое осреднение дискретной, случайной величины, т.е. вычисление математического ожидания или средневзвешенной суммы из N+1 слагаемых.) Квадрат ошибки равен

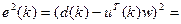
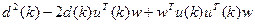
(конечно, здесь операции выполняются с помощью скалярного произведения векторов).

Статистически усредняя это выражение, получаем следующее:

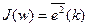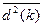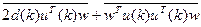= - (5.3)

Входящие в полученную формулу усред­ненные величины имеют следующий смысл:

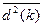= s²_d –средний квадрат об­разцового сигнала;

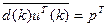– транспонированный вектор-столбец р взаимных корреляций между k- м отсчетом образцового сигнала и содержимого линии задержки фильтра. Если рассматриваемые случайные процессы x(k) и d(k) являются совместно стационарными, вектор взаимных корреляций не зависит от номера шага k;

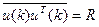– корреляционная матрица сигнала, имеющая размер (N +1) x (N + 1).

Для стационарного, случайного процесса корреляционная матрица име­ет вид матрицы Теплица, т.е. на ее диаго­налях стоят одинаковые величины:

R=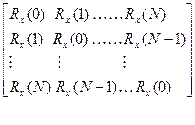

Здесь R_x(m) = 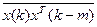– корреляционная функция (КФ) случайного процесса {x(k)}.