
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Детерминированная задача оптимизации
|
|
Рассматривая статистическую задачу оптимизации, мы считали входной сигнал случайным процессом и минимизировали средний квадрат ошибки воспроизведения образцового сигнала. Однако возможен и иной подход, не использующий статистические методы.
Пусть, как и раньше, обработке подвергается последовательность, состоящая из К отсчетов x(k), коэффициенты нерекурсивного фильтра образуют вектор-столбец w, a отсчеты образцового сигнала равны d(k). Выходной сигнал фильтра определяется формулой (5.1), а ошибка воспроизведения образцового сигнала – формулой (5.2).
Теперь оптимизационная задача формулируется так: необходимо найти такие коэффициенты фильтра w, чтобы норма ошибки воспроизведения образцового сигнала была минимальной:
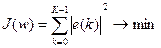 . (5.10)
. (5.10)
Для решения задачи в выражениях (5.1) и (5.2) перейдем к матричной записи, получая формулы для векторов-столбцов выходного сигнала у и для ошибки воспроизведения входного сигнала е:
y = UTw, e=d - UTw. (5.11)
Здесь d – вектор-столбец отсчетов образцового сигнала, a U – матрица, столбцы которой представляют собой содержимое линии задержки фильтра на разных тактах
U=[u(0), u(1), …, u(K-1)].
Выражение (5.10) для нормы ошибки можно переписать в матричном виде следующим образом:
J(w)=e 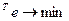 . (5.12)
. (5.12)
Подставляя (5.11) в (5.12), получаем
J(w) = (d - UTw)T (d - UT w) = dTd - wTUd - 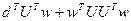 .
.
Для нахождения минимума необходимо вычислить градиент данного функционала и приравнять его нулю:
grad J(w) = -2Ud + 2UUT w = 0.
Отсюда легко получается искомое оптимальное решение:
w = (UU 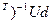 . (5.13)
. (5.13)
В формуле (5.13) прослеживается близкое родство с формулой (5.5), описывающей оптимальный в статистическом смысле фильтр Винера. Действительно, если учесть, что (UU 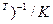 дает оценку корреляционной матрицы сигнала, полученную по одной реализации сигнала путем временного усреднения, a Ud / К является аналогичной оценкой взаимных корреляций между образцовым сигналом и содержимым линии задержки фильтра, то формулы (5.5) и (5.13) совпадут.
дает оценку корреляционной матрицы сигнала, полученную по одной реализации сигнала путем временного усреднения, a Ud / К является аналогичной оценкой взаимных корреляций между образцовым сигналом и содержимым линии задержки фильтра, то формулы (5.5) и (5.13) совпадут.