
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Расчет эквивалентной вероятности ошибочного приема двоичного элемента.
|
|
Наиболее распространенными помехоустойчивыми кодами являются блочные разделимые систематические коды. Кодовая комбинация такого кода имеет вид
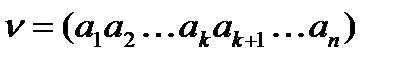 ,
,
в которой k элементов информационные, а 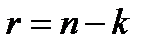 - контрольные проверочные элементы. Число проверочных элементов находится из условия
- контрольные проверочные элементы. Число проверочных элементов находится из условия
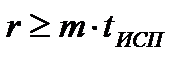 , (40)
, (40)
где 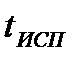 - кратность исправляемых ошибок; m – некоторый коэффициент, определяемый из условия
- кратность исправляемых ошибок; m – некоторый коэффициент, определяемый из условия
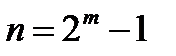 . (41)
. (41)
Для рассматриваемого примера варианта задания результаты расчета по формулам (40), (41) имеют вид:
 ,
,
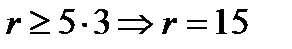 ,
,
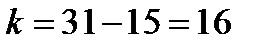 .
.
Значит, на каждые 16 информационных символов нужно добавить 15 контрольных проверочных символов, чтобы обеспечить требуемую исправляющую способность кода 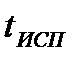 =3.
=3.
помехоустойчивого блочного кода вычисляется по формуле
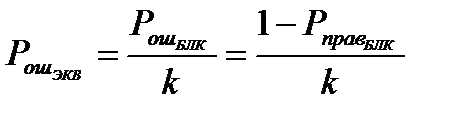 , (42)
, (42)
где  - вероятность ошибочного декодирования принятого блока;
- вероятность ошибочного декодирования принятого блока; 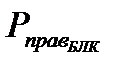 - вероятность правильного декодирования блока, которая может быть найдена как
- вероятность правильного декодирования блока, которая может быть найдена как
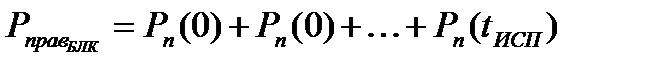 , (43)
, (43)
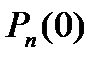 - вероятность того, что в блоке из
- вероятность того, что в блоке из  принятых символов содержится 0 ошибок;
принятых символов содержится 0 ошибок;
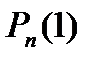 - вероятность того, что в блоке из
- вероятность того, что в блоке из  принятых символов содержится ровно одна ошибка;
принятых символов содержится ровно одна ошибка;
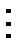
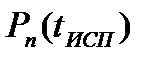 - вероятность того, что в блоке из
- вероятность того, что в блоке из  принятых символов содержится ровно
принятых символов содержится ровно 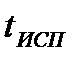 ошибок. Данные вероятности могут быть вычислены с помощью формулы Бернулли
ошибок. Данные вероятности могут быть вычислены с помощью формулы Бернулли
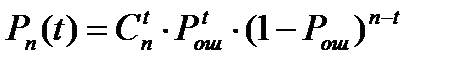 , (45)
, (45)
где 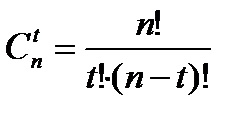 (46)
(46)
- число различных сочетаний из 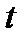 ошибок в блоке длиной
ошибок в блоке длиной  ;
; 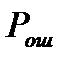 - вероятность ошибочного приёма одного двоичного символа в дискретном канале связи, найденная раннее в пункте 8.
- вероятность ошибочного приёма одного двоичного символа в дискретном канале связи, найденная раннее в пункте 8.
Для рассматриваемого примера варианта задания результаты расчета по формулам (45)-(46) имеют вид:
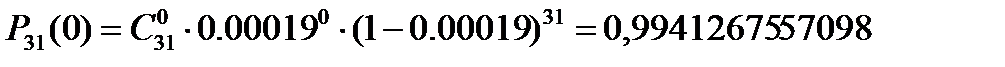 ,
,
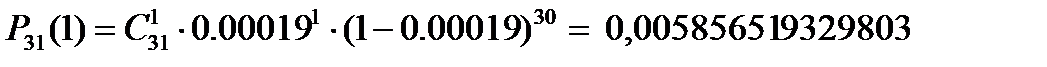 ,
,
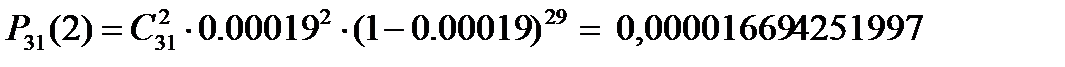 ,
,
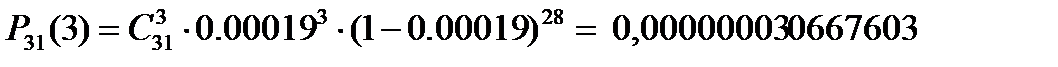 ,
,
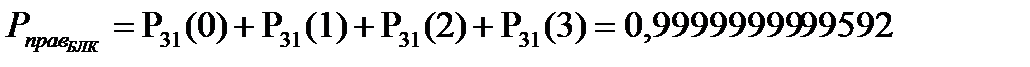
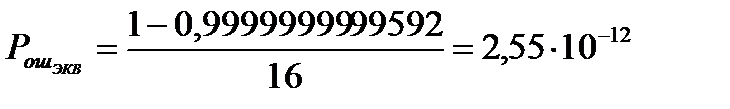 .
.
Можно сделать вывод, что при использовании помехоустойчивого кода вероятность ошибочного приёма намного уменьшилась.