
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пример выполнения индивидуального задания
|
|
Для малосигнального режима работы электронной схемы избирательного LC-усилителя (рис.6.29) сформировать математическую модель в базисе переменных состояния, используя алгоритм, основанный на уравнениях ветвей для координат (ВК-уравнениях). В качестве моделей активных многополюсных электронных компонентов использовать малосигнальные высокочастотные эквивалентные схемы, приведенные на рис. 6.30. Рассчитать и построить амплитудно-частотные, фазо-частотные и переходные характеристики, рассматривая в качестве переменных реакции схемы выходное напряжение, выходной и входной токи.
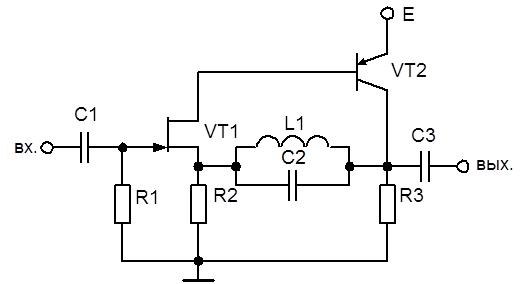
Рис. 6.29. Схема избирательного LC-усилителя

а) б)
Рис. 6.30. Эквивалентные схемы транзисторов: а – полевого с управляющим p-n-переходом; б - биполярного
Схема замещения усилителя по переменному току, сформированная с учетом всех реактивных компонентов, представлена на рис. 6.31.
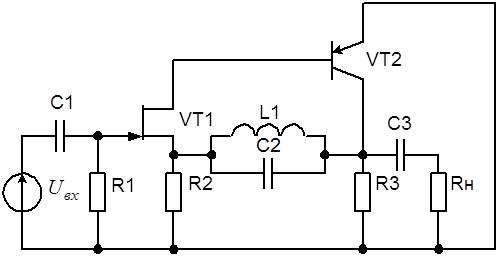
Рис. 6.31. Схема замещения избирательного LC-усилителя по переменному току
Замещая в схеме рис. активные многополюсные электронные компоненты заданными эквивалентными схемами, получаем схему замещения усилителя по переменному току, содержащую только двухполюсные компоненты, которая приведена на рис. 6.32.
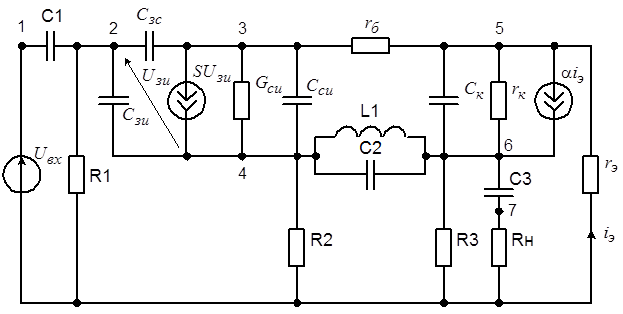
Рис. 6.32. Схема замещения избирательного LC-усилителя, содержащая двухполюсные компоненты
Полюсный граф, соответствующий схеме замещения рис.6.32, представлен на рис. 6.33.
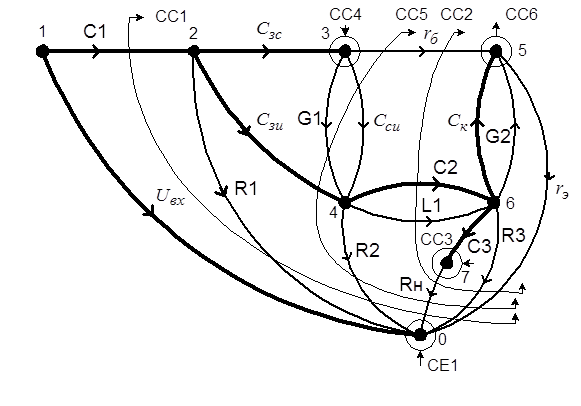
Рис. 6.33. Полюсный граф избирательного LC-усилителя
Для формирования математической модели в базисе переменных состояния на основе ВК-уравнений множество дуг полюсного графа следует разбить на 6 подмножеств:
– Е-дуги, отображающие ветви независимых источников ЭДС и короткозамкнутые дуги;
– С-дуги, отображающие емкостные ветви;
– G-дуги, соответствующие безреактивным y-ветвям;
– R-дуги, соответствующие безреактивным z-ветвям;
– L-дуги, отображающие индуктивные ветви;
– J-дуги, отображающие независимые источники тока и разомкнутые дуги.
При этом к y-дугам относятся C-дуги, G-дуги и J-дуги, а к z-дугам – Е-дуги, R-дуги и L-дуги.
С целью удобства формирования топологических матриц для обозначения дуг полюсного графа рис. 6.33 приняты обозначения соответствующих ветвей схемы замещения рис. 6.32. При этом параллельно включенные зависимый источник тока 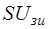 и ветвь с проводимостью
и ветвь с проводимостью 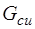 представлены эквивалентной дугой G1, а параллельно включенные зависимый источник тока
представлены эквивалентной дугой G1, а параллельно включенные зависимый источник тока 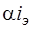 и ветвь с сопротивлением
и ветвь с сопротивлением 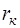 – эквивалентной дугой G2. Направления дуг G1 и G2 выбраны согласно направлениям соответствующих зависимых источников тока. Для представления матричного компонентного уравнения в упрощенной форме дуга, соответствующая управляющему по току
– эквивалентной дугой G2. Направления дуг G1 и G2 выбраны согласно направлениям соответствующих зависимых источников тока. Для представления матричного компонентного уравнения в упрощенной форме дуга, соответствующая управляющему по току 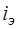 двухполюснику с сопротивлением
двухполюснику с сопротивлением 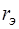 , отнесена к R-дугам. К R-дугам произвольно отнесены и все оставшиеся безреактивные ветви. Направление дуги
, отнесена к R-дугам. К R-дугам произвольно отнесены и все оставшиеся безреактивные ветви. Направление дуги 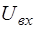 выбрано противоположно направлению задающей э.д.с., направление дуги
выбрано противоположно направлению задающей э.д.с., направление дуги 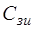 - противоположно направлению управляющего напряжения
- противоположно направлению управляющего напряжения  , направление дуги
, направление дуги 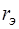 - согласно направлению управляющего тока
- согласно направлению управляющего тока 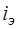 . Направления остальных дуг полюсного графа выбраны произвольно.
. Направления остальных дуг полюсного графа выбраны произвольно.
Полюсный граф избирательного усилителя (рис. 6.33) содержит 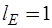 E-дуг (
E-дуг (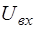 );
); 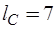 С-дуг (С1, С2, С3,
С-дуг (С1, С2, С3, 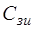 ,
, 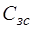 ,
, 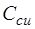 ,
, 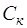 );
); 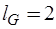 G-дуг (G1, G2);
G-дуг (G1, G2); 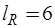 R-дуг (R1, R2, R3,
R-дуг (R1, R2, R3, 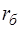 ,
, 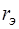 , Rн);
, Rн); 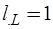 L-дуг (L1);
L-дуг (L1); 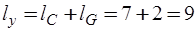 y-дуг;
y-дуг; 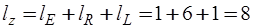 z-дуг;
z-дуг; 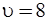 вершин;
вершин; 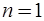 компоненту. В графе отсутствуют J-дуги, поэтому
компоненту. В графе отсутствуют J-дуги, поэтому 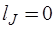 .
.
Для формирования модели в базисе переменных состояния на основе ВК-уравнений должно быть выбрано так называемое нормальное дерево, в которое сначала включают все Е-дуги, затем максимально возможное количество С-дуг, далее G-дуги, затем R-дуги и, наконец, минимально необходимое количество L-дуг. При этом все J-дуги остаются в дополнении нормального дерева. Если полюсный граф соответствует электронной схеме с правильной структурой, когда отсутствуют особые сечения и контуры, то все С-дуги войдут в состав нормального дерева, а все L-дуги – в состав его дополнения. Вектор переменных состояния будет содержать напряжения всех С-дуг нормального дерева и токи всех L-дуг дополнения. Таким образом, выбор нормального дерева обеспечивает исключение всех топологически зависимых переменных состояния.
В общем случае при выборе нормального дерева в соответствии с изложенными правилами топологические матрицы главных сечений и главных контуров могут быть представлены в виде:
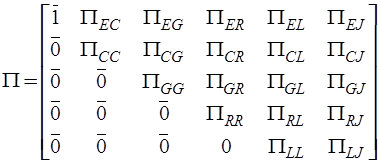 ,
,
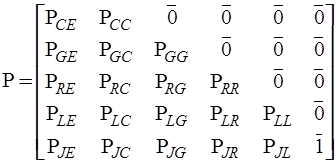 ,
,
где 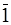 ,
, 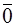 - единичные и нулевые подматрицы соответствующих размерностей. В обозначения остальных подматриц первый индекс указывает на тип дуг, определяющих соответствующие координаты (главные сечения для подматриц главных сечений или главные контуры для подматриц главных контуров), а второй индекс – тип дуг полюсного графа, которым соответствует подматрица.
- единичные и нулевые подматрицы соответствующих размерностей. В обозначения остальных подматриц первый индекс указывает на тип дуг, определяющих соответствующие координаты (главные сечения для подматриц главных сечений или главные контуры для подматриц главных контуров), а второй индекс – тип дуг полюсного графа, которым соответствует подматрица.
С учетом распределение дуг графа между y-дугами и z-дугами справедливо:
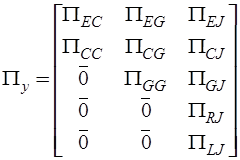 ,
,  ,
,
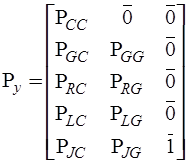 ,
, 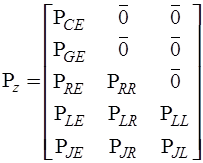 .
.
Если дуги в каждом подмножестве сгруппировать так, чтобы сначала следовали дуги нормального дерева, а затем хорды, топологические подматрицы можно представить в виде:
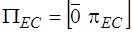 ,
, 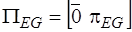 ,
, 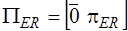 ,
, 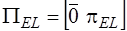 ,
, 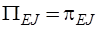 ;
;
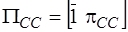 ,
,  ,
, 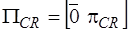 ,
, 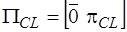 ,
, 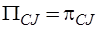 ;
;
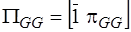 ,
, 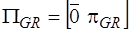 ,
, 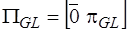 ,
, 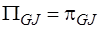 ;
;
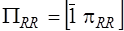 ,
, 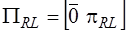 ,
, 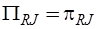 ;
;
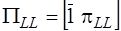 ,
, 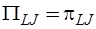 ;
;
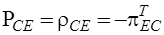 ,
, 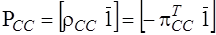 ;
;
 ,
,  ,
,
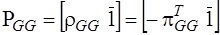 ;
;
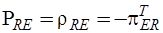 ,
, 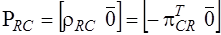 ,
,
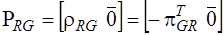 ,
,  ;
;
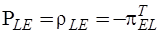 ,
, 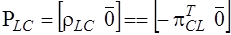 ,
,
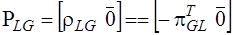 ,
, 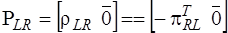 ,
,
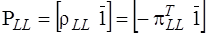 ;
;
 ,
,  ,
,
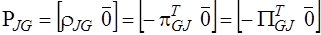 ,
,
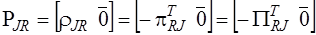 ,
,
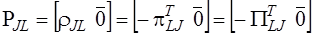 .
.
Нормальное дерево полюсного графа избирательного усилителя (рис. 6.33) должно содержать 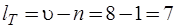 дуг. На рис. 6.33 дуги нормального дерева выделены жирными линиями. В состав нормального дерева включены
дуг. На рис. 6.33 дуги нормального дерева выделены жирными линиями. В состав нормального дерева включены 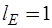 E-дуг (дуга
E-дуг (дуга 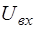 ) и
) и 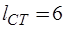 С-дуг (С1, С2, С3,
С-дуг (С1, С2, С3, 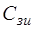 ,
, 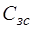 ,
, 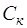 ). Нормальное дерево не содержит G-дуг (
). Нормальное дерево не содержит G-дуг ( ), R-дуг (
), R-дуг (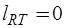 ) и L-дуг (
) и L-дуг (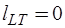 ). Дополнение нормального дерева включает
). Дополнение нормального дерева включает 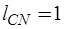 С-дугу (
С-дугу (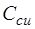 ), все G-дуги (
), все G-дуги (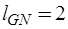 ), все R-дуги (
), все R-дуги (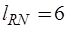 ) и L-дугу (
) и L-дугу (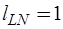 ). Таким образом, нормальное дерево полюсного графа рис. содержит
). Таким образом, нормальное дерево полюсного графа рис. содержит 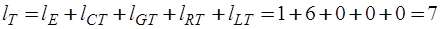 дуг, а дополнение нормального дерева –
дуг, а дополнение нормального дерева – 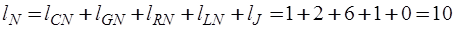 дуг.
дуг.
Рассматриваемая схема избирательного усилителя обладает неправильной структурой (является топологически вырожденной), так как содержит 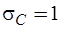 особый контур, образованный С-дугами
особый контур, образованный С-дугами 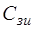 ,
, 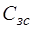 и
и 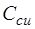 . Именно по этой причине в состав нормального дерева графа вошли не все С-дуги: произвольно выбранная одна из дуг особого контура (
. Именно по этой причине в состав нормального дерева графа вошли не все С-дуги: произвольно выбранная одна из дуг особого контура (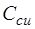 ) включена в состав дополнения дерева.
) включена в состав дополнения дерева.
Выбранное нормальное дерево определяет систему  главных сечений и
главных сечений и 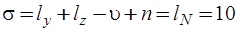 главных контуров. При этом
главных контуров. При этом 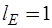 сечение (сечение СЕ1) определяется E-дугой дерева, а
сечение (сечение СЕ1) определяется E-дугой дерева, а 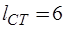 сечений (сечения СС1, СС2, СС3, СС4, СС5, СС6) – С-дугами дерева. Сечения, определяемые G-дугами, R-дугами и L-дугами в графе рис. отсутствуют. В системе главных контуров
сечений (сечения СС1, СС2, СС3, СС4, СС5, СС6) – С-дугами дерева. Сечения, определяемые G-дугами, R-дугами и L-дугами в графе рис. отсутствуют. В системе главных контуров 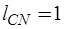 контур определяется С-дугой,
контур определяется С-дугой, 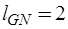 контура – G-дугами,
контура – G-дугами, 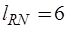 контуров – R-дугами,
контуров – R-дугами, 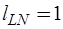 контур – L-дугой. Кроме того, в графе отсутствуют J-дуги. Следовательно, топологические матрицы главных сечений и главных контуров принимают вид:
контур – L-дугой. Кроме того, в графе отсутствуют J-дуги. Следовательно, топологические матрицы главных сечений и главных контуров принимают вид:
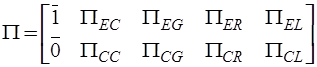 ,
,
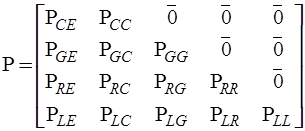 .
.
Так как топологические матрицы главных контуров могут быть получены из топологических матриц главных сечений, система главных контуров в графе рис. 6.33 не показана.
Подматрица  имеет размерность
имеет размерность 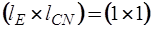 , а подматрица
, а подматрица  -
- 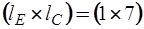 :
:
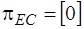 ,
, 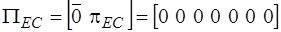 .
.
Подматрица 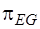 имеет размерность
имеет размерность  , а подматрица
, а подматрица 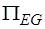 -
- 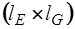 . Так как
. Так как 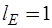 , а
, а 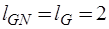 , то
, то
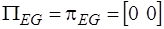 .
.
Подматрица 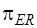 имеет размерность
имеет размерность 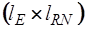 , а подматрица
, а подматрица 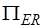 -
- 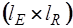 . Так как
. Так как 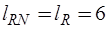 , то
, то
 .
.
Подматрица 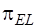 имеет размерность
имеет размерность 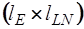 , а подматрица
, а подматрица 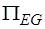 -
- 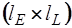 . Так как
. Так как 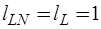 , то
, то
 .
.
Подматрица  имеет размерность
имеет размерность 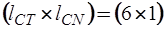 , а подматрица
, а подматрица  -
- 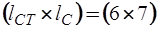 :
:
 ,
, 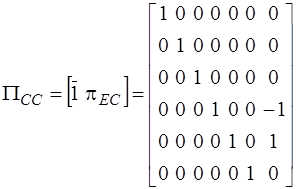 .
.
Подматрица 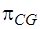 имеет размерность
имеет размерность 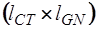 , а подматрица
, а подматрица 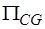 -
- 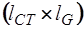 . Так как
. Так как 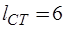 , а
, а 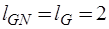 , то
, то
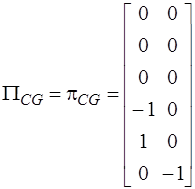 .
.
Подматрица 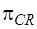 имеет размерность
имеет размерность 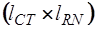 , а подматрица
, а подматрица 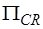 -
- 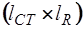 . Так как
. Так как 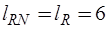 , то
, то
 .
.
Подматрица 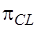 имеет размерность
имеет размерность 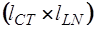 , а подматрица
, а подматрица 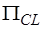 -
- 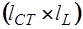 . Так как
. Так как 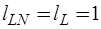 , то
, то
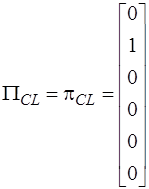 .
.
Используя связь топологических матриц главных контуров с топологическими матрицами главных сечений, найдем:
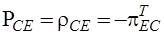 ,
,
 ,
,
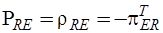 ,
,
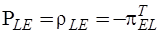 .
.
Подматрица 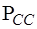 имеет размерность
имеет размерность 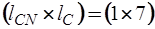 :
:
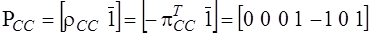 .
.
Подматрица  имеет размерность
имеет размерность 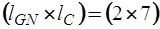 :
:
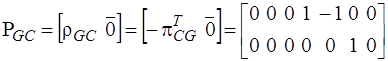 .
.
Подматрица 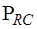 имеет размерность
имеет размерность 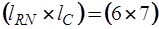 :
:
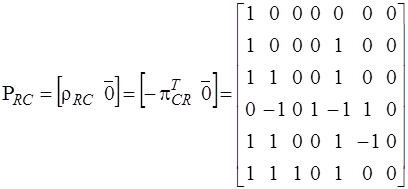 .
.
Подматрица 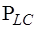 имеет размерность
имеет размерность 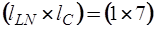 :
:
 .
.
Подматрица 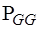 имеет размерность
имеет размерность 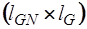 . Поскольку
. Поскольку 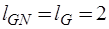 , то
, то
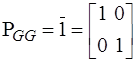 .
.
Подматрица 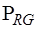 имеет размерность
имеет размерность 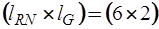 , а подматрица
, а подматрица 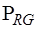 –
– 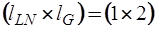 . Поскольку
. Поскольку 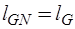 , то
, то
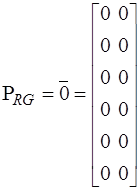 ,
, 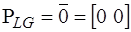 .
.
Подматрица  имеет размерность
имеет размерность 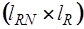 . Поскольку
. Поскольку 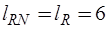 , то
, то
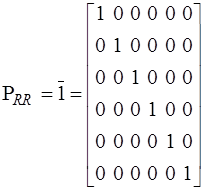 .
.
Подматрица 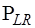 имеет размерность
имеет размерность 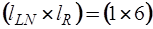 , Поскольку
, Поскольку  , то
, то
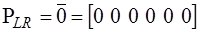 .
.
Подматрица 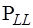 имеет размерность
имеет размерность 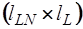 . Поскольку
. Поскольку 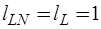 , то
, то
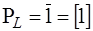 .
.
Группируя полученные топологические подматрицы в соответствии с распределением дуг полюсного графа на y-дуги и z-дуги, найдем
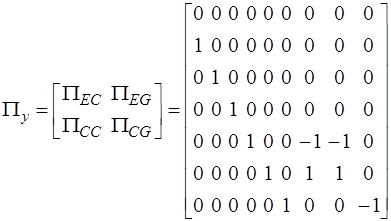 ,
,
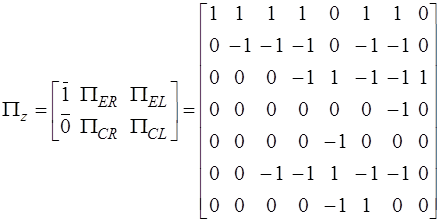 ,
,
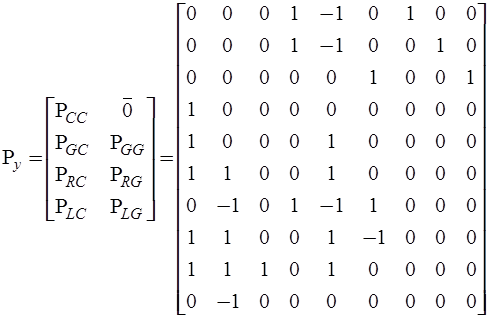 ,
,
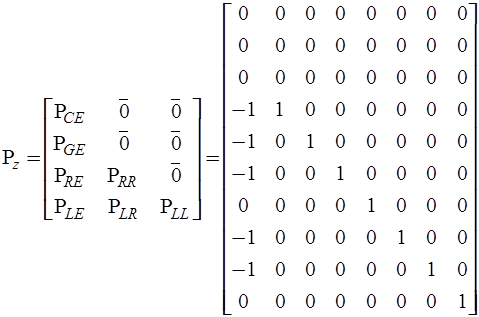 .
.
За счет отнесения всех С-дуг к у-дугам и всех L-дуг к z-дугам обобщенную компонентную матрицу можно представить в виде:
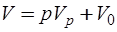 , (6.57)
, (6.57)
где 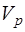 ,
, 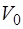 - компонентные матрицы параметров реактивных и безреактивных компонентов соответственно.
- компонентные матрицы параметров реактивных и безреактивных компонентов соответственно.
При записи топологических матриц в подмножестве y-дуг сначала следуют С-дуги, затем – G-дуги и в конце – J-дуги, а в подмножестве z-дуг – сначала E-дуги, затем – R-дуги и в конце – L-дуги, поэтому компонентные матрицы 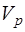 ,
, 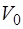 имеют вид:
имеют вид:
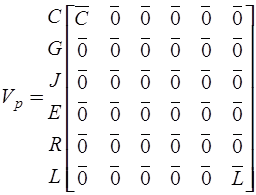 ,
,
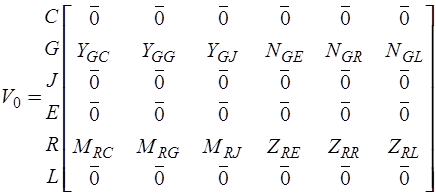 ,
,
где 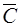 - диагональная матрица емкостей;
- диагональная матрица емкостей; 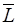 - матрица индуктивностей и взаимных индуктивностей (диагональная, если в схеме отсутствуют индуктивные связи);
- матрица индуктивностей и взаимных индуктивностей (диагональная, если в схеме отсутствуют индуктивные связи); 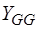 - матрица проводимостей G-дуг и управляющих проводимостей зависимых источников тока, управляемых напряжениями G-дуг;
- матрица проводимостей G-дуг и управляющих проводимостей зависимых источников тока, управляемых напряжениями G-дуг; 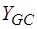 ,
,  - матрицы управляющих проводимостей зависимых источников тока, управляемых напряжениями С-дуг и J-дуг соответственно;
- матрицы управляющих проводимостей зависимых источников тока, управляемых напряжениями С-дуг и J-дуг соответственно; 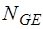 ,
, 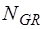 ,
, 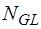 - матрицы управляющих проводимостей зависимых источников тока, управляемых токами E-дуг, R-дуг и J-дуг соответственно;
- матрицы управляющих проводимостей зависимых источников тока, управляемых токами E-дуг, R-дуг и J-дуг соответственно; 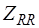 - матрица сопротивлений R-дуг и управляющих сопротивлений зависимых источников напряжения, управляемых токами R-дуг;
- матрица сопротивлений R-дуг и управляющих сопротивлений зависимых источников напряжения, управляемых токами R-дуг; 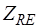 ,
, 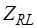 - матрицы управляющих сопротивлений зависимых источников напряжения, управляемых токами E-дуг и L-дуг соответственно;
- матрицы управляющих сопротивлений зависимых источников напряжения, управляемых токами E-дуг и L-дуг соответственно; 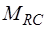 ,
, 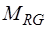 ,
,  - матрицы управляющих сопротивлений зависимых источников напряжения, управляемых напряжениями С-дуг, G-дуг и J-дуг соответственно.
- матрицы управляющих сопротивлений зависимых источников напряжения, управляемых напряжениями С-дуг, G-дуг и J-дуг соответственно.
Для рассматриваемой схемы избирательного усилителя матрица 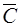 имеет
имеет 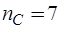 порядок:
порядок:
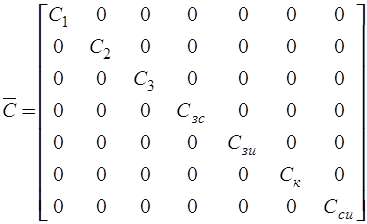 ,
,
а матрица 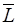 -
- 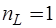 порядок:
порядок:
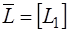 .
.
Полюсный граф рис. 6.33 не содержит J-дуг, поэтому компонентная матрица 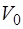 принимает вид:
принимает вид:
 .
.
Поскольку схема замещения рис. 6.32 не содержит зависимых источников напряжения, а также зависимых источников тока, управляемых токами G-дуг, E-дуг и L-дуг, то
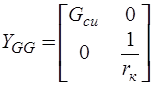 ,
,  ,
,
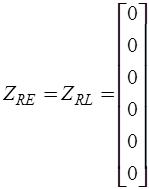 ,
, 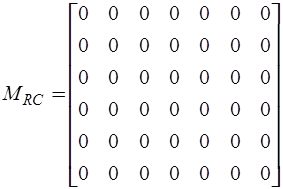 ,
,
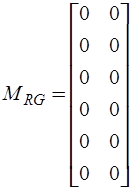 ,
, 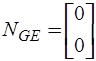 ,
, 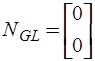 .
.
Зависимый источник тока, управляемый напряжением С-дуги (дуги 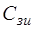 ) отображается в матрице
) отображается в матрице
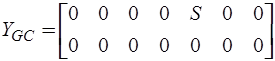 ,
,
а зависимый источник тока, управляемый током R-дуги (дуги 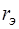 ) отображается в матрице
) отображается в матрице
 .
.
В результате компонентная матрица 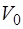 имеет вид
имеет вид
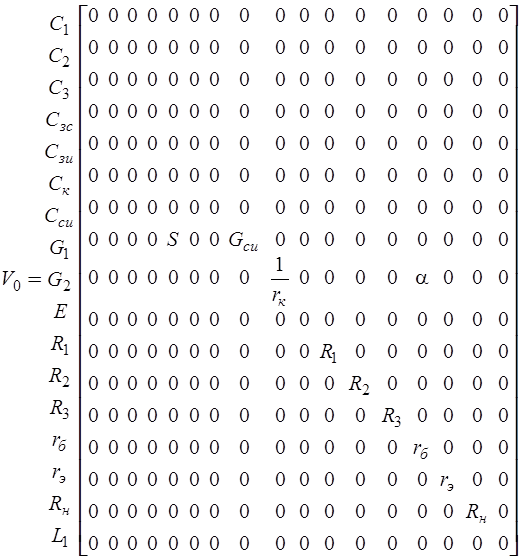 .
.
С учетом представления обобщенной компонентной матрицы 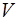 выражением (6.57) матрица эквивалентных параметров схемы, соответствующая системе уравнений ветвей для координат, принимает вид:
выражением (6.57) матрица эквивалентных параметров схемы, соответствующая системе уравнений ветвей для координат, принимает вид:
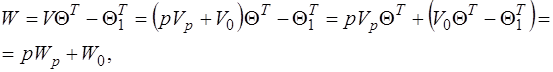
где  - матрица эквивалентных параметров реактивных компонентов схемы;
- матрица эквивалентных параметров реактивных компонентов схемы; 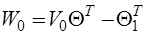 - матрица эквивалентных параметров безреактивных компонентов схемы;
- матрица эквивалентных параметров безреактивных компонентов схемы;  ,
, 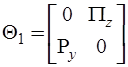 - обобщенные топологические матрицы.
- обобщенные топологические матрицы.
В результате система ВК-уравнений может быть преобразована:
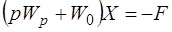 ,
,
откуда
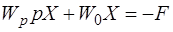 , (6.58)
, (6.58)
где 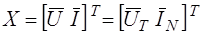 - вектор узловых напряжений, равных напряжениям ветвей нормального дерева (
- вектор узловых напряжений, равных напряжениям ветвей нормального дерева ( ) и контурных токов, равных токам хорд (
) и контурных токов, равных токам хорд (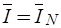 );
); 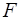 - вектор задающих токов и задающих э.д.с..
- вектор задающих токов и задающих э.д.с..
Принимая во внимание распределение дуг графа на подмножества и порядок записи топологических матриц, вектор 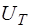 напряжений ветвей дерева, вектор
напряжений ветвей дерева, вектор 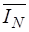 токов хорд и вектор
токов хорд и вектор 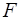 задающих токов и напряжений можно представить в виде:
задающих токов и напряжений можно представить в виде:
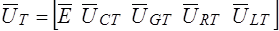 ,
,
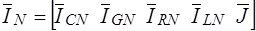 ,
,
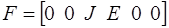 ,
,
тогда
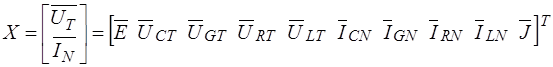
Из-за наличия нулевых строк и столбцов в компонентной матрице 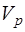 ранг матрицы
ранг матрицы 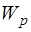 меньше ее порядка. После исключения нулевых столбцов из матрицы
меньше ее порядка. После исключения нулевых столбцов из матрицы 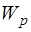 систему ВК-уравнений (6.58) можно записать
систему ВК-уравнений (6.58) можно записать
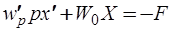 , (6.59)
, (6.59)
где  ,
,  .
.
С учетом принятого распределения дуг полюсного графа на подмножества матрица эквивалентных параметров 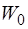 имеет вид:
имеет вид:
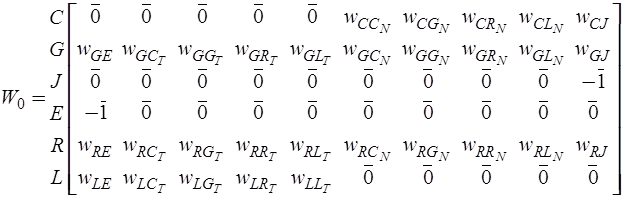
Из сопоставления матриц 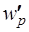 ,
, 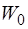 и векторов
и векторов 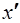 ,
, 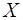 ,
, 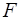 следует, что в системе ВК-уравнений (6.59) уравнения E-дуг и J-дуг представляют собой тождества, и, следовательно, могут быть исключены путем удаления из матриц соответствующих строк.
следует, что в системе ВК-уравнений (6.59) уравнения E-дуг и J-дуг представляют собой тождества, и, следовательно, могут быть исключены путем удаления из матриц соответствующих строк.
После удаления строк для разделения переменных состояния и алгебраических переменных из столбцов матриц 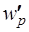 и
и 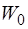 , соответствующих переменным состояния формируют матрицы
, соответствующих переменным состояния формируют матрицы
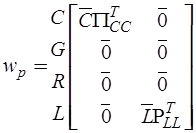 ,
, 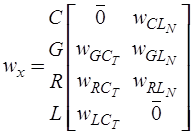 ,
,
из столбцов матрицы 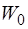 , соответствующих алгебраическим переменным, формируют матрицу
, соответствующих алгебраическим переменным, формируют матрицу
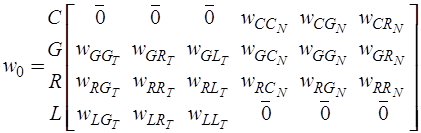 ,
,
из столбцов матриц 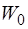 и
и 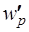 , соответствующих задающим токам и э.д.с. независимых источников, формируют матрицы
, соответствующих задающим токам и э.д.с. независимых источников, формируют матрицы
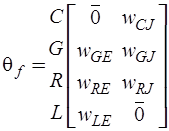 ,
, 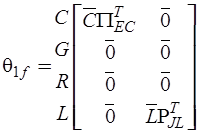 .
.
В результате система ВК-уравнений (6.59) принимает вид:
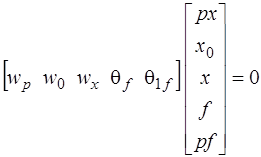
или
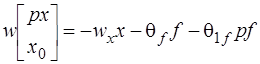 , (6.60)
, (6.60)
где 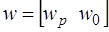 ;
; 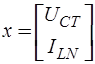 - вектор переменных состояния;
- вектор переменных состояния; 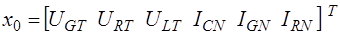 - вектор алгебраических переменных;
- вектор алгебраических переменных; 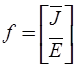 - вектор задающих токов и э.д.с. независимых источников.
- вектор задающих токов и э.д.с. независимых источников.
Если матрица 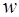 неособенная (
неособенная (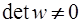 ), то из системы уравнений (6.60) следует:
), то из системы уравнений (6.60) следует:
 . (6.61)
. (6.61)
Выделяя в выражении (6.61) подматрицы, соответствующие переменным состояния и алгебраическим переменным, получаем уравнение
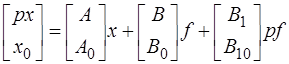 ,
,
которое разделяется на уравнение состояния в операторной форме

и алгебраическое уравнение
 .
.
Переходя от операторной формы записи уравнений к временной, получаем
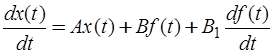 ,
,
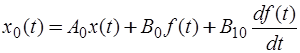 .
.
В системе ВК-уравнений рассматриваемой схемы избирательного усилителя вектор 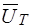 напряжений ветвей дерева содержит
напряжений ветвей дерева содержит 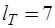 компонентов
компонентов
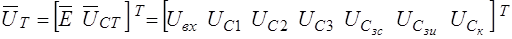 ,
,
вектор 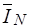 токов хорд –
токов хорд – 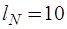 компонентов
компонентов
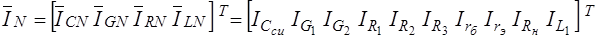 ,
,
а вектор 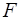 задающих токов и напряжений ветвей и вектор
задающих токов и напряжений ветвей и вектор 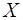 напряжений ветвей дерева и контурных токов –
напряжений ветвей дерева и контурных токов – 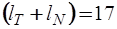 компонентов:
компонентов:
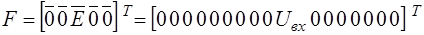 ,
,
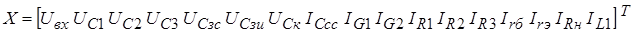
Матрицы 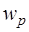 и
и 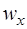 имеют размерность
имеют размерность 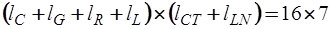
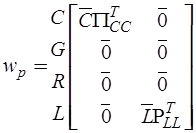 ,
, 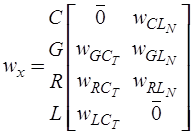 ,
,
матрица  -
- 
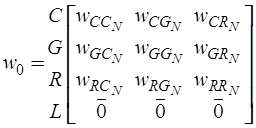 ,
,
матрицы 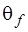 и
и  -
- 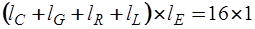
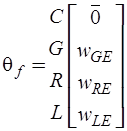 ,
, 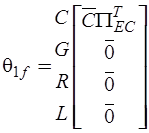 .
.
При этом поскольку 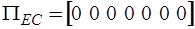 , то
, то 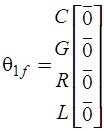 .
.
Используя матрицы 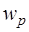 ,
, 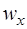 ,
,  ,
, 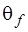 и
и 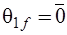 , получаем
, получаем
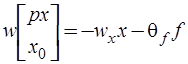 , (6.62)
, (6.62)
где 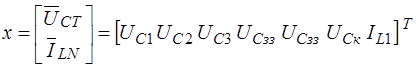 ,
, 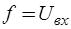 ,
,
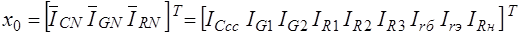 .
.
Поскольку 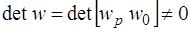 , то из (6.62) следует
, то из (6.62) следует
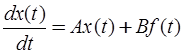 , (6.63)
, (6.63)
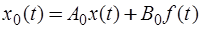 . (6.64)
. (6.64)
Матрица состояния 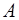 имеет
имеет 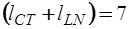 порядок и образована из первых
порядок и образована из первых 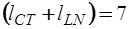 строк матрицы
строк матрицы  .
.
Матрица управления 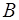 имеет размерность
имеет размерность  и образована из первых
и образована из первых 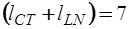 строк матрицы
строк матрицы 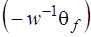 .
.
Матрица 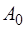 имеет размерность
имеет размерность 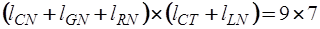 и образована из последних
и образована из последних  строк матрицы
строк матрицы  .
.
Матрица 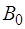 имеет размерность
имеет размерность 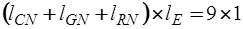 и образована из последних
и образована из последних  строк матрицы
строк матрицы 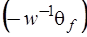 .
.
В качестве переменных реакции схемы заданы входной ток 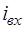 , выходной ток
, выходной ток 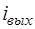 и выходное напряжение
и выходное напряжение 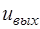 , поэтому вектор выходных переменных математической модели в базисе переменных состояния содержит
, поэтому вектор выходных переменных математической модели в базисе переменных состояния содержит 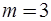 компонента:
компонента:
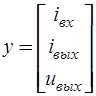 .
.
Из схемы замещения избирательного усилителя следует, что  . Учитывая положение переменной
. Учитывая положение переменной 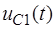 в векторе переменных состояния
в векторе переменных состояния 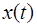 и используя уравнение состояния (6.63), находим:
и используя уравнение состояния (6.63), находим:
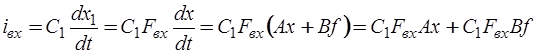 , (6.65)
, (6.65)
где 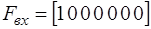 - вектор размерности
- вектор размерности 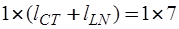 , выделяющий составляющую
, выделяющий составляющую 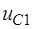 из вектора переменных состояния.
из вектора переменных состояния.
Для переменной 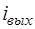 справедливо
справедливо 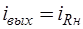 , поэтому, принимая во внимание положение
, поэтому, принимая во внимание положение 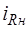 в векторе алгебраических переменных и применяя алгебраическое матричное уравнение (6.64), получим:
в векторе алгебраических переменных и применяя алгебраическое матричное уравнение (6.64), получим:
 , (6.66)
, (6.66)
где 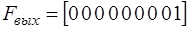 - вектор размерности
- вектор размерности 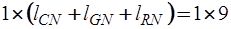 , выделяющий составляющую
, выделяющий составляющую 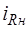 из вектора алгебраических переменных.
из вектора алгебраических переменных.
Поскольку 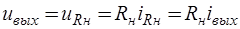 , то, используя (6.66), определяем:
, то, используя (6.66), определяем:
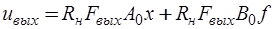 . (6.67)
. (6.67)
Записывая уравнения (6.65), (6.66) и (6.67) в матричной форме, получаем матричное выходное уравнение в базисе переменных состояния:
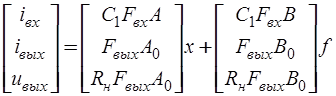
или
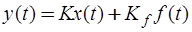 ,
,
где 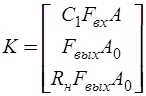 - матрица выхода;
- матрица выхода; 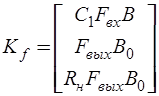 - матрица входа.
- матрица входа.
Матрица выхода 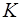 имеет размерность
имеет размерность 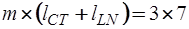 , а матрица входа
, а матрица входа 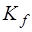 - размерность
- размерность 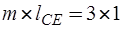 .
.
Таким образом, сформированная математическая модель схемы избирательного усилителя в базисе переменных состояний в обобщенной матричной форме имеет вид:
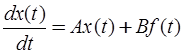 ,
,
(6.68)
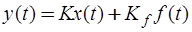 .
.
 Для получения комплексных частотных схемных функций, соответствующих заданным переменным реакции схемы представим систему уравнений (6.68) в операторной форме, применяя преобразование Фурье:
Для получения комплексных частотных схемных функций, соответствующих заданным переменным реакции схемы представим систему уравнений (6.68) в операторной форме, применяя преобразование Фурье:
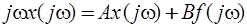 , (6.69)
, (6.69)
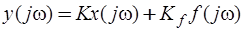 . (6.70)
. (6.70)
Определяя из уравнения (6.69) вектор 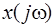 и подставляя его в уравнение (6.70), найдем
и подставляя его в уравнение (6.70), найдем
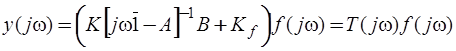 ,
,
где 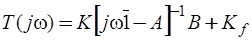 - матричная комплексная частотная функция.
- матричная комплексная частотная функция.
Матричная комплексная частотная функция в общем случае представляет собой комплексную матрицу, которая имеет размерность 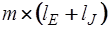 :
:
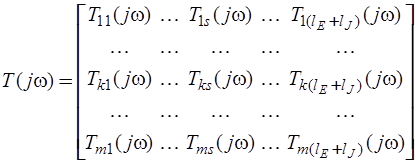 ,
,
где 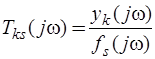 - комплексная частотная функция для переменной реакции
- комплексная частотная функция для переменной реакции  при переменной воздействия
при переменной воздействия 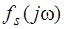 .
.
При использовании комплексных частотных функций расчет амплитудно-частотных и фазо-частотных характеристик осуществляется по выражениям
 ,
,
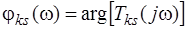 .
.
Для схемы избирательного усилителя рис. 6.29 матричная комплексная частотная функция имеет размерность 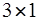 , причем:
, причем:
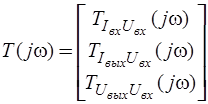 ,
,
где 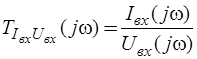 - комплексная частотная функция для переменной реакции
- комплексная частотная функция для переменной реакции 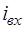 ;
; 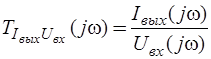 - комплексная частотная функция для переменной реакции
- комплексная частотная функция для переменной реакции 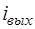 ;
; 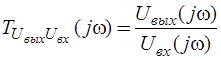 - комплексная частотная функция для переменной реакции
- комплексная частотная функция для переменной реакции 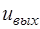 .
.
Аналитическое решение системы линейных неоднородных дифференциальных уравнений первого порядка (6.63) имеет вид:
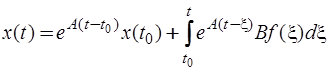 , (6.71)
, (6.71)
где 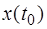 - вектор начальных условий переменных состояния в момент времени
- вектор начальных условий переменных состояния в момент времени 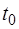 ;
; 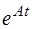 - экспоненциальная матрица (матричная экспонента).
- экспоненциальная матрица (матричная экспонента).
При 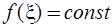 выражение (6.71) приводится к виду
выражение (6.71) приводится к виду
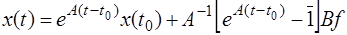 ,
,
а при нулевых начальных условиях (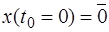 )
)
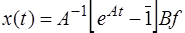 . (6.72)
. (6.72)
Подставляя (6.72) в выходное уравнение, получим
 , (6.73)
, (6.73)
где 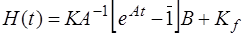 - матричная переходная функция.
- матричная переходная функция.
Матричная переходная функция в общем случае представляет собой матрицу, которая имеет размерность 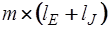 :
:
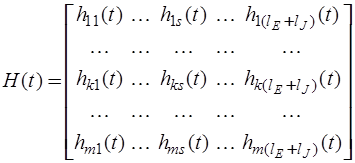 ,
,
где 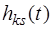 - переходная функция (характеристика) для переменной реакции
- переходная функция (характеристика) для переменной реакции 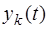 при переменной воздействия
при переменной воздействия 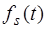 .
.
Матричная экспонента 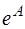 от квадратной матрицы
от квадратной матрицы 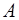 n-го порядка представляет собой квадратную матрицу n-го порядка, определяемую рядом Тейлора:
n-го порядка представляет собой квадратную матрицу n-го порядка, определяемую рядом Тейлора:
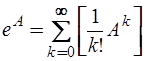 ,
,
где 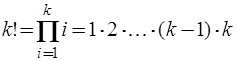 - факториал числа
- факториал числа 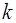 (по определению
(по определению 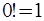 );
); 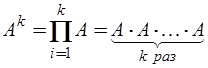 - k-ая степень матрицы
- k-ая степень матрицы 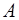 (по определению
(по определению 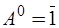 - единичная матрица n-го порядка).
- единичная матрица n-го порядка).
Для практических расчетов матричной экспоненты широко применяется формула Сильвестра, которая в случае простого спектра матрицы 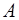 (отсутствия кратных собственных чисел) имеет вид:
(отсутствия кратных собственных чисел) имеет вид:
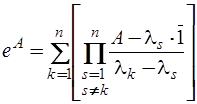 ,
,
где 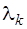 - собственные числа матрицы
- собственные числа матрицы 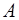 ;
; 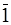 - единичная матрица n-го порядка.
- единичная матрица n-го порядка.
Наиболее простой вид матричная экспонента принимает для диагональной матрицы 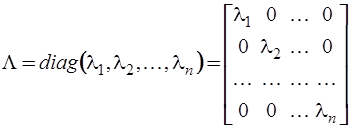 , когда
, когда
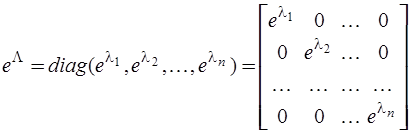 ,
,
то есть матричная экспонента является диагональной матрицей, по главной диагонали которой расположены экспоненциальные функции от элементов (собственных чисел) матрицы  .
.
Для упрощения расчета переходных характеристик матричную экспоненту в выражении (6.73) целесообразно привести к наиболее простому, то есть диагональному, виду. Если собственные числа матрицы состояния 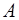 различны, то ее можно представить в виде
различны, то ее можно представить в виде
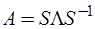 ,
,
где  - диагональная матрица собственных чисел матрицы
- диагональная матрица собственных чисел матрицы 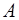 ;
; 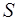 - неособенная матрица, столбцы которой представляют собой собственные векторы матрицы
- неособенная матрица, столбцы которой представляют собой собственные векторы матрицы 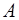 . Исходя из определения матричной экспоненты, можно доказать что
. Исходя из определения матричной экспоненты, можно доказать что
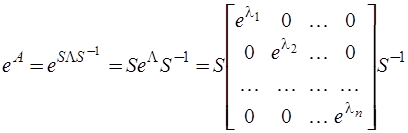 .
.
Тогда общее выражение для матричной переходной функции примет вид:
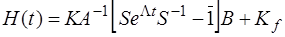 .
.
Для схемы избирательного усилителя рис. 6.29 матричная переходная функция имеет размерность 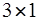 , причем:
, причем:
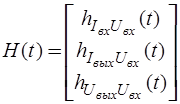 ,
,
где  - переходная функция для переменной реакции
- переходная функция для переменной реакции 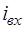 ;
; 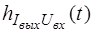 - переходная функция для переменной реакции
- переходная функция для переменной реакции 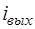 ;
; 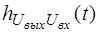 - переходная функция для переменной реакции
- переходная функция для переменной реакции 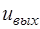 .
.
Формирование и реализация математической модели избирательного усилителя в базисе переменных состояния в вычислительной системе MathCad