Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Расчет средне квадратич отклонения по способу моментов
|
|
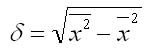
1. Коэффициентом осцилляции отражает относительную колеблемость крайних значений признака вокруг средней
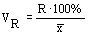 .
.
2. Относительное линейное отключение характеризует долю усредненного значения признака абсолютных отклонений от средней величины
 .
.
3. Коэффициент вариации позволяет судить об однородности совокупности:
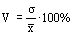
– < 17% – абсолютно однородная;
– 17–33%% – достаточно однородная;
– 35–40%% – недостаточно однородная;
– 40–60%% – это говорит о большой колеблемости совокупности.
| Виды дисперсии |
В зависимости от того, как представлена статистическая совокупность одним элементом или несколькими, различают следующие виды дисперсии:
– общая дисперсия;
– групповая дисперсия (внутригрупповая);
– средняя из групповых дисперсия;
– межгрупповая дисперсия.
Общая дисперсия оценивает колеблемость признака всех единиц совокупности без исключения:  . .
 – средняя в целом по совокупности;
f – частота в целом по совокупности.
Она отражает влияние всех причин и факторов, которые действуют на вариацию.
групповую дисперсию расчитывают Для характеристики вариации признаков внутри группы. Она рассчитывает колеблемость признака в каждой отдельной группе и представляет собой средний квадрат отклонений индивидуальных значений признаков от средней по каждой отдельно взятой группе: – средняя в целом по совокупности;
f – частота в целом по совокупности.
Она отражает влияние всех причин и факторов, которые действуют на вариацию.
групповую дисперсию расчитывают Для характеристики вариации признаков внутри группы. Она рассчитывает колеблемость признака в каждой отдельной группе и представляет собой средний квадрат отклонений индивидуальных значений признаков от средней по каждой отдельно взятой группе:  . .
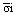 – показывает, что это групповая дисперсия.
Средняя из групповых дисперсия – это среднеарифметическая взвешенная из групповых дисперсий и определяется по формуле – показывает, что это групповая дисперсия.
Средняя из групповых дисперсия – это среднеарифметическая взвешенная из групповых дисперсий и определяется по формуле
 ,
где ,
где  – средняя из групповых дисперсия, fi – объем итоговой группы или число единиц в этой группе. Она характеризует случайную вариацию в каждой группе.
Межгрупповая дисперсия (дисперсия групповых средних) характеризует вариацию результативного признака под влиянием только одного фактора, положенного в равновесие группировки – средняя из групповых дисперсия, fi – объем итоговой группы или число единиц в этой группе. Она характеризует случайную вариацию в каждой группе.
Межгрупповая дисперсия (дисперсия групповых средних) характеризует вариацию результативного признака под влиянием только одного фактора, положенного в равновесие группировки 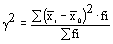 ,
где ,
где 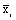 – групповые средние (средняя по отдельным группам), – групповые средние (средняя по отдельным группам), 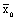 – общая средняя, fi – численность отдельной группы.
Правило сложения дисперсий для доли признака записывается так: – общая средняя, fi – численность отдельной группы.
Правило сложения дисперсий для доли признака записывается так:  – это правило сложения дисперсий имеет большое значение и позволяет выявить зависимость результатов от определенных факторов.
моменты распределения – это правило сложения дисперсий имеет большое значение и позволяет выявить зависимость результатов от определенных факторов.
моменты распределения 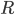 -го порядка -го порядка 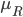 ,
Для несгруппированных данных: ,
Для несгруппированных данных:
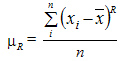 Для сгруппированных данных:
Для сгруппированных данных:
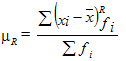 Момент первого порядка
Момент первого порядка 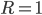 согласно свойству средней арифметической равен нулю согласно свойству средней арифметической равен нулю 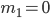 .
Момент второго порядка .
Момент второго порядка 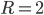 является дисперсией является дисперсией 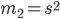 .
Моменты третьего .
Моменты третьего 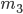 и четвертого и четвертого  порядков используются для построения показателей, оценивающих особенности формы эмпирических распределений.
С помощью момента третьего порядка измеряют степень скошенности или
ассиметричности распределения. порядков используются для построения показателей, оценивающих особенности формы эмпирических распределений.
С помощью момента третьего порядка измеряют степень скошенности или
ассиметричности распределения.
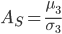
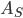 — коэффициент ассиметрии
9) ВЫБОРОЧНОЕ НАБЛЮДЕНИЕ — коэффициент ассиметрии
9) ВЫБОРОЧНОЕ НАБЛЮДЕНИЕ
|
Выборочное наблюдение применяется, когда применение сплошного наблюдения физически невозможно из-за большого массива данных или экономически нецелесообразно. Выборочное наблюдение есть такое несплошное наблюдение, при котором отбор подлежащих обследованию единиц осуществляется в случайном порядке, затем отобранная часть изучается, а далее результаты распространяются на всю исходную совокупность. В задачах по статистике наблюдение происходит таким образом, что эта часть отобранных единиц в уменьшенном масштабе представляет всю совокупность.
Генеральная совокупность — это совокупность, из которой производится отбор. Все обобщающие показатели данной совокупности называются генеральными.
Выборочная совокупность — это совокупность отобранных единиц. Все ее обобщающие показатели получили название выборочных.
Виды выборки по методу
Повторная выборка характеризуется тем, что численность единиц генеральной совокупности в процессе выборки остается постоянной.
Бесповторная выборка При такой выборке единица совокупности, попавшая в выборку, в генеральную совокупность не возвращают и в дальнейшем в выборке уже не участвует
Доля выборки рассчитывается как отношение числа единиц выборочной совокупности к числу единиц генеральной совокупности и определяется по формуле:

где N — объем генеральной совокупности (число входящих в нее единиц);
n — объем выборки (число обследованных единиц).
В статистике приняты следующие условные обозначения:
N - объем генеральной совокупности;
п - объем выборочной совокупности;
 - средняя в генеральной совокупности;
- средняя в генеральной совокупности;
 - средняя в выборочной совокупности;
- средняя в выборочной совокупности;
р - доля единиц в генеральной совокупности;
w - доля единиц в выборочной совокупности;
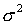 - генеральная дисперсия;
- генеральная дисперсия;
S2 - выборочная дисперсия;
 - среднее квадратическое отклонение признака в генеральной совокупности;
- среднее квадратическое отклонение признака в генеральной совокупности;
S - среднее квадратическое отклонение признака в выборочной совокупности.
| Повторный отбор | Бесповторный отбор |
| Ошибка выборочной средней | |
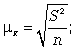
| 
|
| Ошибка выборочной доли | |
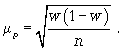
| 
|
| Предельная ошибка выборочной средней | |
| ∆ =µ*t | |
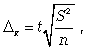
| 
|
| Предельная ошибка выборочной доли | |

| 
|
| Определение численности выборки | |

| 
|
Для типической выборки величина стандартной ошибки зависит от точности определения групповых средних.
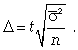
При серийной выборке величина ошибки выборки зависит не от числа исследуемых единиц, а от числа обследованных серий (s) и от величины межгрупповой дисперсии: