
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Изучение статистической связи
|
|
Статистика призвана изучать коммерческую деятельность с количественной стороны. Это осуществляется с помощью соответствующих приемов и методов статистики и математики.
Статистические показатели коммерческой деятельности могут состоять между собой в следующих основных видах связи: балансовой, компонентной, факторной и др.
^ Балансовая связь — характеризует зависимость между источниками формирования ресурсов (средств) и их использованием.
 , где
, где
 — остаток товаров на начало отчетного периода;
— остаток товаров на начало отчетного периода;
 — поступление товаров за период;
— поступление товаров за период;
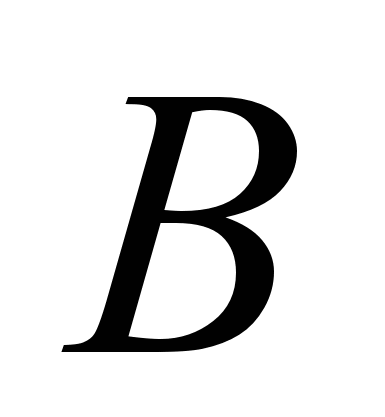 — выбытие товаров в изучаемом периоде;
— выбытие товаров в изучаемом периоде;
 — остаток товаров на конец отчетного периода.
— остаток товаров на конец отчетного периода.
Левая часть формулы характеризует предложение товаров
 , а правая часть — использование товарных ресурсов
, а правая часть — использование товарных ресурсов  .
.
^ Компонентные связи показателей коммерческой деятельности характеризуются тем, что изменение статистического показателя определяется изменением компонентов, входящих в этот показатель, как множители: 
В статистике коммерческой деятельности компонентные связи используются в индексном методе. Например, индекс товарооборота в фактических ценах 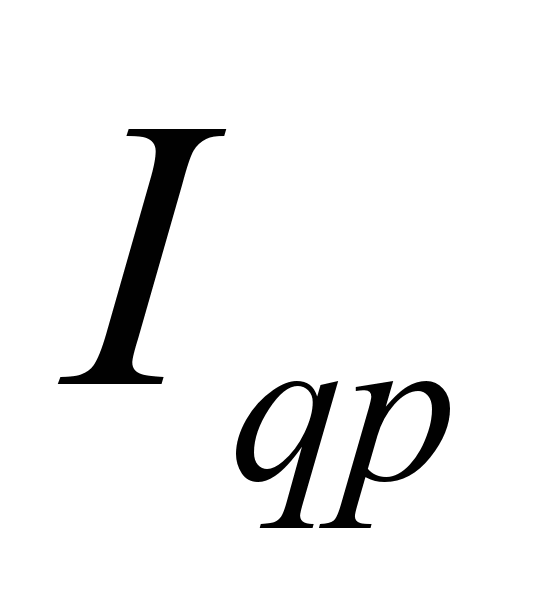 представляет произведение двух компонентов — индекса товарооборота в сопоставимых ценах
представляет произведение двух компонентов — индекса товарооборота в сопоставимых ценах  и индекса цен
и индекса цен 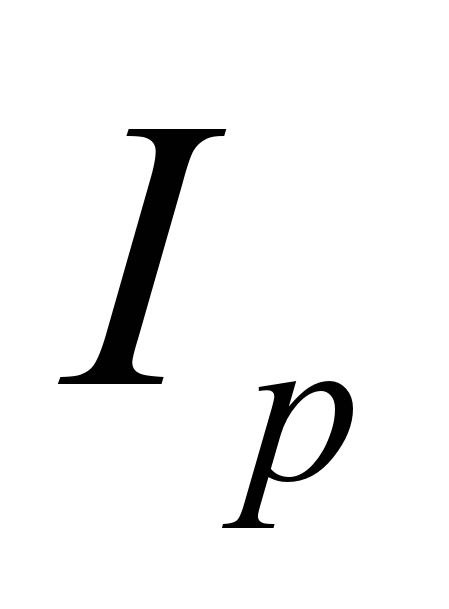 , т.е.
, т.е.  .
.
Важное значение компонентной связи состоит в том, что она позволяет определять величину одного из неизвестных компонентов:
 или
или 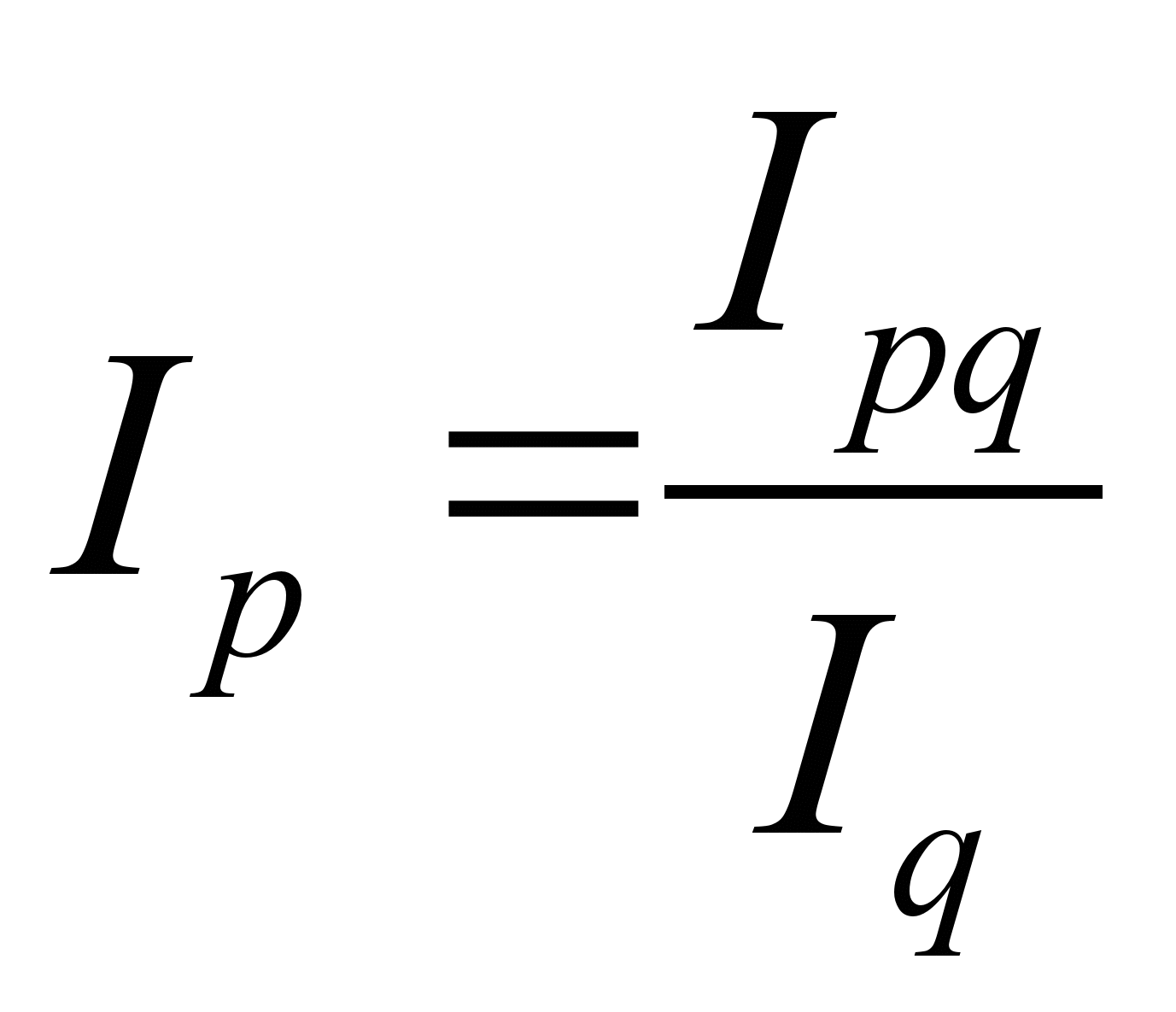
^ Факторные связи характеризуются тем, что они проявляются в согласованной вариации изучаемых показателей. При этом одни показатели выступают как факторные, а другие — как результативные.
Факторные связи могут рассматриваться как функциональные и корреляционные.
При функциональной связи изменение результативного признака  всецело зависит от изменения факторного признака
всецело зависит от изменения факторного признака  :
: 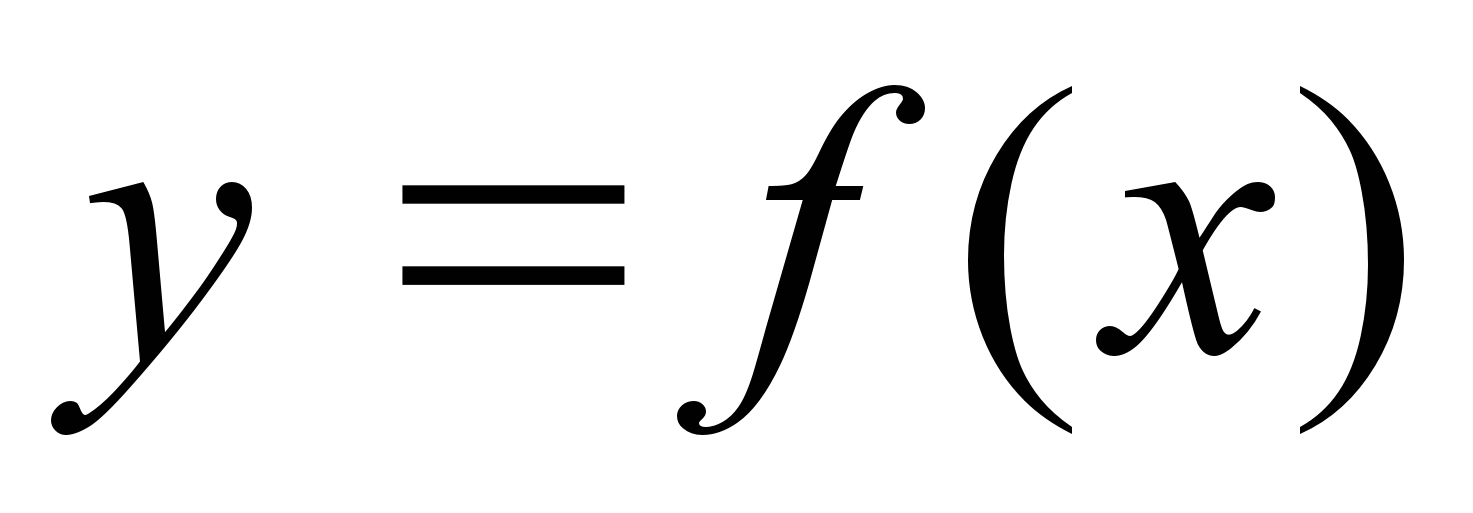
При корреляционной связи изменение результативного признака  не всецело зависит от факторного признака
не всецело зависит от факторного признака  , а лишь частично, так как возможно влияние прочих факторов £: Y= f(x) +£
, а лишь частично, так как возможно влияние прочих факторов £: Y= f(x) +£
коэффициент корреляции: 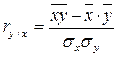 ,
,
где 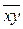 – средняя из произведений значений признаков ху;
– средняя из произведений значений признаков ху;  – средние значения признаков х и у;
– средние значения признаков х и у;  - средние квадратические отклонения признаков х и у. Он используется в том случае, если связь между признаками линейная
- средние квадратические отклонения признаков х и у. Он используется в том случае, если связь между признаками линейная
Построение таблиц – наиболее простой способ иллюстрации зависимости м/у показателями. Для анализа тесноты корреляционной зависимости использутся показтель корреляции рангов. Для этого от абсолютных показателей переходят к условным – рангам, принимая самое маленькое число.
Степень тесноты корреляционной связи количественно может быть оценена с помощью коэффициента корреляции, величина которого определяет характер связи
| Величина коэффициента корреляции | Характер связи |
| До ½ ± 0, 3½ | Практически отсутствует |
| ½ ± 0, 3½ - ½ ± 0, 5½ | Слабая |
| ½ ± 0, 5½ - ½ ± 0, 7½ | Умеренная |
| ½ ± 0, 7½ - ½ ± 1, 0½ | Сильная |
По направлению выделяют связь прямую и обратную.
При прямой связи с увеличением или уменьшением значений факторного признака происходит увеличение или уменьшение значений результативного. В случае обратной связи с увеличением значений факторного признака значения результативного убывают, и наоборот.
По аналитическому выражению выделяют связи: прямолинейные (или просто линейные) и нелинейные. Если статистическая связь между явлениями может быть приближенно выражена уравнением прямой линии, то ее называют линейной; если же она выражается уравнением какой-либо кривой линии то такую связь называют нелинейной или криволинейной.
1. Теснота связи между признаками определяется с помощью метода: