
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Аксиомы статики. Техническая механика
|
|
Техническая механика
Оглавление
| Введение | |
| 1. Теоретическая механика | |
| 1.1. Статика | |
| 1.1.1. Основные понятия и аксиомы статики | |
| 1.1.2. Сложение сил. система сходящихся сил | |
| 1.1.3. Системы параллельных сил, расположенных в одной плоскости | |
| 1.1.4. Система сил, произвольно расположенных в одной плоскости | |
| 1.1.5. Система пар и сил, произвольно расположенных в пространстве | |
| 1.2. Кинематика | |
| 1.2.1. Основные понятия | |
| 1.2.2. Кинематика точки | |
| 1.2.3. Кинематика твердого тела | |
| 1.3. Динамика | |
| 1.3.1. Основные законы и задачи динамики | |
| 1.3.2. Силы инерции | |
| 1.3.3. Работа и мощность | |
| 2. Теория механизмов и машин | |
| 2.1. Машины и их виды | |
| 2.2. Привода и машинные агрегаты | |
| 2.3. Механизмы и их виды | |
| 2.4. Типовые механизмы | |
| 2.5. Звенья механизмов | |
| 2.6. Кинематические пары | |
| 2.7. Кинематические цепи | |
| 2.8. Структура механизмов и ее дефекты | |
| 2.9. Рычажные механизмы | |
| 2.10. Структурный анализ рычажных механизмов | |
| 2.11. Состав структуры рычажных механизмов | |
| 2.12. Синтез рычажных механизмов | |
| 2.13. Кинематический анализ плоских механизмов | |
| 2.13.1. План положений механизма | |
| 2.13.2. План скоростей | |
| 2.13.3. План ускорений | |
| 2.13.4. Теорема подобия | |
| 2.14. Силовой анализ плоских механизмов | |
| 2.14.1. Классификация силовых факторов | |
| 2.14.2. Внешние силовые факторы | |
| 2.14.3. Внутренние силовые факторы | |
| 2.14.4. Теоретические силовые факторы | |
| 2.14.5. Теоретические силовые факторы для частных случаев движения | |
| 2.14.6. Кинетостатический анализ структурных групп 2-го класса | |
| 2.14.7. Кинетостатический анализ первичного механизма | |
| 2.14.8. Теорема И.Е. Жуковского | |
| 3. Сопротивление материалов | |
| 3.1. Реальный объект и расчетная схема | |
| 3.2. Внешние и внутренние силы. Метод сечений | |
| 3.3. Напряжения | |
| 3.4. Перемещения и деформации | |
| 3.5. Закон Гука и принцип независимости действия сил | |
| 3.6. Растяжение и сжатие | |
| 3.6.1. Внутренние силы и напряжения | |
| 3.6.2. Удлинение стержня и закон Гука | |
| 3.6.3. Потенциальная энергия деформации | |
| 3.6.4. Статически определимые и статически неопределимые системы | |
| 3.6.5. Напряженное и деформированное состояние при растяжении и сжатии | |
| 3.6.6. Основные механические характеристики материалов | |
| 3.7. Общие принципы расчета конструкции | |
| 3.8. Геометрические характеристики поперечных сечений бруса | |
| 3.8.1. Статические моменты сечения | |
| 3.8.2. Моменты инерции сечения | |
| 3.8.3. Главные оси и главные моменты инерции | |
| 3.9. Кручение | |
| 3.9.1. Кручение бруса с круглым поперечным сечением | |
| 3.9.2. Кручение бруса с некруглым поперечным сечением | |
| 3.9.3. Кручение тонкостенного бруса | |
| 3.10. Изгиб | |
| 3.10.1. Внутренние усилия в поперечных сечениях бруса | |
| 3.10.2. Основные дифференциальные соотношения теории изгиба | |
| 3.10.3. Напряжения при чистом изгибе | |
| 3.10.4. Касательные напряжения при поперечном изгибе | |
| 3.10.5. Перемещения при изгибе | |
| 3.11. Сложное сопротивление | |
| 3.11.1. Косой изгиб | |
| 3.11.2. Внецентренное растяжение и сжатие | |
| 3.12. Теории прочности | |
| 4. Основы проектирования деталей машин | |
| 4.1. Соединения деталей машин | |
| 4.1.1. Сварные соединения | |
| 4.1.2. Резьбовые соединения | |
| 4.1.3. Шпоночные соединения | |
| 4.1.4. Шлицевые соединения | |
| 4.2. Введение в теорию высшей пары | |
| 4.2.1. Теорема о высшей кинематической паре | |
| 4.2.2. Механизмы с высшими кинематическими парами | |
| 4.3. Зубчатые механизмы | |
| 4.3.1. Простые зубчатые механизмы | |
| 4.3.2. Пространственные механизмы с высшей кинематической парой | |
| 4.3.3. Плоские зубчатые механизмы | |
| 4.3.4. Эвольвента окружности и ее свойства | |
| 4.3.5. Эвольвентное зацепление и его свойства | |
| 4.3.6. Эвольвентные зубчатые колеса и их параметры | |
| 4.3.7. Методы получения формообразующей поверхности профилей зубьев | |
| 4.4. Исходный контур и исходный производящий контур | |
| 4.5. Виды зубчатых колес | |
| 4.6. Интерференция зубчатых колес | |
| 4.6.1. Влияние коэффициента смещения на параметры зубчатых колес | |
| 4.6.2. Блокирующий контур | |
| 4.6.3. Показатели качества зубчатых механизмов | |
| 4.7. Общие сведения о механических передачах | |
| 4.8. Зубчатые передачи | |
| 4.9. Цилиндрические прямозубые передачи внешнего зацепления | |
| 4.9.1. Материалы зубчатых колес | |
| 4.9.2. Силы в зацеплении прямозубых передач | |
| 4.9.3. Общие сведения о расчете на прочность цилиндрических эвольвентных зубчатых передач | |
| 4.9.4. Расчет на контактную прочность | |
| 4.9.5. Расчет на изгиб | |
| 4.10. Цилиндрические косозубые передачи | |
| 4.10.1. Эквивалентное колесо | |
| 4.10.2. Силы в зацеплении | |
| 4.10.3. Расчеты на прочность | |
| 4.11. Конические зубчатые передачи | |
| 4.11.1. Основные геометрические соотношения | |
| 4.11.2. Эквивалентное колесо | |
| 4.11.3. Силы в зацеплении | |
| 4.11.4. Расчет на контактную прочность | |
| 4.11.5. Расчет на изгиб | |
| 4.12. Червячные передачи | |
| 4.12.1. Классификация червячных передач | |
| 4.12.2. Основные геометрические соотношения в червячной передаче | |
| 4.12.3. Передаточное число | |
| 4.12.4. Силы в зацеплении | |
| 4.12.5. Материалы червячной пары | |
| 4.12.6. Расчет на прочность червячных передач | |
| 4.12.7. Тепловой расчет | |
| 4.13. Редукторы | |
| 4.13.1. Классификация редукторов | |
| 4.13.2. Зубчатые редукторы | |
| 4.14. Ременные передачи | |
| 4.14.1. Основные геометрические соотношения ременных передач | |
| 4.14.2. Силы в передаче | |
| 4.14.3. Скольжение ремня по шкивам. Передаточное число | |
| 4.14.4. Напряжения в ремне | |
| 4.14.5. Тяговая способность ременных передач | |
| 4.15. Цепные передачи | |
| 4.15.1. Приводные цепи | |
| 4.15.2. Звездочки | |
| 4.15.3. Передаточное число цепной передачи | |
| 4.15.4. Основные геометрические соотношения в цепных передачах | |
| 4.15.5. Силы в ветвях цепи | |
| 4.15.6. Расчет передачи роликовой (втулочной) цепью | |
| 4.15.7. Расчет передачи зубчатой цепью | |
| 4.16. Валы, оси, подшипники, муфты | |
| 4.16.1. Валы и оси | |
| 4.16.2. Подшипники качения | |
| 4.16.3. Муфты | |
| Библиографический список |
ВВЕДЕНИЕ
Дисциплина «Техническая механика» (ТМ) входит в цикл дисциплин, призванных обеспечить общетехническую подготовку инженеров немашиностроительных направлений и специальностей, владеющих основами проектирования, изготовления, эксплуатации и ремонта различных механических систем, изучение которых преследует следующие цели:
1) использование знаний, полученных студентами при изучении естественнонаучных и инженерных дисциплин;
2) предоставление знаний, необходимых для последующего освоения
специальных дисциплин и дисциплин специализаций, предусмотренных государственным образовательным стандартом (ГОС);
3) формирование у будущих специалистов знаний о строении механизмов, обучение методикам расчета на прочность, жесткость и устойчивость элементов конструкций;
4) овладение методами проектирования механизмов и устройств и навыками работы с машиностроительной, технической и технологической документацией;
5) получение навыков проведения проектировочных и проверочных
расчетов, а также навыков, необходимых для последующего изучения специальных дисциплин.
Дисциплина предусматривает формирование у будущих специалистов общетехнических, конструкторских навыков, а также навыков эксплуатации механических систем, применяемых в конкретных отраслях производства и транспорта в целом. В результате изучения дисциплины завершается и реализуется общетехническая подготовка студентов, создается база для усвоения дисциплин специализации.
Для приобретения умений и навыков, необходимых для профессиональной деятельности, изучение дисциплины «Техническая механика» преследует решение следующих задач:
1) обучение общим принципам проектирования и конструирования, построение моделей и алгоритмов расчетов изделий машиностроения по основным критериям работоспособности;
2) овладение методами теоретического анализа конструкций, механизмов, узлов и деталей машин электромеханического и энергетического оборудования, а также изучение основ конструирования и критериев работоспособности типовых деталей, узлов, механизмов и машин.
3) формирование навыков использования стандартов, технической справочной литературы и современной вычислительной техники, а также общенаучных (ОНК) и профессиональных (ПК) компетенций, которыми должен обладать инженер в современных условиях.
1. ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
Теоретическая механика – это наука о наиболее общих законах движения и равновесия материальных тел.
Движение, понимаемое в самом широком смысле этого слова, охватывает собой все происходящие в мире явления: перемещения тел в пространстве, тепловые и химические процессы, сознание и мышление.
Теоретическая механика изучает простейшую форму движения – механическое движение. «Кто не знаком с законами движения, тот не может познать природы» (Галилео Галилей).
Так как состояние равновесия есть частный случай механического движения, то в задачу теоретической механики входит также изучение равновесия материальных тел.
Основная цель механики – открытие, изучение и практическое применение общих законов движения и равновесия материальных тел.
Механика – одна из древнейших наук. Она возникла и развивалась под влиянием запросов общественной практики, а также благодаря любознательности человеческого разума. Рождение механики произошло одновременно с изобретением, изготовлением и применением человеком первых древнейших орудий труда – рычага, наклонной плоскости, блока, клина, винта, веревки.
Эти простейшие орудия сыграли роль научных методов, послуживших средством доказательства важнейших теорем и принципов механики. Архимедом (287–212 гг. до нашей эры) было обнаружено, что законы равновесия различных машин можно свести к равновесию рычага. Голландский ученый Стевин (1548–1620) с помощью наклонной плоскости открыл закон параллелограмма сил. Лагранж (1736–1833), используя систему блоков для доказательства основного принципа статики – принципа возможных перемещений. Равновесие веревки и веревочного многоугольника под действием сил послужило основой для создания графостатики, с помощью которой были выполнены многие расчеты стержневых систем. Таким образом, эти простейшие орудия, предназначенные для поднятия тяжестей, оказались средствами абстрактного научного мышления.
Теоретическая механика относится к числу физико-математических дисциплин. Законы механики носят физический характер.
Рабочими инструментами механики служат различные математические методы. Многие математики внесли существенный вклад в развитие механики.
Теоретическая механика является научной основой целого ряда инженерных дисциплин: сопротивления материалов, теории механизмов и машин, статики и динамики сооружений, строительной механики, деталей машин и других.
Теоретическая механика служит научной базой целого ряда важнейших направлений современной техники. Критерием достоверности результатов, к которым приходит любая наука, является практика. В этом отношении механика не представляет исключения. Производство, современная техника, астрономические наблюдения дают возможность убедиться в правильности ее выводов. Современная техника все чаще и чаще выдвигает перед наукой весьма сложные проблемы, разрешение которых возможно только на основании точного эксперимента и глубоких теоретических исследований.
Знание теоретической механики как научной базы современной техники совершенно необходимо каждому инженеру.
Теоретическая механика направляет творческую интуицию ученых и инженеров, давая им в краткой и ясной форме итог колоссального опыта человечества.
Развитие современной науки и техники указывает на все возрастающее значение теоретической механики.
Цель преподавания теоретической механики заключается в повышении уровня механико-математической подготовки студентов.
Задача изучения этой дисциплины – показать эффективность методов теоретической механики при решении сложных задач, поставленных наукой и техникой, овладеть понятиями, законами и принципами теоретической механики, навыками их применения в инженерной практике.
Теоретическую механику, как и математику, невозможно изучить без решения определенного числа задач.
Методами решения задач являются теоремы и принципы механики.
Теоретическая механика состоит из трех разделов – статики, кинематики и динамики.
Статика есть учение о силах. Статика рассматривает общие свойства сил и законы их сложения, а также условия равновесия различных систем сил.
Кинематика есть учение о движении материальных тел с геометрической стороны независимо от физических причин, вызывающих их движение.
Динамика есть учение о движении материальных тел под действием приложенных сил.
По своему построению теоретическая механика напоминает геометрию, потому что в ее основе лежат определения, аксиомы и теоремы.
1.1. Статика
Статикой называется раздел механики, в котором изучается общее учение о силах, а также условия равновесия материальных тел, находящихся под действием сил.
1.1.1. Основные понятия и аксиомы статики
Под равновесием понимается состояние покоя тела по отношению к другим материальным телам.
Абсолютно твердое тело – это тело, расстояние между любыми двумя точками которого всегда остается постоянным.
Чтобы твердое тело под действием некоторой системы сил находилось в равновесии (в покое), необходимо, чтобы эти силы удовлетворяли определенным условиям равновесия данной системы сил.
Основными задачами статики являются:
1. Сложение сил и приведение системы сил, действующих на твердое тело, к простейшему виду.
2. Определение условий равновесия систем сил, действующих на твердое тело.
Состояние равновесия или движение тела зависит от характера его механических взаимодействий с другими телами.
Сила – это величина количественной меры механического взаимодействия материальных тел.
Рассматриваемые в механике величины разделяют на векторные и скалярные.
Скалярные величины характеризуются только численными значениями.
Векторные величины характеризуются численными значениями и направлением в пространстве.
Сила является векторной величиной и ее действие на тело определяется численной величиной, или мерой силы, направлением силы, точкой приложением силы.
Сила (в механике) измеряется в Ньютонах (1 кг = 9, 81 ≈ 10 Н).
Основные определения
Прямая, вдоль которой направлена сила, называется линией действия силы.
Совокупность сил, действующих на какое-либо тело называется системой сил.
Тело, не связанное с другими телами, которому из данного положения можно сообщить любое перемещение в пространстве, называется свободным.
Если одну систему сил, действующую на тело, можно заменить другой системой, не изменяя при этом состояние данной системы, то такие две системы сил называются эквивалентными.
Система сил, под действием которой свободное твердое тело может находиться в покое, называется уравновешенной или эквивалентной нулю.
Равнодействующая сила – это сила, которая одна заменяет действие данной системы сил на твердое тело.
Сила, равная равнодействующей силе по модулю, но противоположно направленная по той же прямой, называется уравновешивающей.
Силы бывают внешними и внутренними:
Внешние силы действуют со стороны других материальных тел.
Внутренние – это силы, с которыми частицы данного тела действуют друг на друга.
Сила, приложенная к телу в какой-либо точке, называется сосредоточенной.
Силы, действующие на все точки данного объема или данной части поверхности тела, называются распределенными.
Аксиомы статики
Все теоремы и уравнения статики выводятся из нескольких исходных положений, принимаемых без математических доказательств. Эти положение называются аксиомами статики.
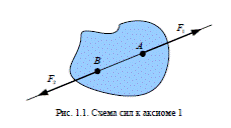
А к с и о м а 1. Если на свободное, абсолютно твердое тело действуют две силы, то твердое тело может находиться в равновесии тогда и только тогда, когда эти силы будут равны по модулю (F1 = F2) и направлены вдоль одной прямой в противоположные стороны (рис. 1.1). Следовательно, тело, на которое действует только одна сила, находиться в равновесии не может.
А к с и о м а 2. Действие данной системы сил на абсолютно твердое тело не изменится, если к ней прибавить или отнять уравновешивающую систему сил.
Следствие из 1-й и 2-й аксиом таково: действие силы на абсолютно твердое тело не изменится, если перенести точку приложения силы вдоль ее линии действия в любую другую точку тела.
Этим принципом можно пользоваться тогда, когда определяются условия равновесия той или иной конструкции и не рассматриваются возникающие в ее частях внутренние усилия. Следовательно, при определении внутренних усилий переносить точку приложения силы вдоль линии действия нельзя.
А к с и о м а 3. Две силы, приложенные к телу в одной точке, имеют равнодействующую, изображаемую диагональю параллелограмма, построенную на этих силах как на сторонах (рис. 1.2).
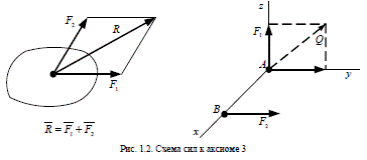
А к с и о м а 4. При всяком действии силы материального тела на другое имеет место такое же по величине, противоположное по направлению противодействие (рис. 1.3).

А к с и о м а 5. Равновесие деформируемого тела, находящегося под действием данной системы сил, не нарушится, если тело считать абсолютно твердым.