
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Плоской системы сил. Случай параллельных сил
|
|
Для равновесия любой плоской системы сил необходимо и достаточно, чтобы одновременно выполнялись условия
R = 0, M 0 = 0. (1.8)
Из этих равенств вытекают следующие три формы условий равновесия для произвольной плоской системы сил.
Первая форма условий равновесия заключается в том, что
Σ Fx = 0, Σ Fy = 0, Σ M 0 (Fn) = 0. (1.9)
т.е. для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы проекций всех сил на каждую из двух координат осей и сумма их моментов относительно любого центра, лежащего в плоскости действия были равны нулю.
Вторая форма условий равновесия выглядит так:
Σ mA (Fn) = 0, Σ mB (Fn) = 0, Σ Fx = 0, (1.10)
т.е. для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы моментов всех этих сил относительно каких-либо двух центров А и В и сумма их проекций на ось Ох, не перпендикулярную к прямой АВ, были равны нулю.
Третья форма условий равновесия выражается так:
Σ mA (Fn) = 0, Σ mB (Fn) = 0, Σ mC (Fn) = 0, (1.11)
т.е. для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы моментов всех этих сил относительно любых трех центров А, В, С, не лежащих на одной прямой, были равны нулю.
Для равновесия плоской системы параллельных сил необходимо и достаточно выполнение следующих условий:
Σ Fny = 0, Σ mO (Fn) = 0,
Σ mA (Fn) = 0, Σ mB (Fn) = 0.
При этом точки А и В не должны лежать на прямой, параллельной силам.
Решение задач. Приступая к решению задач, прежде всего, надо:
1) установить, равновесие какого именно тела следует рассмотреть в данной задаче;
2) выделить это тело и, рассматривая его как свободное, приложить к нему все действующие на тело силы и реакции отброшенных связей;
3) составить условия равновесия, применяя ту из форм этих условий, которая приводит к более простому решению.
Для получения более простых уравнений следует:
1) составляя уравнения проекций, проводить координатную ось перпендикулярно какой-нибудь неизвестной силе;
2) составляя уравнения моментов, брать центр моментов в точке, где пересекается больше неизвестных сил.
Решение многих задач статики сводится к определению реакций опор, с помощью которых закрепляются балки, рамы, мостовые фермы и т.д.
В технике чаще всего встречаются следующие три типа опорных закреплений.
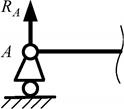
1. Шарнирно-подвижная опора (рис. 1.24).
Эта опора дает только одну опорную реакцию – RА, которая направлена по общей нормали к поверхности опирания.
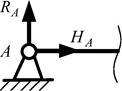
2. Шарнирно-неподвижная опора (рис. 1.25). Реакция NA такой опоры направлена произвольно в плоскости. Для удобства решения задач ее раскладывают на две составляющие – RA и HA:
|
|
|
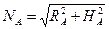
| Рис. 1.24. Шарнирноподвижная опора |
| Рис. 1.25. Шарнирнонеподвижная опора |
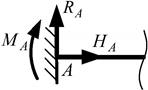
| Рис. 1.26. Жесткая заделка |
2. Жесткая заделка (рис 1.26). Возникает реакция NA, направленная произвольно в плоскости и момент MA. Реакцию NA раскладывают на две составляющие – RA и HA.