Центры тяжести геометрических фигур

Таблица 5.1

Вид фигуры	Рисунок	Площадь	Координата центра тяжести
Квадрат		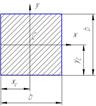A = b 2	y c = b /2
Продолжение таблицы 6.1.
Прямоугольник		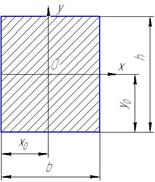A = b h	y c = h /2
Параллелограмм		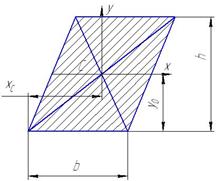A = b h	y c = h /2
Треугольник		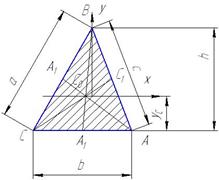A = b h /2	yc = h /3
Трапеция		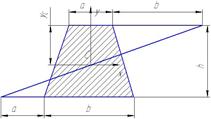A=(a+b) h/2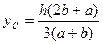
Шестигранник правильный		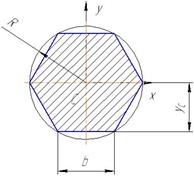A =2.598 R 2	yc =0.866 R
Продолжение таблицы 6.1.
Круг		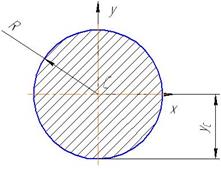A =π R 2	yc = R
Кольцо		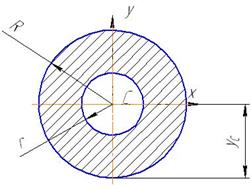A =π (R 2 – r 2 )	yc = R
Сегмент		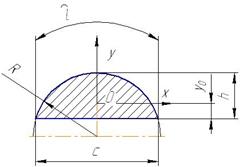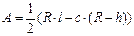Где
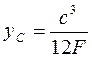
Сектор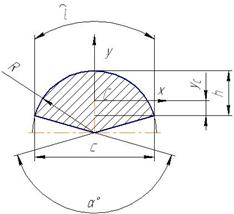
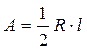
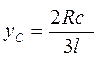
Полукруг		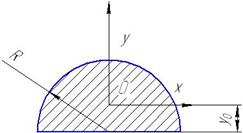A =π R 2 /2

Рассмотрим решение задачи на определение центра тяжести плоской фигуры.

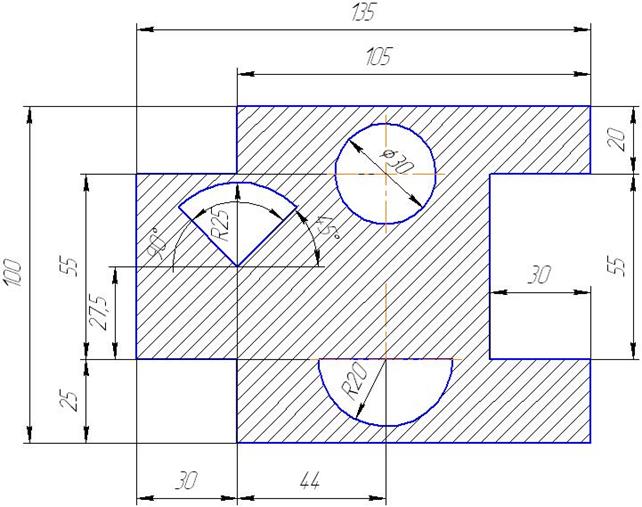
Рис. 6.2

На рис. 6.2 изображено сечение, состоящее из геометрических фигур. Определить центр тяжести этого сечения.

Решение

Разобьем сечение на геометрические фигуры (рис. 6.3):

прямоугольник 1 с размерами b = 105 мм, h = 100 мм,

прямоугольник 2 с размерами b = 30 мм, h = 55 мм,

прямоугольник 3 (выемка) с размерами b = 30 мм, h = 55 мм,

отверстие круглое 4 диаметром 30 мм, R = 15мм

отверстие полукруглое 5 радиусом R = 20мм

отверстие 6 сектор с углом 90° радиусом R = 25 мм.

Сечение, разбитое на стандартные фигуры, представлено на рис.6.3.

Принимаем оси координат, проходящие через левый нижний угол прямоугольника 1, и определяем площади фигур и координаты центра тяжести каждой фигуры.

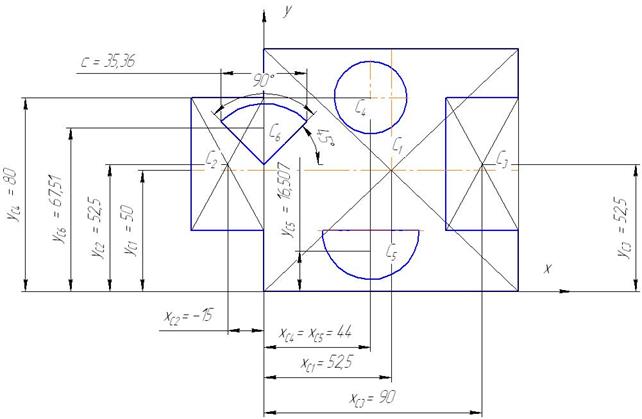
Рис. 6.3

Прямоугольник 1:

y_{c 1} = 50 мм, x_{c 1} = 52, 5 мм, A ₁ = 100 105 = 10500 мм².

Прямоугольник 2:

y_{c 2} = 52, 5 мм, x_{c 2} = -15 мм, A ₂ = 30 55 = 1650 мм².

Прямоугольник 3:

y_{c 3} = 52, 5 мм, x_{c 3} = 90 мм, A ₃ = 30 55 = 1650 мм²_.

Отверстие 4:

y_{c 4} = 80 мм, x_{c 4} = 44 мм, A ₄ = π 15² = 706, 5 мм²

Отверстие 5:

, x_{c 5} = 44 мм, A ₅= π R ²/2 =

= π 20²/2 = 628 мм².

Отверстие 6:

Длина дуги l = π R /2=3, 14 25/2 = 39, 25 мм

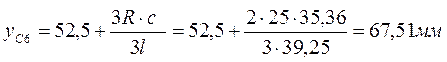, x_{c 5} = 44 мм,

A ₅= R l /2 = 25 39.25/2 = 490.65 мм².

Выполним расчет координат центра тяжести сечения по формулам:

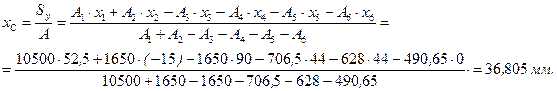
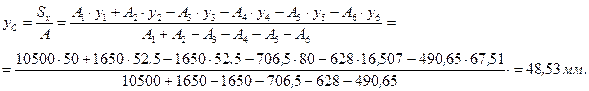
Найденный центр тяжести сечения изображен на рисунке 6.4.

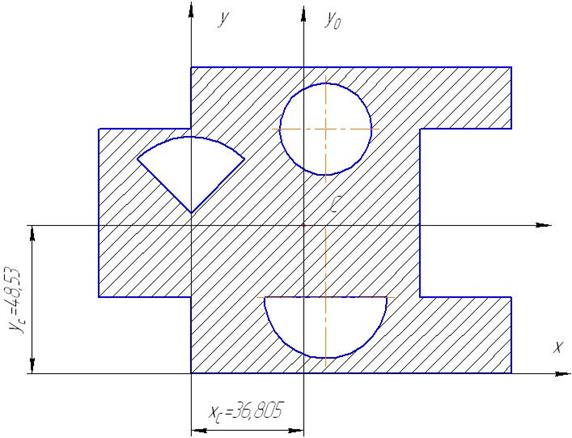
Рис. 6.4

Задания для самостоятельной работы приведены на рисунках 6.5 – 6.9.

Числовые значения переменных в табл.6.2.

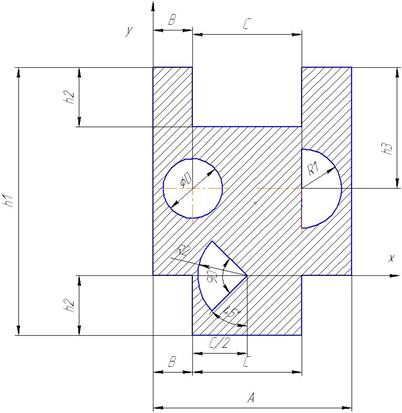
Рис. 6.5

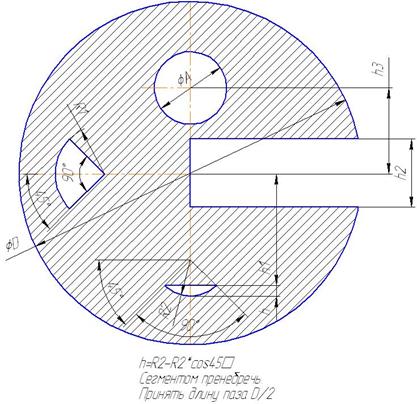
Рис. 6.6

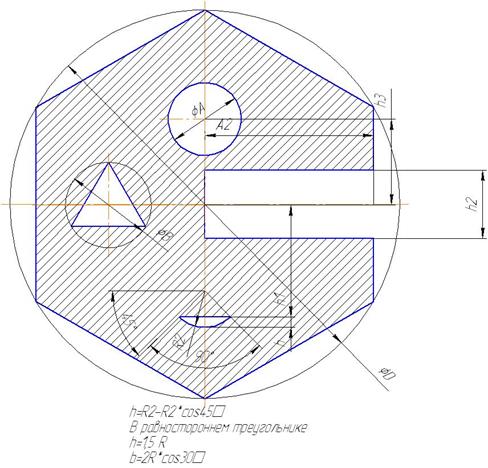
Рис. 6.7

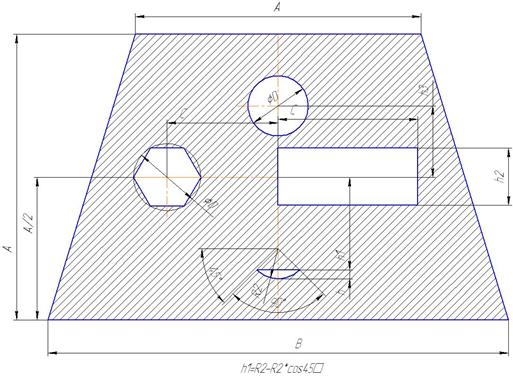
Рис. 6.8

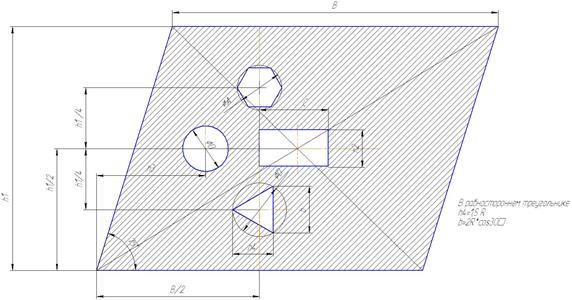
Рис. 6.9

Числовые данные для решения задачи. Таблица 6.2

Рассмотрим решение задачи на определение центра тяжести плоской фигуры, состоящей из стандартных профилей и геометрических фигур (рис.6.10).

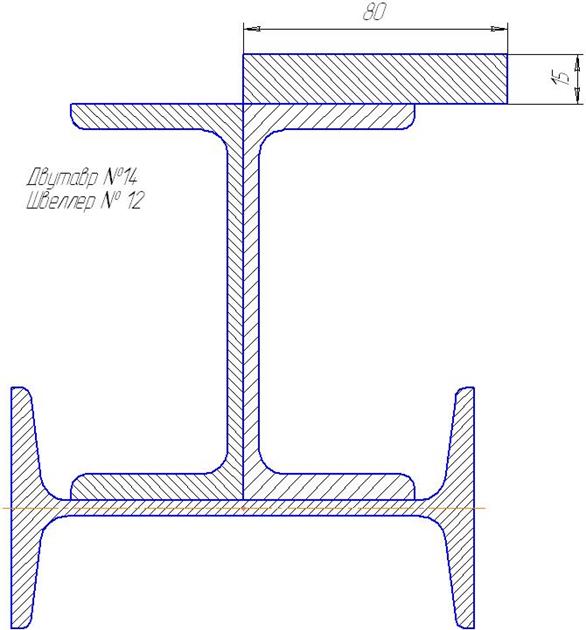
Рис. 6.10

Решение

Разобьем сечение на части, состоящие из стандартных профилей и геометрической фигуры прямоугольника (рис. 6.11):

двутавр 1 ‑ № 14;

швеллер 2 ‑ № 12;

швеллер 3 ‑ № 12;

Прямоугольник 4 с размерами b =80 мм, h =15 мм,

Принимаем оси координат, проходящие через центр тяжести двутавра 1, и определяем площади фигур и координаты центра тяжести каждой фигуры.

Двутавр 1 - № 14, y_{c 1} = 0 мм, x_{c 1} = 0 мм, A ₁ = 17, 4 см² = 1740 мм² (Площадь профиля выбираем в таблице приложения 1).

Швеллер 2 - № 12, y_{c 2} = S_дв /2+ H _шв/2 = 4, 9/2+120/2= 62, 45 мм, x_{c 2}= z ₀ = 15, 4 мм, A ₂ = 13, 3 см² = 1330 мм² (Площадь и размеры профилей выбираем в таблице приложения 1)

Швеллер 3 - № 12, y_{c 3} = S _дв/2+ H _шв/2 = 4, 9/2+120/2 = 62, 45 мм, x_{c 3} = - z₀ = -15, 4 мм, A₃ = 13, 3 см² = 1330 мм² (Площадь и размеры профилей выбираем в таблице приложения 1)

Прямоугольник 4 с размерами b =80 мм, h =15 мм,, y_{c 4} = S _дв/2+ H _шв + h /2= 4, 9/2+120+15/2= 129, 95 мм, x_{c 4} = b /2 = 40 мм, A ₄ = b h =15 80=1200 мм²

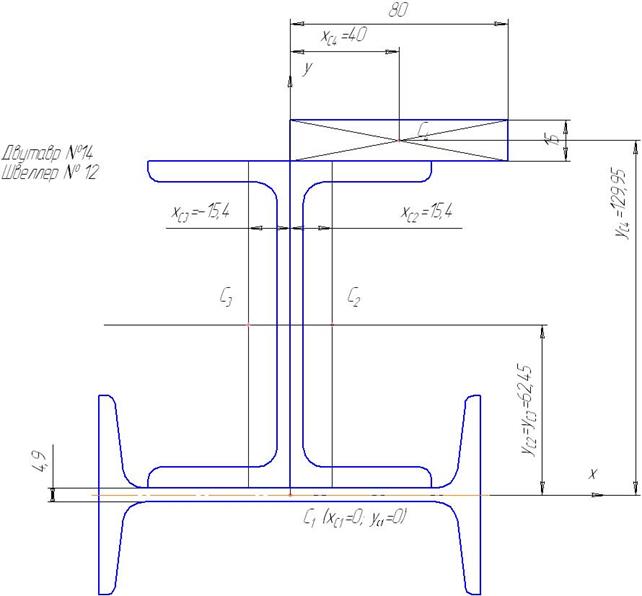
Рис. 6.11

Выполним расчет координат центра тяжести сечения по формулам:

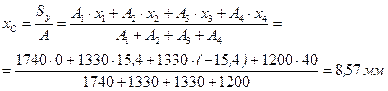
Найденный центр тяжести сечения изображен на рис.6.12.

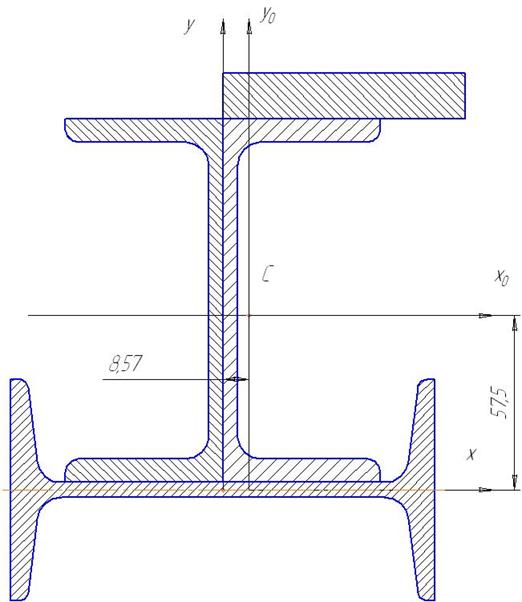
Рис. 6.12

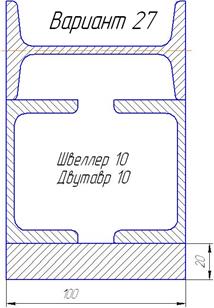
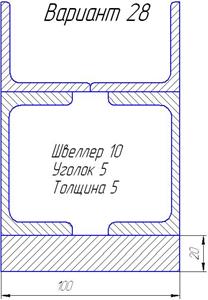
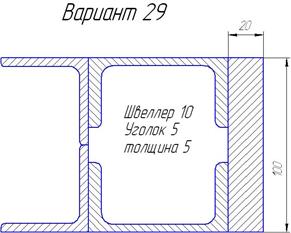
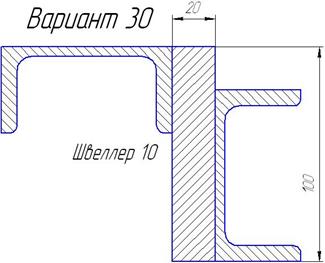
Задания для самостоятельной работы приведены в табл. 6.3

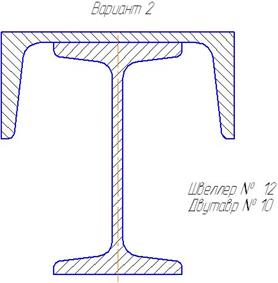
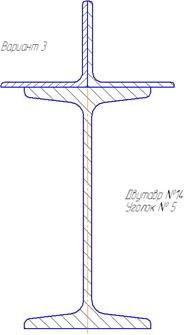
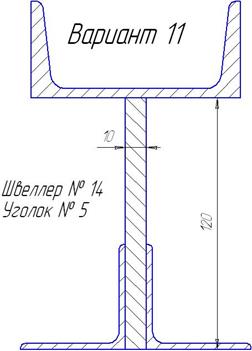
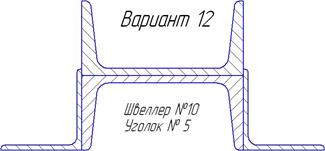
Варианты профилей для определения центра тяжести. Таблица 2.3

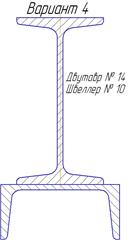
		Продолжение таблицы 6.3.
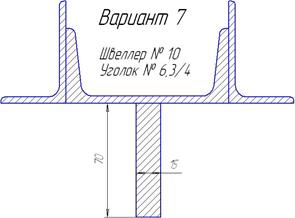
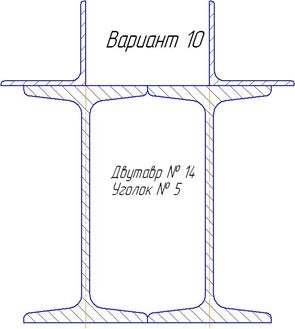
		Продолжение таблицы 6.3.
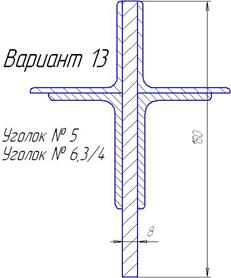
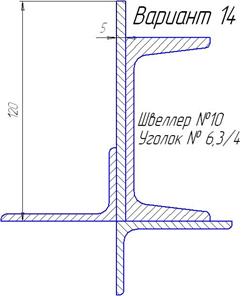
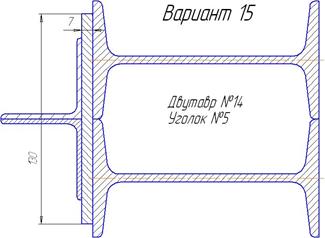
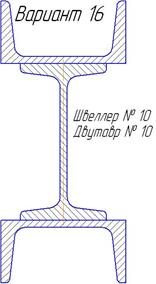
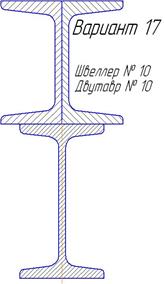
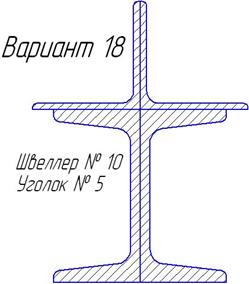
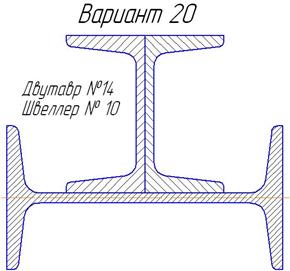
		Продолжение таблицы 6.3.
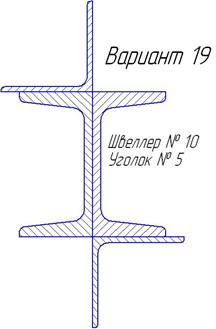
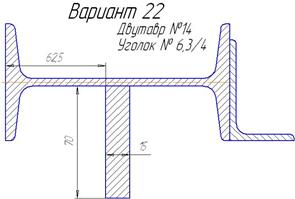
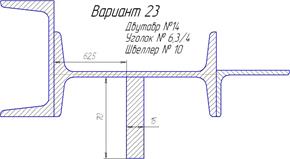
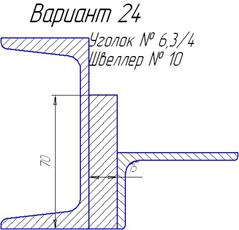
		Продолжение таблицы 6.3.
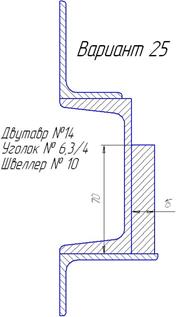
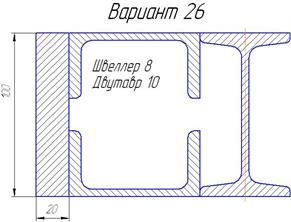