
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методи моделювання безперервних величин
|
|
Стандартний метод моделювання (метод зворотних функцій) заснований на співвідношенні функції розподілу F(x) безперервної випадкової величини X, щільності розподілу ймовірності f(x) і рівномірно розподілених (0; 1) випадкових чисел x формулою
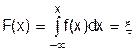
Тому, одержання випадкової величини X полягає в обчисленні виразу F-1(x) - функції, зворотної по відношенню до F(x) шляхом інтегрування, де це можливо, щільності f(x), мал.4.1.
Для показового розподілу із щільністю

Зворотні функції безперервних випадкових величин основних розподілів наведені в таблиці 5.1.
Таблиця 5.1
Алгоритми моделювання дискретних
і безперервних величин
| № | Найменування розподілу, (параметри) | Алгоритми моделювання величини X | ||
| Ряд розподілу дискретної величини X (Pi) |  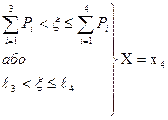
| |||
| Пуассона, (а) | 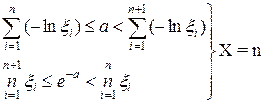
| |||
| Біноміальне (Бернуллі), (n, P) |

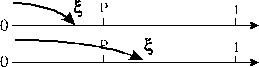
| 
| 
| |
| ||||

| 
| 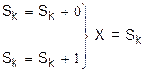
| ||
| Рівномірне, (a, b) | 
| |||
Показове, (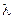 )
[експонентне] )
[експонентне]
| 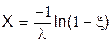
| |||
Нормальне, (m, 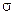 )
[Гаусса] )
[Гаусса]
| 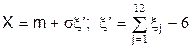
| |||
Логарифмічно нормальне, (g, 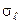 ) )
| 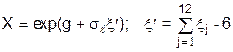
| |||
Гамма, (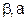 ) )
| 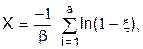 a - ціле a - ціле
| |||
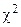 , (k)
[хі-квадрат] , (k)
[хі-квадрат]
| 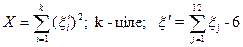
| |||
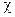 , (k) [хі] , (k) [хі]
| 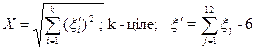
| |||
Релея, (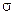 ) )
| 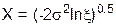
| |||
| Стьюдента, (k) | 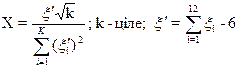
| |||
| Вейбулла, (a, b) | 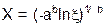
|
5.3. Порядок виконання роботи:
1. Налаштувати табличний процесор Excel для роботи з даними. Для цього переконатися в наявності вкладки Анализ данных в списку випадаючого меню кнопки рядка меню Сервис. В противному випадку зробити підключення Пакета аналіза. Для цього встановити відповідний прапорець у вікні Списка надстроек, що відкривається після вибору вкладки Надстройки кнопки рядка меню Сервис.
2. Відповідно до виданого завдання (таблиця 5.2) помістити в комірки значення параметрів безперервних і дискретних розподілів. Також помістити вихідні відповідно рівномірно (0, 1) і нормально (-3, 3) розподілені випадкові числа. Для цього встановити курсор у відповідну комірку і у рядку меню Сервис вибрати вкладку Анализ данных, інструмент аналізу - Генерация случайных чисел.
3. У вікні Генерация случайных чисел у поле з назвою Число переменных увести - 1; у поле з назвою Число случайных чисел - 100; у поле з назвою Распределение – Равномерное (Нормальное). У підвікно з назвою Параматеры для Равномерного - між 0 і 1 (для Нормального - середнє 0, стандартне відхилення 1); у поле з назвою Случайное распределение - (будь-яке число в інтервалі 1...32767); у підвікно з назвою Параметри Параметры ввода визначити початкову адресу виводу даних. По закінченні вибору параметрів полів - нажати клавішу ОК.
4. Аналогічно пункту 3 виконати моделювання для розподілів - Рівномірного, Нормального, Пуассона, Біноміального. Для розподілів - Експонентного, Логарифмічно-нормального, Релея та Вейбулла, використовуючи алгоритми моделювання (таблиця 5.1) виконати програмування комірок. Далі, використовуючи метод протягування заповнити стовпці.
5. При моделюванні Дискретного розподілу варто враховувати, що він характеризується значенням і відповідним йому інтервалом імовірності (задати самостійно). Діапазон повинен складатися із двох стовпців: лівого, що містить значення і правого, що містить ймовірності, зв'язані зі значенням у даному рядку. Сума ймовірностей повинна дорівнювати 1. Результати моделювання Дискретного розподілу помістити у відповідний стовпець.
6. Запрограмувати обчислення середнього арифметичного й стандарту по стовпцях.
7. Для кожного змодельованого масиву побудувати гістограми розподілу частот.
8. Оформити звіт з лабораторної роботи. До складу звіту лабораторної роботи №5 повинні входити: таблиця результатів моделювання заданих розподілів (роздруківка випадкових величин для 5 табличних рядків), розрахункові значення середніх арифметичного й квадратичного відхилення, гістограми розподілу частот, висновки про виконану роботу.
Експоненціальний: =-(1/F$8)*LN(1-C10).
Рівномірне: H$8+(I$8+H$8)*C10.
Нормальний: =J$8+K$8*E10.
Лог-нормальний: =EXP(L$8+M$8*E10).
Релея: =Степень(-2*степень(N$8; 2)*LN(C10); 0.5).
Вейбула: СТЕПЕНЬ(-СТЕПЕНЬ(P$8; Q$8)*LN(C10); (1/Q$8)).
Стандартное отклонение: СТАНДОТКЛП(диапазон)
Среднее: СРЗНАЧ (диапазон).
Таблиця 5.2
Вихідні дані для моделювання випадкових величин
| Значення оцінок параметрів розподілів | ||||||||||||||
| № | Дискретних | Безперервних | ||||||||||||
| Завдання | Пуас- сона | Біноміналь не | експонентне. | Рівномірне | Нормальне | Лог- нормальне | Ре-лея | Вейбулла | Хі-квад-рат | |||||
| а | n | P | l | a | b | m | s | g | s 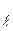
| s | a | b | k | |
| 0.51 | 0.52 | 1.2 | 7.18 | 16.59 | 12.44 | 3.53 | 4.16 | 0.41 | 1.54 | 5.34 | 2.13 | |||
| 1.63 | 0.71 | 2.5 | 12.34 | 19.08 | 93.78 | 24.18 | 3.71 | 0.26 | 0.98 | 7.18 | 1.44 | |||
| 0.35 | 0.39 | 0.7 | 59.45 | 61.73 | 243.11 | 15.95 | 2.66 | 0.12 | 2.18 | 11.12 | 0.56 | |||
| 4.29 | 0.25 | 3.8 | 97.54 | 113.37 | 6.34 | 1.28 | 4.31 | 0.39 | 0.53 | 2.68 | 4.32 | |||
| 2.47 | 0.14 | 4.2 | 107.14 | 214.58 | 42.61 | 10.37 | 3.68 | 0.32 | 1.78 | 6.53 | 1.35 | |||
| 3.82 | 0.09 | 0.03 | 37.82 | 154.12 | 38.19 | 9.72 | 2.14 | 0.11 | 2.44 | 9.81 | 0.93 | |||
| 7.63 | 0.12 | 1.84 | 1.37 | 42.17 | 68.55 | 18.31 | 5.68 | 0.56 | 3.58 | 0.51 | 2.18 | |||
| 1.28 | 0.25 | 2.17 | 43.18 | 93.18 | 110.72 | 29.44 | 4.93 | 0.86 | 1.12 | 4.73 | 1.36 | |||
| 0.86 | 0.88 | 0.93 | 17.46 | 28.34 | 18.72 | 3.68 | 2.69 | 0.53 | 0.62 | 5.18 | 0.68 | |||
| 5.47 | 0.65 | 1.84 | 51.41 | 101.37 | 25.55 | 6.47 | 3.98 | 0.68 | 4.72 | 3.64 | 0.72 |
Контрольні запитання
1)Що розуміють під моделюванням випадкової величини?
2)На чому заснований стандартний метод моделювання (метод зворотних функцій)?
3) що варто враховувати при моделюванні дискретного випадкового процесу?
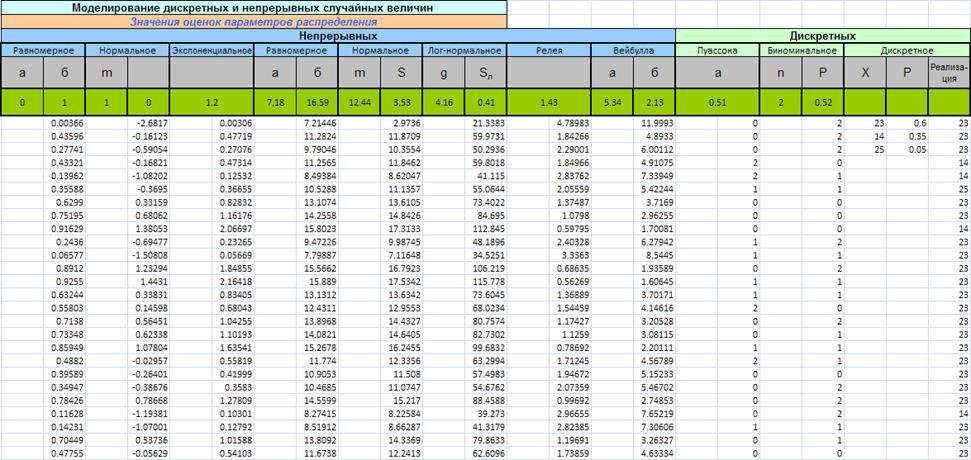

Рис.1 Приклад виконання лабораторної роботи
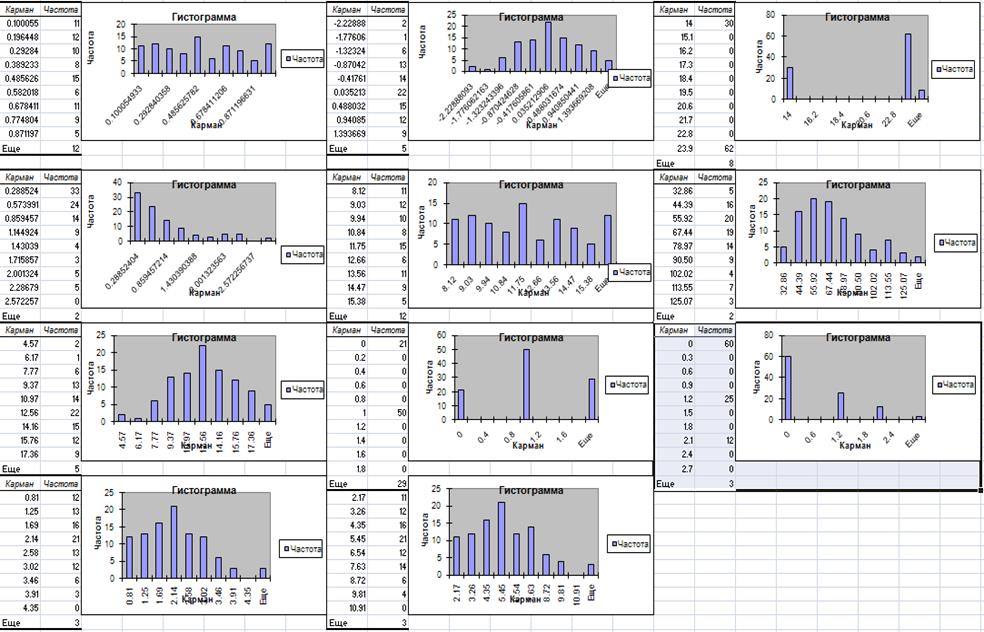
Рис.2 Приклад виконання лабораторної роботи