Критерий Чоу

Одним из нетрадиционных методов линеаризации нелинейных регрессионных моделей является разбиение всего множества наблюдений на несколько частей, каждую из которых можно аппроксимировать линейной зависимостью. Может оказаться так, что линейные регрессии для подвыборок окажутся более эффективными, чем общая нелинейная модель регрессии. Проверка такого утверждения осуществляется с помощью теста или критерия Чоу.

Пусть общая выборка имеет объем n. Через S обозначим сумму квадратов отклонений 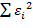для общей нелинейной регрессии. Разобьем общую выборку на две подвыборки объемами n₁ и n₂ соответственно (n₁ + n₂ = n) и построим для каждой из подвыборок частные линейные уравнения регрессии. Через S₁ и S₂ обозначим суммы квадратов отклонений для каждой из подвыборок.

Для определения значимости частных регрессионных моделей используется критерий Фишера. В этом случае выдвигается основная гипотеза о том, что качество общей регрессионной модели лучше качества частных регрессионных моделей, или подвыборок. Альтернативная гипотеза утверждает, что регрессионный анализ отдельных самостоятельных частей выборки дает результат лучше, чем регрессионный анализ выборки в целом. Наблюдаемое значение F -критерия определяется по формуле

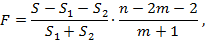
где S - S₁ - S₂ - величина, характеризующая улучшение качества модели регрессии после разделения ее на подвыборки; m - количество факторных переменных; п - объем общей выборочной совокупности.

Критическое значение F -критерия определяется по таблице распределения Фишера в зависимости от уровня значимости α и двух степеней свободы: k₁ = m + 1 и k₂ = п - 2т - 2. Если наблюдаемое значение F -критерия больше критического (F > F_табл), то основная гипотеза отклоняется, и качество частных регрессионных моделей превосходит качество общей модели регрессии. Если наблюдаемое значение F- критерия меньше критического (F < F_табл), то основная гипотеза принимается, и аппроксимировать отдельные подвыборки линейной зависимостью не имеет смысла.