Метод наименьших квадратов для нелинейных регрессионных моделей

Метод наименьших квадратов можно применять к нелинейным регрессионным моделям только в том случае, если возможна их линеаризация, т.е. они нелинейны по факторным переменным или нелинейны по параметрам, но внутренне линейны.

Рассмотрим применение МНК для определения неизвестных параметров уравнения параболической зависимости следующего вида:

y_i = β ₀ + β ₁x_i + β ₂x²_i + ε _i

Данный полином второго порядка (или второй степени) является нелинейным по факторным переменным x_i. Для нахождения неизвестных параметров уравнения регрессии β ₀, β ₁, β ₂ необходимо минимизировать с помощью МНК функцию Q:

n n

Q = Σ (y_i - y_{x i})²= Σ (y_i - β ₀ - β ₁x_i - β ₂x²_i)² → min

i =1 i =1

Процесс минимизации функции сводится к вычислению частных производных этой функции по каждому из оцениваемых параметров. Составим систему уравнений для данной функции Q, не пользуясь при этом методом замен:

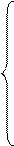дQ = -2Σ (y_i - β ₀ - β ₁x_i - β ₂x²_i) = 0

дβ ₀

дQ = -2Σ (y_i - β ₀ - β ₁x_i - β ₂x²_i) x_i = 0

дβ ₁

дQ = -2Σ (y_i - β ₀ - β ₁x_i - β ₂x²_i) x²_i = 0

дβ ₂

После элементарных преобразований данной системы уравнений получим

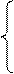nβ ₀ + β ₁ Σ x_i + β ₂ Σ x²_i = Σ y_i

β ₀ Σ x_i + β ₁ Σ x²_i + β ₂ Σ x³_i = Σ x_i y_i

β ₀ Σ x²_i + β ₁ Σ x³_i + β ₂ Σ x⁴_i = Σ x²_i y_i

Данная система является системой нормальных уравнений относительно параметров β ₀, β ₁, β ₂ для параболической зависимости y_i = β ₀ + β ₁x_i + β ₂x²_i + ε _i. Эта система является квадратной, т.е. количество уравнений равняется количеству неизвестных переменных. Коэффициенты β ₀, β ₁, β ₂ можно найти с помощью метода Гаусса, если свести систему нормальных уравнений к линейному виду с помощью метода замен.

В общем случае полинома п-й степени

y_i = β ₀ + β ₁x_i + β ₂x²_i + … +β _nxⁿ_i + ε _i.

Для нахождения неизвестных коэффициентов уравнения регрессии с помощью МНКнеобходимо минимизировать функцию Q следующего вида:

n n

Q = Σ (y_i - y_{x i})²= Σ (y_i - β ₀ - β ₁x_i - β ₂x²_i - … - β _nxⁿ_i)² → min

i =1 i =1

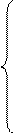Тогда систему нормальных уравнений можно записать таким образом:

Σ y_i =β ₀ n + β ₁ Σ x_i + β ₂ Σ x²_i + … + β _n Σ xⁿ_i

Σ y_i x_i = β ₀ Σ x_i + β ₁ Σ x²_i + β ₂ Σ x³_i + … + β _n Σ xⁿ⁺¹_i

………………………………………………………………

Σ y_i x^n-1_i = β ₀ Σ x^n-1_i + β ₁ Σ xⁿ_i + β ₂ Σ xⁿ⁺¹_i + … + β _n Σ x^2n-1_i

Σ y_i xⁿ_i = β ₀ Σ xⁿ_i + β ₁ Σ xⁿ⁺¹_i + β ₂ Σ xⁿ⁺²_i + … + β _n Σ x²ⁿ_i

Решением данной системы будут являться оценки коэффициентов регрессионной зависимости, выраженной полиномом п-го порядка.

Метод Гаусса применяется в большинстве случаев для решения систем линейных уравнений, когда число неизвестных параметров не совпадает с количеством уравнений. Однако его используют и для решения квадратных систем линейных уравнений.

Основная идея решения системы линейных уравнений методом Гаусса заключается в том, что исходную систему из т линейных уравнений с п неизвестными переменными необходимо преобразовать к треугольному виду. Для этого в одном из уравнений системы оставляют все неизвестные переменные. В другом сокращают одну из неизвестных переменных для того, чтобы их число стало (п - 1). В следующем уравнении убирают две неизвестные переменные, чтобы их число уже было (п - 2). В конце данного процесса система примет треугольный вид: первое уравнение содержит все, а последнее - только (п - т) неизвестных, которые называются базисными. Остальные переменные называются свободными. Дальнейшее решение сводится к выражению свободных неизвестных переменных через базисные и получению общего решения системы линейных уравнений. Для осуществления базисного решения системы линейных уравнений свободные переменные приравнивают к нулю.