
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Оценка существенности нелинейной регрессии
|
|
Если нелинейное по факторным переменным уравнение регрессии с помощью метода замен можно свести к парному линейному уравнению регрессии, то на это уравнение будут распространяться все методы проверки гипотез для парной линейной зависимости.
Проверка гипотезы о значимости нелинейной регрессионной модели в целом осуществляется через F-критерий. Выдвигается основная гипотеза Но о незначимости коэффициента детерминации для нелинейных форм связи, т.е. о незначимости полученного уравнения регрессии:
Но: R2= 0.
Альтернативной является обратная гипотеза Н1 о значимости построенного уравнения регрессии:
Н1: R2 ≠ 0.
Наблюдаемое значение F-критерия вычисляется по формуле
Fнабл = R2(п - l)
( 1 -R2)(l- 1),
где п - объем выборочной совокупности; l - число оцениваемых параметров по выборочной совокупности.
Критическое значение рассматриваемого критерия Fкрит вычисляется по таблице распределения Фишера в зависимости от уровня значимости α и числа степеней свободы k1 = l- 1 и k2 = п-l. Если наблюдаемое значение F-критерия больше критического Fнабл > Fкрит, то основная гипотеза отклоняется, следовательно уравнение нелинейной регрессии является значимым. Если наблюдаемое значение F-критерия меньше критического (Fнабл < Fкрит), то основная гипотеза принимается, и уравнение нелинейной регрессии признается незначимым.
Если существует возможность выбора между линейной и нелинейной регрессионными моделями при изучении конкретной зависимости между переменными, то предпочтение всегда отдается более простой линейной форме связи. Проверить предположение о вероятной линейной зависимости между изучаемыми переменными можно с помощью линейного коэффициента детерминации r2 и индекса детерминации для нелинейных форм связи R2.
Выдвигается основная гипотеза Но о линейной зависимости между переменными. Альтернативной является гипотеза о их нелинейной связи. Проверка этих гипотез осуществляется с помощью t-критерия Стьюдента. Наблюдаемое значение t-критерия
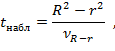
где 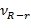 - величина ошибки разности (R2 - r2), вычисляемая по формуле
- величина ошибки разности (R2 - r2), вычисляемая по формуле
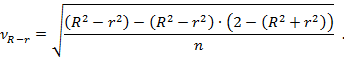
Критическое значение рассматриваемого критерия tкрит определяется по таблице распределения Стьюдента в зависимости от уровня значимости α и числа степеней свободы (п – l – 1 ), где l - число оцениваемых параметров β i в регрессионной модели. Если наблюдаемое значение t-критерия больше критического (tнабл > tкрит), то основная гипотеза отклоняется и между изучаемыми переменными существует нелинейная взаимосвязь. Если наблюдаемое значение t-критерия меньше критического (tнабл < tкрит), то зависимость между переменными может быть аппроксимирована линейным регрессионным уравнением.