Пуазейль формуласы.

Радиусы R тү тіктен тұ тқ ыр сығ ылмайтын сұ йық ақ сын. Ток сызық тары тү тік ө сіне параллель. Егер токтың кез келген шексіз жің ішке тү тігін бө ліп алсақ, онда сығ ылмаушылық шартынын ағ ыстың жылдамдығ ы ток тү тігінің барлық жерінде бірдей болатындығ ы шығ ады. Тү тік бойында сұ йық тың қ озғ алысы ө згере алмайды. Бірақ ол тү тік радиусының ө згеруі нә тижесінде ө згере алады. Осылайша, сұ йық тың жылдамдығ ы r радиусының функциясы болып табылады.

Тү тік ө сін Х ө сі деп алайық. Ол ағ ыс бағ ытымен бірдей. Тү тіктен кез келген шексіз қ ысқ а ұ зындығ ы dx, радиусы rболатын цилиндр бө лікті кесіп алайық.

Цилиндрдің қ озғ алыс бағ ытындағ ы бү йір бетіне жанама ішкі ү йкеліс кү ші ә сер етеді. Бұ дан басқ а сол бағ ыттағ ы цилиндрдің табанына 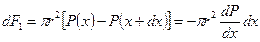тең қ ысымдар айырымы кү ші ә сер етпек.

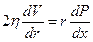
болғ андық тан, тұ рақ ты ағ ыс кезінде бұ л екі кү штің қ осындысы нө лге тең.

V(r) жылдамдығ ы жә не туындысы х-ң ө згеруіне қ арамастан, олар тұ рақ ты болады. Сондық тан 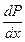туындысы да тұ рақ ты болуы керек. Бұ л туынды 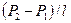-ге тең. Мұ ндағ ы -сұ йық тың тү тікке кірердегі қ ысымы, ал 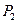- шығ ардағ ысы; 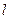-тү тік ұ зындығ ы. Нә тижесінде мына тең деуге келеміз:

(1)

Оны интегралдасақ,

С тұ рақ тысы тү тік қ абырғ асына байланысты, яғ ни r=R кезінде V жылдамдығ ы 0-ге тең болуы керек. Ол мынаны береді:

(2)

V жылдамдығ ы тү тік ө сінде максимум болады:

(3)

Осьтен шығ у кезінде жылдамдық параболалық заң бойынша ө згереді.

Сұ йық шығ ыны - ә р секунд сайын тү тіктің кө денең қ имасы арқ ылы ағ атын сұ йық мө лшері.

Тү тіктің ішкі радиусы r жә не сыртқ ысы r+dr болатын ауданынан ә р секундта ағ ып ө тетін сұ йық тың массасы:

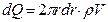
тең. Осығ ан V жылдамдық тың ө рнегін қ ойып, оны интегралдасақ, онда сұ йық шығ ыны табылады:

немесе

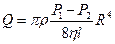(4)

Сұ йық шығ ыны 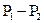қ ысымдар айырымына жә не тү тік радиусының 4-дә режесіне тура пропорционал, тү тік ұ зындығ ына жә не сұ йық тың тұ тқ ырлық коэффициентіне кері пропорционал. Бұ л формула Пуазейль формуласы деп аталады.

Пуазейль формуласы ламинар ағ ыс ү шін арналғ ан, трубуленттік қ озғ алыс ү шін бұ л формула жарамайды.

Ә р секунд сайын тү тіктің кө лденең қ имасы арқ ылы ө тетін сұ йық ағ ысының кинетикалық энергиясы:

V-ң мә нін қ ойып, оны интегралдасақ:

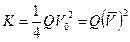(5)

Ә р секунд сайын сұ йық тың 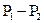қ ысымдар айырымына жұ мсалатын жұ мыс:

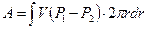
Арқ ылы есептеледі. Немесе

(6)

Тұ рақ ты қ озғ алыс кезінде сұ йық тың кинетикалық энергиясы ө згермегендіктен осындай мә нге ие, бірақ қ арама-қ арсы таң бада жұ мысты ішкі ү йкеліс кү ші жасайды:

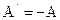
(3)-формула бойынша қ ысымдар айырымының екректі мә нін қ оямыз:

(7)

Осы формула арқ ылы қ ай кезде тұ тқ ырлық кү шін ескермеуге болатындығ ын, қ ай кезде Бернулли тең деуін қ олдануғ а болатындығ ын біле аламыз.

Бұ л ү шін сұ йық тың тұ тқ ырлық кү шінің ә серімен пайда болғ ан кинетикалық энергиясы сұ йық тың ө зінің кинетикалық энергиясынан ө те аз болуы керек. Яғ ни, 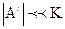. Бұ л мынадай шартқ а ә келеді:

(9)

Мұ ндағ ы 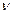-кинематикалық тұ тқ ырлық, яғ ни

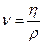(10)

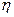-динамикалық тұ тқ ырлық.

Пуазейль заң дары жалпы тү рде ө лшемдік ә дістермен алынғ ан. Бұ л ә дістің ерекшелігі – цилиндр тү тікке ғ ана емес, сонымен қ атар кез келген кө лденең қ имасы тү зусызық ты болатын тү тіктерге де қ олданылады. Барлық тү тіктердің нормаль колденең қ ималары геометриялық жағ ынан ұ қ сас болуы керек. Бұ л қ ималар бір-бірінен тек ө лшемдерімен ерекшеленеді. Ә рбір кө лденең қ имағ а сипаттамалық ө лшем беруге болады. Оғ ан мысалы, периметр жә не ауданнан алынғ ан квадрат тү бірді алуғ а болады.

Геометриялық ұ қ састық тары бар тү тіктердің кө лденең қ ималарын тү зу сызық ты етіп қ ырқ ып, екіге бө луге болады. Бұ л қ ырқ ылғ ан жердің ұ зындығ ы сипаттамалық ө лшем болып табылады.

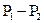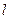Сұ йық тың тұ рақ ты ламинар ағ ысында тұ тқ ырлық кү ші қ ысым градиентіне тең болады. Қ ысымдар айырымы жә не -тү тіктің ұ зындығ ы 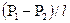комбинациясына кіргендіктен бұ л градиенттер қ озғ алыс тең деуіне де кіреді.Сұ йық ү деусіз қ озғ алғ андық тан, ағ ыс сипаты сұ йық тығ ыздығ ына тә уелсіз болады.

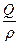Тығ ыздық пен Q сұ йық шығ ыны комбинациясына келеді. Бұ л ә р секунд сайын тү тіктің кө лденең қ имасы арқ ылы ө ткен сұ йық тың кө леміне тең. Мұ нда сұ йық тұ тқ ырлығ ын 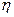жә не тү тіктің сипаттамалық ө лшемін а қ осып, тө рт ө лшем аламыз:

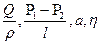
Олардың арасында функционалды байланыс бар. а -ң орнына S кө лденең қ има ауданын қ ойса болады.

Қ арастырып отырғ ан ө лшемдерден бір ғ ана тә уелсіз ө лшемсіз комбинация қ ұ рылады:

Мұ ндай комбинация тұ рақ ты болуы керек. Бұ л тұ рақ тыны С-ң кө мегімен ө рнектесек,

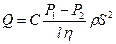(11)

Бұ л формулада Пуазейльдің барлық заң дары бар. Бұ л кез келген кө лденең қ имадағ ы тү зусызық ты тү тік ү шін арналғ ан (4)-формуланың жалпыланғ ан тү рі болып табылады.

С тұ рақ тысы тү тіктің кө лденең қ имасының формасына тә уелді жә не ол ө лшемдік ә діспен анық талмайды. Оны табу ү шін тә жірибеге немесе динамикалық ә дістерге арқ а сү йеу керек. Яғ ни қ озғ алыс тең деуін интегралдау керек.