Сложные проценты

В практических расчетах в основном применяют дискретные проценты, т.е. проценты, начисляемые за фиксированные одинаковые интервалы времени (год, полугодие, квартал и т. д.). Время - дискретная переменная. В некоторых случаях - в доказательствах и расчетах, связанных с непрерывными процессами, возникает необходимость в применении непрерывных процентов. Рассмотрим формулу сложных процентов:

S = P(1 + i)ⁿ. (6.16)

Здесь P - первоначальная сумма, i - ставка процентов (в виде десятичной дроби), S - сумма, образовавшаяся к концу срока ссуды в конце n -го года. Рост по сложным процентам представляет собой процесс, развивающийся по геометрической прогрессии. Присоединение начисленных процентов к сумме, которая служила базой для их определения, часто называют капитализацией процентов. В финансовой практике часто сталкиваются с задачей, обратной определению наращенной суммы: по заданной сумме S, которую следует уплатить через некоторое время n, необходимо определить сумму полученной ссуды P. В этом случае говорят, что сумма S дисконтируется, а проценты в виде разности S - P называются дисконтом. Величину P, найденную дисконтированием S, называют современной, или приведенной, величиной S. Имеем:

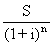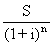P = ; P = = 0.

Таким образом, при очень больших сроках платежа современная величина последнего будет крайне незначительна.В практических финансово-кредитных операциях непрерывные процессы наращения денежных сумм, т. е. наращения за бесконечно малые промежутки времени, применяются редко. Существенно большее значение непрерывное наращение имеет в количественном финансово-экономическом анализе сложных производственных и хозяйственных объектов и явлений, например, при выборе и обосновании инвестиционных решений. Необходимость в применении непрерывных наращений (или непрерывных процентов)определяется прежде всего тем, что многие экономические явления по своей природе непрерывны, поэтому аналитическое описание в виде непрерывных процессов более адекватно, чем на основе дискретных. Обобщим формулу сложных процентов для случая, когда проценты начисляются m раз в году:

S =P (1 + i/m) ^mn.

Наращенная сумма при дискретных процессах находится по этой формуле, здесь m - число периодов начисления в году, i - годовая или номинальная ставка. Чем больше m, тем меньше промежутки времени между моментами начисления процентов. В пределе при m → ∞ имеем:

S = 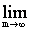P (1 + i/m) ^mn = P 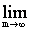((1 + i/m) ^m) ⁿ.

Поскольку 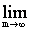(1 + i/m) ^m = e ⁱ, то  S = P e ⁱⁿ.

При непрерывном наращении процентов применяют особый вид процентной ставки - силу роста, которая характеризует относительный прирост наращенной суммы в бесконечно малом промежутке времени. При непрерывной капитализации процентов наращенная сумма равна конечной величине, зависящей от первоначальной суммы, срока наращения и номинальной ставки процентов. Для того, чтобы отличить ставки непрерывных процентов от ставки дискретных процентов, обозначим первую через , тогда S = Pe .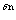

Сила роста  представляет собой номинальную ставку процентов при m→ ∞. Множитель наращения рассчитывается с помощью ЭВМ или по таблицам функции.