Приложения.. 69

Глава 2. ОБЩИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ 7

Содержание заданий, выбор вариантов. 7

Требования к выполнению и оформлению контрольной работы.. 7

Защита контрольной работы.. 8

Глава 3. СТАТИКА.. 9

Порядок решения задач по статике на равновесие. 9

Проецирование силы на ось и на плоскость. 9

Основные типы связей и их реакции. 10

Принцип освобождаемости от связей. 10

Типы связей. 10

Теория моментов сил. 12

Момент силы относительно точки. 12

Момент силы относительно оси. 14

3.5. С -1. Произвольная плоская система сил.
Определение реакций связей сплошной конструкции. 14

Условия равновесия произвольной плоской системы сил. 15

Пример С-1. 16

3.6. С-2. Произвольная пространственная система сил.
Определение реакций связей. 19

3.6.1. Условия равновесия произвольной пространственной
системы сил. 19

Пример С-2. 25

Глава 4. КИНЕМАТИКА.. 27

Кинематика точки. Способы задания движения точки. 27

4.1.1. К -1. Определение скорости и ускорения точки по заданным уравнениям её движения. 30

Пример К-1. 31

Плоскопараллельное (плоское) движение твердого тела. 32

Скорость точки при плоском движении. 33

Теорема о проекциях скоростей. 33

Теорема о распределении скоростей. 33

Ускорение точки тела при плоском движении. 34

4.2.5. К-2. Определение скоростей и ускорений точек
многозвенного механизма. 35

Пример К-2. 36

Сложное движение точки. 45

4.3.1. Основные определения и правила в теории сложного
движения точки. 46

4.3.2. К-3. Определение абсолютной скорости и абсолютного
ускорения точки. 47

4.3.3. Пример К– 3. 47

Глава 5. ДИНАМИКА.. 53

5.1. Динамика точки. Дифференциальные уравнения
движения точки. Основные задачи динамики. 53

Д -1. Динамика материальной точки. 53

Пример Д -1. 54

Теорема об изменении кинетической энергии материальной системы 58

5.3.1. Формулы для подсчёта кинетической энергии твердого
тела в различных видах его движения. 58

Примеры вычисления работы сил. 59

5.3.3. Д -2. Применение теоремы об изменении кинетической
энергии к изучению движения механической системы.. 60

Пример Д -2. 60

Литература.. 68

Приложения.. 69

Глава 1. СОДЕРЖАНИЕ ДИСЦИПЛИНЫ И ТРЕБОВАНИЯ К УРОВНЮ ЕЁ ОСВОЕНИЯ

«Теоретическая механика» – одна из фундаментальных естественнонаучных дисциплин физико-математического цикла. На материале теоретической механики базируются дисциплины (или разделы дисциплин): «Сопротивление материалов», «Прикладная механика», «Теория механизмов и машин», «Детали машин и основы конструирования», «Гидравлика», а также большое число специальных инженерных дисциплин, посвященных изучению динамики и управления машин, используемых в различных отраслях экономики. Изучение теоретической механики дает фундаментальные знания, на основе которых будущий специалист сможет самостоятельно решать производственные и научные задачи.

Теоретическая механика делится на три раздела: статику, кинематику и динамику.

Статика изучает условия, при которых механическое взаимодействие тел не нарушает их относительного покоя или равномерного прямолинейного поступательного движения.

Кинематика изучает движение объектов с геометрической точки зрения, то есть без учета их масс и сил, приложенных к ним.

Динамика изучает движение материальных объектов с учетом действующих на них сил.

В процессе освоения дисциплины студент должен получить представление о предмете теоретической механики, возможностях ее аппарата и границах применимости ее моделей, прибрести навыки решения типовых задач по всем разделам теоретической механики.

В связи с тем, что количество аудиторного времени, выделяемого на освоение дисциплины «Теоретическая механика», различно для разных специальностей ниже сформулированы некоторые усредненные требования к уровню подготовки по данному предмету.

В результате изучения теоретической механики студент должен знать:

- основные понятия и аксиомы статики;

- основные типы связей и их реакции; принцип освобождаемости от связей;

- теорию моментов: момент силы относительно точки; момент силы относительно оси; пара сил;

- условия равновесия плоской системы сил: сходящихся, параллельных и расположенных произвольно; частные случаи этих условий;

- условия равновесия пространственной системы сил: сходящихся, параллельных и расположенных произвольно; частные случаи этих условий;

- методы нахождения реакций связей материальных систем, сочлененных из двух и более твердых тел;

- способы нахождения центров тяжести линий, фигур и тел;

- законы трения скольжения и трения качения;

- способы задания движения точки;

- уравнения различных видов движения твердого тела;

- кинематические характеристики движения тела и его точек при различных видах движения;

- как определить скорость и ускорение точки, принадлежащей твердому телу, участвующему в различных видах движения;

- теорию сложного движения точки;

- дифференциальные уравнения движения точки в различных формах;

- как следует применять дифференциальные уравнения движения точки для решения двух основных задач динамики;

- основное уравнение динамики;

- теоремы об изменении количества движения, кинетического момента и кинетической энергии материальной системы;

- теорему о движении центра масс материальной системы;

- дифференциальные уравнения поступательного, вращательного и плоскопараллельного движения твердого тела;

- теорему Штейнера-Гюйгенса;

- принцип Даламбера;

- уравнения Лагранжа второго рода;

- теорию удара.

Студент должен уметь:

- составлять уравнения равновесия свободного абсолютно твердого тела, находящегося под действием любой системы сил;

- находить положения центров тяжести фигур и тел;

- находить скорости и ускорения точек, принадлежащим телам, совершающим различные виды движения;

- составлять дифференциальные уравнения движения материальных точек и тел, участвующих в поступательном, вращательном и плоском движениях;

- вычислять кинетическую энергию многомассовой системы;

- вычислять работу сил, приложенных к твердому телу, при его поступательном, вращательном и плоском движениях;

- составлять уравнения Лагранжа второго рода для механических систем с одной степенью свободы.

Глава 2. ОБЩИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ

2.1. Содержание заданий, выбор вариантов

Контрольная работа предполагает самостоятельное решение задач по трём разделам теоретической механики по следующим темам:

1. С-1. Произвольная плоская система сил. Определение реакций связей сплошной конструкции.

2. С-2. Произвольная пространственная система сил. Определение реакций связей.

3. К-1. Кинематика точки. Определение скорости и ускорения точки по заданным уравнениям ее движения.

4. К-2. Плоскопараллельное движение твердого тела. Определение скоростей и ускорений точек многозвенного механизма.

5. К-3. Сложное движение точки. Определение абсолютной скорости и абсолютного ускорения точки.

6. Д-1. Динамика материальной точки. Интегрирование дифференциальных уравнений движения материальной точки, находящейся под действием постоянных сил.

7. Д-2. Применение теоремы об изменении кинетической энергии к изучению движения механической системы.

Каждая задача задается одним из 10 рисунков подраздела и дополнительными условиями, содержащимися в таблице. Нумерация рисунков двойная, при этом номером рисунка является цифра, стоящая после точки. Например, обозначение рис. С 1.4 означает: рисунок 4 к задаче С-1.

Чтобы определиться с заданием, Вам необходимо во всех задачах выбрать номер рисунка по предпоследней цифре шифра в Вашей зачетной книжке, а номер дополнительного условия в таблице – по последней цифре. К примеру, если «23» - две последние цифры шифра в Вашей зачетной книжке, то это означает, что номер варианта Вашего задания «23», и, следовательно, при решении любой задачи Вам необходимо взять рисунок под № 2, а дополнительные условия из строки под № 3 таблицы.

2.2. Требования к выполнению и оформлению контрольной работы

Прежде чем приступить к выполнению задачи необходимо:

1. Изучить теоретический материал по теме задания.

2. Ознакомиться с указаниями по выполнению задания.

3. Рассмотреть решение типовой задачи, предложенной в данных методических указаниях.

4. Уяснить содержание задачи, проанализировать её и найти наилучший вариант решения.

Решенные задачи оформляются на бумаге для машинописных работ формата А4 в соответствии с требованиями ЕСКД.

Примеры оформления титульного листа в РИО. Примеры выполнения и оформления задач – в основной части методических указаний.

Чертеж к задаче должен быть выполнен карандашом. Чертеж должен быть наглядным и аккуратным, его размеры должны позволять, показать все силы или векторы скоростей и ускорений и пр.; на чертеже обязательно должны быть нанесены (если этого требует решение задачи) координатные оси. Решение задач следует сопровождать пояснениями (на основании каких теорем, свойств, формул решается задача), подробно демонстрировать весь ход расчетов. Формулы и уравнения необходимо нумеровать в пределах одной задачи. Записи вести только на лицевой стороне листа. При оформлении задач следует использовать условные обозначения, приведенные в справочном приложении А. Расчеты проводить с соблюдением правил приближенных вычислений. Результаты вычислений рекомендуется заносить в таблицу ответов.

2.3. Защита контрольной работы

Выполненная и исправленная после проверки преподавателем работа подлежит «защите». Во время «защиты» контрольной работы студент должен:

- показать знание теоретического материала по разделам, относящимся к заданиям;

- объяснить и обосновать данное им решение задачи;

- уметь решать задачи по темам контрольной работы.

Глава 3. СТАТИКА

3.1. Порядок решения задач по статике на равновесие

Для решения задачи по статике на равновесие необходимо:

- выбрать объект, равновесие которого следует рассмотреть, чтобы решить задачу;

- изобразить и обозначить все активные силы и связи, действующие на объект;

- применив принцип освобождаемости от связей, заменить отброшенные связи их реакциями;

- установить, какая система сил действует на этот объект;

- применить условие равновесия для полученной системы сил и найти неизвестные.

3.2. Проецирование силы на ось и на плоскость

Проекцией силы на ось называется скалярная величина, равная произведению модуля силы на косинус угла между направлением силы и положительным направлением оси. Проекция будет положительной, если угол между направлением силы и положительным направлением оси – острый, и отрицательной, если этот угол – тупой (рис. 3.1).

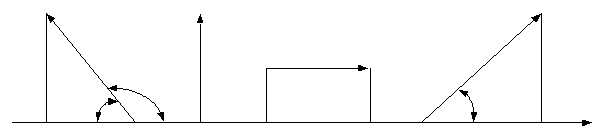
φ β 90⁰ γ l

Пр_l Пр_l Пр_l

Рис. 3.1.

Пр_l =F_1· cosβ = - F_{1 ·} cosφ; Пр_l 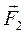=F_2· cos90⁰ = 0;

Пр_l 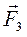=F_3· cos0⁰ = F₃; Пр_l =F_4· cosγ = F_4· cosγ.

Проекцией силы на плоскость называется векторная величина, заключенная между проекциями начала и конца вектора силы на эту плоскость (рис. 3.2).

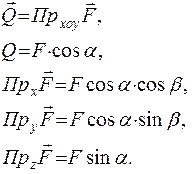
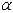
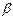
Рис. 3.2

3.3. Основные типы связей и их реакции

Тела, ограничивающие перемещение данного объекта, называются связями.

Связи реализуются в виде поверхностей, нитей, стержней и т.п.

Сила, с которой связь действует на объект, называется силой реакции связи или реакцией связи.

3.3.1. Принцип освобождаемости от связей

Любой несвободный объект можно рассматривать как свободный, если, освободив его от связей, заменить их реакциями связей.

3.3.2. Типы связей

1. Гладкая неподвижная поверхность, на которую тело М опирается точкой или линией. Реакция 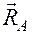направлена по нормали к этой поверхности (рис. 3.3).

2. Неподвижная точка или гладкая линия: тело М опирается на неподвижную точку или линию. Реакции 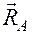, 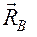направлены по нормали к линии или поверхности рассматриваемого тела (рис. 3.4).

 

 

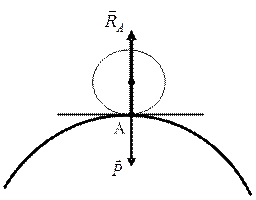
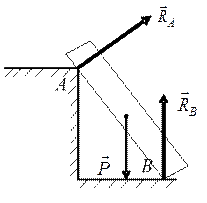
Рис. 3.3 Рис. 3.4

3. Гибкие связи (цепи, канаты, тросы). Реакции 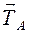, , 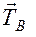направлены вдоль гибкой связи от тела М к точке подвеса (рис. 3.5).

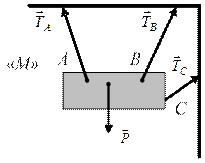
Рис. 3.5 Рис. 3.6

4. Неподвижный цилиндрический шарнир или подшипник (рис. 3.6): на неподвижный болт А надета втулка В, жестко скрепленная с телом М, причем внутренний диаметр втулки почти равен диаметру болта. Тело М может вращаться вокруг оси шарнира, перпендикулярной к плоскости рисунка. Внешние силы, действующие на тело М, должны быть перпендикулярны оси шарнира, чтобы втулка не была снята с болта. Если пренебречь трением в шарнире, то реакция неподвижного болта направлена по нормали к его цилиндрической поверхности, и, в зависимости от величин и направлений сил, приложенных к телу, может иметь любое направление в плоскости, перпендикулярной оси шарнира. Поскольку направление реакции неизвестно, то такую реакцию необходимо представить в виде двух ее составляющих: и тогда .

5. Сферический шарнир или подпятник (рис. 3.7): реакция может иметь любое направление. При решении задач реакцию необходимо разложить на три составляющие по осям прямоугольной системы координат:

 

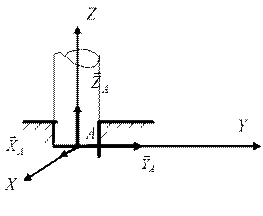
Рис. 3.7 Рис. 3.8

6. Невесомый стержень (рис. 3.8): сила реакции стержня 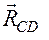направлена вдоль оси стержня.

 

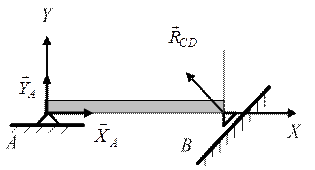
Рис. 3.9 Рис. 3.10

7. Шарнирно-подвижная опора (опора на катках) и шарнирно-неподвижная опора (рис. 3.9): реакция шарнирно-подвижной опоры 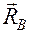перпендикулярна поверхности (плоскости) «катков»; реакция шарнирно-неподвижной опоры должна быть представлена двумя ее составляющими: .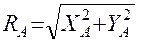

8. Жесткая заделка (рис. 3.10): реакция жесткой заделки эквивалентна силе и паре сил с моментом

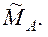
Примечание: все связи рассмотрены без учета силы трения.

 

3.4. Теория моментов сил

3.4.1. Момент силы относительно точки

Векторный момент (или вектор-момент) силы относительно точки (или центра) есть векторное произведение радиуса-вектора точки приложения силы на вектор силы: , где 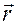– радиус-вектор точки приложения силы относительно центра, (рис. 3.11).

Вектор 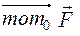перпендикулярен плоскости, в которой лежат перемножаемые векторы и направлен в ту сторону, откуда виден воображаемый поворот вектора 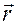к вектору (до их совмещения) на наименьший угол против хода часовой стрелки (рис. 3.11).

Рис. 3.11.

Модуль момента силы относительно точки равен произведению модулей радиуса-вектора точки приложения силы и вектора силы на синус угла между этими векторами или произведению модуля силы на плечо силы:

.

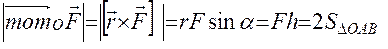Плечо силы относительно точки (или центра) – длина перпендикуляра, опущенного из моментной точки О (или центра) на линию действия силы.

Скалярный момент силы относительно точки есть произведение модуля силы на плечо, взятое со знаком «плюс», если сила стремится повернуть тело вокруг моментной точки (или центра) против часовой стрелки, и со знаком «минус» - в противном случае (рис. 3.12):

; .

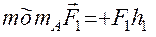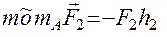Рис. 3.12

Свойства момента силы относительно точки:

1. Момент силы относительно точки не изменится, если силу переносить вдоль линии ее действия.

2. Момент силы относительно точки не изменится, если моментную точку переносить вдоль линии, параллельной линии действия силы.

3. Момент силы относительно точки равен нулю, если моментная точка принадлежит линии действия силы: , так как h₃ =0 относительно точки А (рис. 3.12).

4. , если силы принадлежат одной линии действия.

3.4.2. Момент силы относительно оси

Момент силы относительно оси есть проекция на эту ось момента силы, вычисленного относительно точки, лежащей на оси: 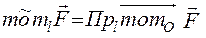( рис 3.13).

Рис. 3.13 Рис. 3.14

Чтобы вычислить момент силы относительно оси, надо спроецировать эту силу на плоскость, перпендикулярную оси, найти модуль момента проекции силы относительно точки пересечения оси с плоскостью, а затем присвоить полученному значению знак «плюс», если сила стремится повернуть тело вокруг данной оси против часовой стрелки и «минус» - в противном случае: ( рис.3.14 ).

Свойства момента силы относительно оси:

1. Момент силы относительно оси не зависит от выбора точки на оси.

2. Момент силы относительно оси равен нулю, если линия действия силы пересекает данную ось или сила параллельна оси, то есть в том случае, когда ось и сила лежат в одной плоскости.

Главный момент силы относительно некоторого центраО есть сумма моментов всех сил системы относительно этого центра: .

Главный момент силы относительно некоторой оси есть сумма моментов всех сил системы относительно этой оси: .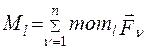

3.5. С -1. Произвольная плоская система сил.
Определение реакций связей сплошной конструкции