
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение. 1. Анализ задания: точка М совершает сложное движение, так как она движется по пластине вдоль прямой BD и вместе с пластиной
|
|
1. Анализ задания: точка М совершает сложное движение, так как она движется по пластине вдоль прямой BD и вместе с пластиной, вращающейся вокруг неподвижной оси, перпендикулярной плоскости пластины.
2. Выберем две системы координат: неподвижную с началом координат в точке О1 и подвижную с началом координат в точке М:
- абсолютное движение точки М – её движение относительно неподвижной системы координат O1X1Y1;
- относительное движение точки М – её движение относительно подвижной системы координат ОXY, то есть движение точки по прямой BD; траекторией является прямая;
- переносное движение – движение подвижной системы координат относительно неподвижной, то есть вращение пластины относительно оси, ей перпендикулярной.
3. Положение точки на прямой BD определяется расстоянием s=AM=18sin(π t/4) см, при t1=2/3 с, s=AM= 9 см.
4. Абсолютную скорость точки М найдем как геометрическую сумму относительной и переносной скоростей: 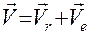 .
.
5. Относительная скорость точки М равна  (см/c), при t1=2/3 с Vr = 12, 24 (см/c). Вектор относительной скорости направлен в сторону возрастания s, так как Vr › 0.
(см/c), при t1=2/3 с Vr = 12, 24 (см/c). Вектор относительной скорости направлен в сторону возрастания s, так как Vr › 0.
6. Определим переносную скорость точки М, мысленно остановив движение точки по прямой BD. В переносном движении точка М описывает окружность радиуса R= ОМ:
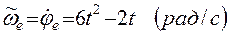 , при t1=2/3 с
, при t1=2/3 с 
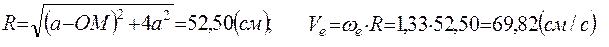
Вектор переносной скорости направлен по касательной к окружности в сторону вращения пластины.
7. Найдем модуль абсолютной скорости по формуле: 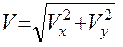 , где
, где
Vx=Ve - Vr∙ cosβ =69, 82-12, 24·0, 95=58, 17 (см/c);
Vy= - Vr∙ sinβ = - 12, 24∙ 0, 31=-3, 73(см/c);
V=58, 29 (см/c).
8. Абсолютное ускорение точки равно геометрической сумме относительного, переносного ускорений и ускорения Кориолиса:
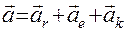 или
или 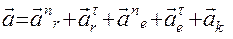 .
.
9. Для определения относительного ускорения точки М мысленно остановим подвижную систему координат и вычислим относительное касательное ускорение:  , при t1=2/3 с
, при t1=2/3 с
аτ r= -5, 55 (cм/c2).
Знак «минус» показывает, что вектор относительного касательного ускорения направлен в сторону отрицательных значений S: движение замедленное.
Относительное нормальное ускорение равно нулю, поскольку движение точки М вдоль BD – прямолинейное.
10. Переносное касательное ускорение определяем, мысленно остановив точку М в подвижной системе координат:

Знаки угловой скорости и углового ускорения переносного вращения одинаковы, и, следовательно, движение является ускоренным, направления векторов угловой скорости и углового ускорения совпадают. Векторы касательного ускорения и скорости в переносном движении направлены в одну сторону. Вектор нормального ускорения переносного вращательного движения направлен по радиусу к центру окружности, которую описывает тот
пункт подвижной системы координат, с которым совпадает точка М в данный момент времени.
11. Определяем модуль ускорения Кориолиса:  , где α – угол между вектором относительной скорости и вектором угловой переносной скорости (оси вращения). В нашем случае это угол равен 900, так как ось вращения перпендикулярна плоскости пластины, в которой расположен вектор относительной скорости. В момент времени t1=2/3 с аk = 32, 56 (cм/c2). Направление вектора ускорения Кориолиса находим по правилу Жуковского: так как вектор относительной скорости лежит в плоскости вращения, перпендикулярной оси вращения, то, повернув его на 900 в направлении угловой переносной скорости, то есть против хода часовой стрелки, найдем направление вектора ускорения Кориолиса.
, где α – угол между вектором относительной скорости и вектором угловой переносной скорости (оси вращения). В нашем случае это угол равен 900, так как ось вращения перпендикулярна плоскости пластины, в которой расположен вектор относительной скорости. В момент времени t1=2/3 с аk = 32, 56 (cм/c2). Направление вектора ускорения Кориолиса находим по правилу Жуковского: так как вектор относительной скорости лежит в плоскости вращения, перпендикулярной оси вращения, то, повернув его на 900 в направлении угловой переносной скорости, то есть против хода часовой стрелки, найдем направление вектора ускорения Кориолиса.
12. Модуль абсолютного ускорения точки М найдем, предварительно спроецировав обе части векторного равенства, представленного выше, на координатные оси:

Ответ: V=58, 29 см/c, a=316, 13 см/c2.
Глава 5. ДИНАМИКА
5.1. Динамика точки. Дифференциальные уравнения движения точки. Основные задачи динамики