
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Интегрирование дифференциальных уравнений движения материальной точки, находящейся под действием постоянных сил
|
|
Дано: груз D массой m, получив в точке А начальную скорость v0, движется в изогнутой трубе АВС, расположенной в вертикальной плоскости; участки трубы или оба наклонные, или один горизонтальный, а другой наклонный (рис. Д 1.0-Д1.9, табл. Д -1).
На участке АВ на груз кроме силы тяжести действуют постоянная сила 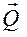 (ее направление показано на рисунках) и сила сопротивления среды
(ее направление показано на рисунках) и сила сопротивления среды 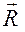 , зависящая от скорости
, зависящая от скорости  груза (направлена против движения); трением груза о трубу на участке АВ пренебречь.
груза (направлена против движения); трением груза о трубу на участке АВ пренебречь.
В точке В груз, не изменяя своей скорости, переходит на участок ВС трубы, где на него кроме силы тяжести действуют сила трения (коэффициент трения о трубу f=0, 2) и переменная сила  , проекция которой
, проекция которой  на ось x задана в таблице.
на ось x задана в таблице.
Определить. Считая груз материальной точкой и зная расстояние АВ=l или время t1 движения груза от точки А до точки В, найти закон движения груза на участке ВС, т.е. x=f(t), где x=BD.
Указания. Задача решается в два этапа:
- сначала следует составить уравнение движения точки (груза) на участке АВ, с учетом начальных условий проинтегрировать уравнение методом разделения переменных; затем, зная время движения груза на участке АВ или длину этого участка, определить скорость груза в точке В. Эта скорость будет начальной для движения груза на участке ВС;
- составить и проинтегрировать дифференциальное уравнение движения груза на участке ВС с учетом начальных условий, ведя отсчет времени от момента, когда груз находится в точке В, и принимая в этот момент t=0; при интегрировании уравнения движения на участке АВ в случае, когда задана длина l участка, целесообразно перейти к переменному x, учитывая, что  .
.
Таблица Д-1
| Номер условия | m, кг | V0, м/с | Q, Н | R, H | l, м | t1, c | Fx, H |
| 0, 4v | - | 2, 5 | 2sin(4t) | ||||
| 2, 4 | 0, 8v2 | 1, 5 | - | 6t | |||
| 4, 5 | 0, 5v | - | 3sin(2t) | ||||
| 0, 6v2 | - | -3cos(2t) | |||||
| 1, 6 | 0, 4v | - | 4cos(4t) | ||||
| 0, 5v2 | - | -6sin(2t) | |||||
| 1, 8 | 0, 3v | - | 9t2 | ||||
| 0, 8v2 | 2, 5 | - | -8cos(4t) | ||||
| 0, 5v | - | 2cos(2t) | |||||
| 4, 8 | 0, 2v2 | - | -6sin(4t) |
5.2.1. Пример Д -1
На наклонном участке АВ трубы на груз D массой m действует сила тяжести, постоянная сила 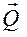 и сила сопротивления
и сила сопротивления 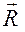 (рис. Д -1). Движение точки от точки А при v0 = 22 м/с до точки В происходит в течение t с.
(рис. Д -1). Движение точки от точки А при v0 = 22 м/с до точки В происходит в течение t с.
На горизонтальном участке ВС на груз кроме силы тяжести действует сила трения  и переменная сила
и переменная сила 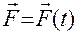 .
.
Дано: m =3 кг; v0= 22 м/c; Q = 9 H; R =μ v(H); μ =0, 5 кг/c; t= 3c; F=4sin(2t); α =300.
Определить: закон движения груза на участке ВС.

Рис. Д-1
Решение
1. Рассмотрим движение груза на участке АВ, считая груз материальной точкой. Изобразим в произвольном положении груз и действующие на него силы:  ,
, 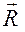 ,
, 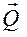 ,
,  . Проведем ось AZ и составим дифференциальное уравнение движения груза в проекциях на эту ось:
. Проведем ось AZ и составим дифференциальное уравнение движения груза в проекциях на эту ось:
 или
или 
или 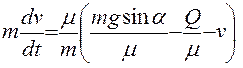 .
.
2. Введем обозначение:
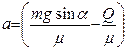 , откуда при заданных известных значениях получим а=12 м/с при g=10 м/с2.
, откуда при заданных известных значениях получим а=12 м/с при g=10 м/с2.
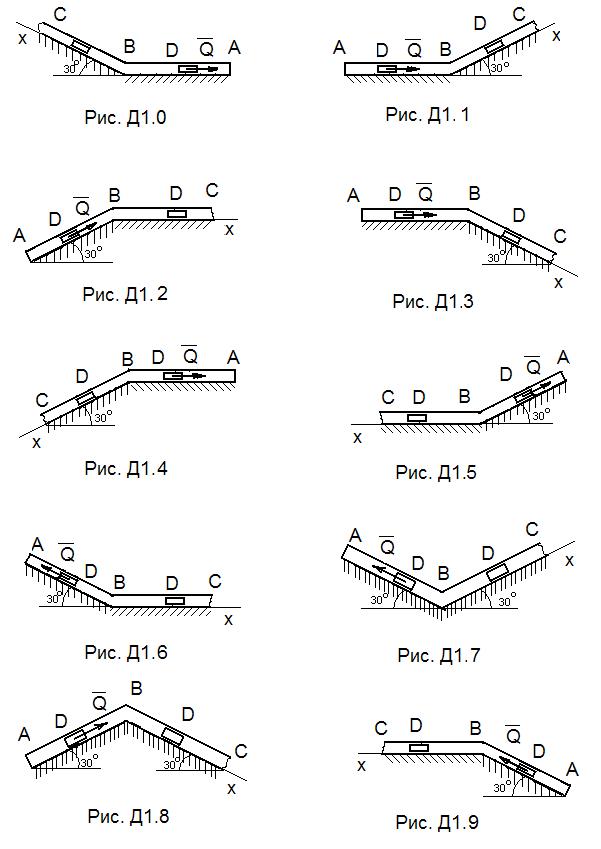
3. Разделив в уравнении переменные и взяв интегралы от обеих частей равенства, получим:
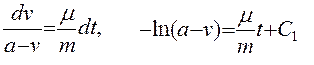 .
.
 | |||
 |
4. При известных начальных условиях: t=0, v0= 22 м/c получаем С1= -ln(a-22). Тогда уравнение примет вид:

5. После преобразования получим:
 или
или  .
.
6. Из п. 5 находим:
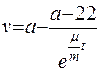
Полагая, что t=3 c, и заменив а, μ, m известными численными значениями, определяем скорость груза в точке В: vB= 18, 1 м/c.
7. Рассмотрим движение груза на участке ВС. Найденная скорость vB будет для движения груза на этом участке являться начальной скоростью (v0 = vB). Изобразим в произвольном положении груз и действующие на него силы:  ,
,  ,
, 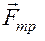 ,
,  .
.
8. Проведем из точки В оси BX и BY и составим дифференциальное уравнение движения груза в проекции на ось BX:
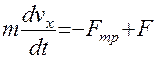 ,
,
где Fтр=fN.
9. Для определения N составим уравнение в проекции на ось BY. Так как в направлении BY нет движения, то  , поэтому 0=N-mg, откуда N=mg. Следовательно, Fтр=fmg. Учитывая, что F=4sin(2t), уравнение примет вид:
, поэтому 0=N-mg, откуда N=mg. Следовательно, Fтр=fmg. Учитывая, что F=4sin(2t), уравнение примет вид: 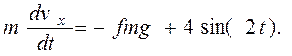
Разделив обе части равенства на m, получим:
 или
или 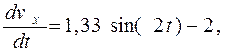
где 4/m=1, 33; fg =2 м/c2 при f=0, 2.
10. Умножив обе части уравнения на dt и проинтегрировав его, найдем
 .
.
11. При известных начальных условиях: t=0, v0 = vB = 18, 1 м/c - получим С2=18, 1 + 1, 33/2=18, 8.
12. Уравнение при найденной С2 примет вид:
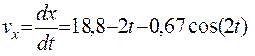 .
.
13. Умножая обе части на dt и снова интегрируя, получим:
 .
.
14. При t=0, x=0 С3=0, тогда закон движения груза окончательно будет представлен выражением:
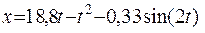 .
.
Ответ: 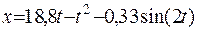
5.3. Теорема об изменении кинетической энергии материальной системы
Изменение кинетической энергии материальной системы на ее конечном перемещении равно сумме работ всех внешних и внутренних сил на этом перемещении:
 ,
,
где Т0 – начальное значение кинетической энергии системы.
5.3.1. Формулы для подсчёта кинетической энергии твердого тела в различных видах его движения
5.3.1.1. Тело движется поступательно
Скорости всех точек твердого тела одинаковы и равны скорости центра масс тела, поэтому:
 ,
,
где М – масса твердого тела, кг; Vc – скорость центра масс тела, м/с.
5.3.1.2. Тело вращается вокруг неподвижной оси
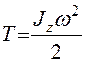 ,
,
где Jz – момент инерции тела относительно оси вращения тела, кг·м2; 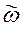 – угловая скорость вращения тела, 1/c.
– угловая скорость вращения тела, 1/c.
5.3.1.3. Тело совершает плоское движение
Плоское движение может быть рассмотрено как сумма поступательного движения тела со скоростью центра масс и вращательного движения тела вокруг оси Сz', перпендикулярной присоединенной плоскости и проходящей через центр масс тела, поэтому:
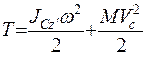 ,
,
где JСz' – момент инерции тела относительно оси вращения Сz', кг·м2; 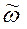 - угловая скорость вращения тела, 1/c; М – масса твердого тела, кг; Vc – скорость центра масс тела, м/с.
- угловая скорость вращения тела, 1/c; М – масса твердого тела, кг; Vc – скорость центра масс тела, м/с.
5.3.1.4. Тело вращается вокруг неподвижной точки
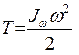 ,
,
где Jω – момент инерции тела относительно мгновенной оси скоростей, кг·м2.
Примечание: 1. Момент инерции цилиндра:  2. Момент инерции ступенчатого шкива:
2. Момент инерции ступенчатого шкива:  3. Момент инерции блока, масса которого равномерно распределена по ободу:
3. Момент инерции блока, масса которого равномерно распределена по ободу: 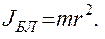
5.3.2. Примеры вычисления работы сил
1. Сумма работ внутренних сил системы в общем случае отлична от нуля.
2. Если материальная система представляет собой абсолютно твердое тело, то сумма работ внутренних сил равна нулю.
3. Работа любой силы равна нулю, если сила приложена в неподвижной точке, скорость которой равна нулю в данный момент времени.
4. Работа внутренних сил натяжений гибких нерастяжимых тросов, канатов и т.п. равна нулю.
5. Работа силы тяжести равна произведению веса материальной системы на вертикальное перемещение центра масс, взятому со знаком «плюс», если центр масс опускается, и со знаком «минус», если центр масс поднимается: А=± Mghc, где М – масса материальной системы, кг; hc – вертикальное перемещение центра масс, м; g – ускорение свободного падения, м/с2.
6. Работа силы, приложенной к вращающемуся вокруг оси абсолютно твердому телу, равна: А=± MП(φ -φ 0), где MП - момент пары сил, приложенной к телу, Нм; φ -φ 0 – значение конечного угла поворота тела.
7. Работа силы трения: А= - Fтр·S, где S - перемещение, м. Работа силы трения всегда отрицательна.
8. Работа сил упругости пружины: А=0, 5с∙ (λ 20 - λ 21), где с - коэффициент жесткости пружины; λ - удлинение пружины, м. Работа положительна при λ 0> λ 1 и отрицательна при λ 0< λ 1.
5.3.3. Д -2. Применение теоремы об изменении кинетической энергии к изучению движения механической системы
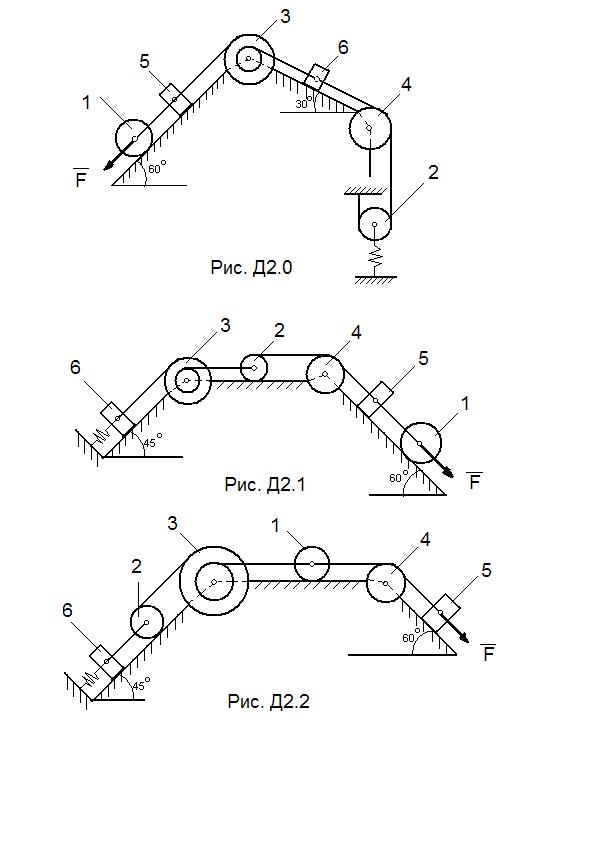
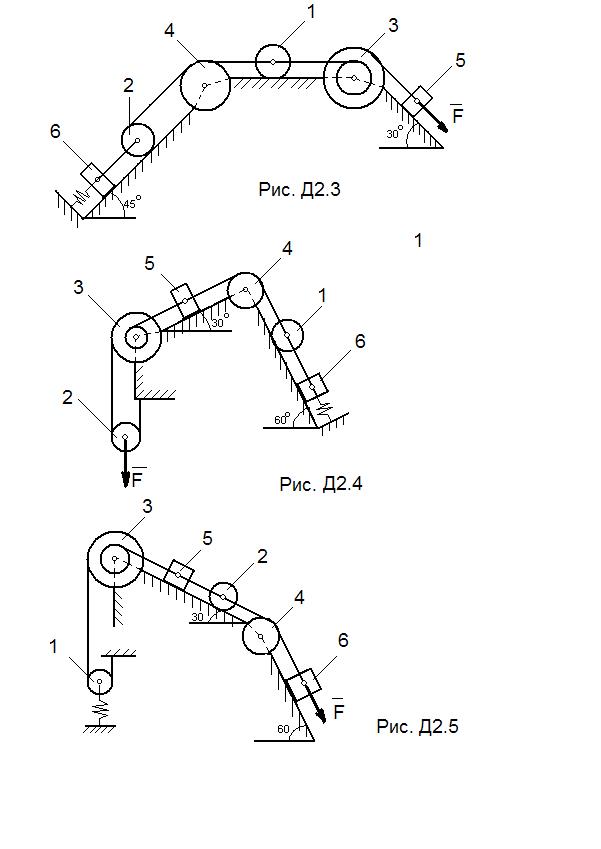
Дано. Механическая система состоит из катков 1 и 2 (или катка и подвижного блока), ступенчатого шкива 3 с радиусами ступеней R3= 0, 3 м, r3 = 0, 1 м и радиусом инерции относительно оси вращения ρ 3 = 0, 2 м, блока 4 радиуса R4= 0, 2 м и грузов 5 и 6 (рис. Д 2.0 – Д 2.9, табл. Д-2); тела 1 и 2 считать сплошными однородными цилиндрами, а массу блока 4 – равномерно распределенной по ободу. Коэффициент трения грузов о плоскость f=0, 1. Тела системы соединены друг с другом нитями, перекинутыми через блоки и намотанными на шкив 3 (или на шкив и каток); участки нитей параллельны соответствующим плоскостям. К одному из тел прикреплена пружина с коэффициентом жесткости с.
Под действием силы F=f(s), зависящей от перемещения s точки ее приложения, система приходит в движение из состояния покоя; деформация пружины в момент начала движения равна нулю. При движении на шкив 3 действует постоянный момент М сил сопротивления (от трения в подшипниках).
Все катки катятся по плоскостям без скольжения.
Если по заданию массы грузов 5 и 6 или массы катков 1 (рис. Д 2.0-2.4) и 2 (рис. Д 2.5-2.9) равны нулю, то на чертеже их можно не изображать.
Определить: значение искомой величины в тот момент времени, когда перемещение s станет равным s1= 0, 2 м. Искомая величина указана в столбце «Найти» таблицы Д 2, где обозначено: ω 3 – угловая скорость тела 3; ε 4 – угловое ускорение тела 4; v5 – скорость тела 5; ас2- ускорение центра масс тела 2 и т.п.
Указания. При решении задачи учесть, что кинетическая энергия системы равна сумме кинетических энергий всех входящих в систему тел; эту энергию следует выразить через ту скорость (линейную или угловую), которую в задаче надо определить. При вычислении энергии для установления зависимости между скоростями точек тела, движущегося плоскопараллельно, или между его угловой скоростью и скоростью центра масс воспользоваться мгновенным центром скоростей. При вычислении работы необходимо все перемещения выразить через заданное перемещение s1, учитывая при этом, что зависимость между перемещениями здесь будет такой же, как между соответствующими скоростями.
5.3.4. Пример Д -2
Механическая система состоит из грузов 1 и 2, ступенчатого шкива 3 с радиусами ступеней R3 и r3, радиусом инерции ρ 3 относительно оси вращения, блока 4 радиуса R4 и подвижного блока 5 (коэффициент трения грузов о плоскость равен f).Тела системы соединены нитями, намотанными на шкив 3.
К центру блока 5 прикреплена пружина с коэффициентом жесткости с; ее начальная деформация равна нулю.
Система приходит в движение из состояния покоя под действием силы F=f(s), зависящей от перемещения s точки ее приложения. На шкив 3 при движении действует постоянный момент М сил сопротивления.
Таблица Д-2
| Номер условия | m1, кг | m2, кг | m 3, кг | m 4, кг | m 5, кг | m 6, кг | c, Н/м | М, Нм | F=f(s), H | Найти |
| 1, 2 | 80(3+4s) | vc1 | ||||||||
| 0, 6 | 20(6+5s) | a6 | ||||||||
| 1, 8 | 60(4+s) | ω 4 | ||||||||
| 0, 3 | 40(3+8s) | ε 3 | ||||||||
| 1, 5 | 50(5+2s) | v6 | ||||||||
| 0, 9 | 30(4+3s) | ac1 | ||||||||
| 2, 4 | 60(2+5s) | v5 | ||||||||
| 0, 3 | 80(1+4s) | ε 4 | ||||||||
| 1, 2 | 20(8+3s) | ω 3 | ||||||||
| 0, 6 | 40(3+2s) | ac2 |
Дано: m1=0 кг, m2=5 кг, m3=6 кг, m4=0 кг, m5=4 кг, R3=0, 3 м, r3= 0, 1 м, ρ 3=0, 2 м, f=0, 1, с=240 Н/м, М=0, 6 Нм, F=80(3+2S)H, s1=0, 2 м.
Определить: vc5 в тот момент, когда s= s1.
Решение
1.Рассмотрим движение неизменяемой механической системы, состоящей из весомых тел 2, 3, 5 и невесомых тел 1 и 4, соединенных нитями. Изобразим действующие на систему внешние силы: активные F, Fупр, Р2, Р3, Р5, Fтр2, момент сопротивления М, натяжение нити S5 и реакции связей N2 , N3, N4 .
2. Для определения vc5 воспользуемся теоремой об изменении кинетической энергии:  , где
, где 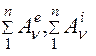 – соответственно, сумма работ внешних и внутренних сил системы.
– соответственно, сумма работ внешних и внутренних сил системы.
Для рассматриваемой системы, состоящей из абсолютно твердых тел, соединенных нерастяжимыми нитями, работа внутренних сил равна нулю.
В начальном положении все элементы механизма находились в покое, скорости всех тел были равны нулю, поэтому Т0=0.
3. Кинетическая энергия системы равна сумме энергий всех тел системы:
Т= Т2+ Т3+ Т5.
4. Выполним кинематический анализ:
- тело 2 движется поступательно;
- тело 3 вращается вокруг неподвижной оси;
- тело 5 участвует в плоскопараллельном движении.
Исходя из этого, кинетическая энергия системы может быть представлена выражением:
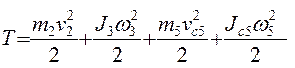 .
.

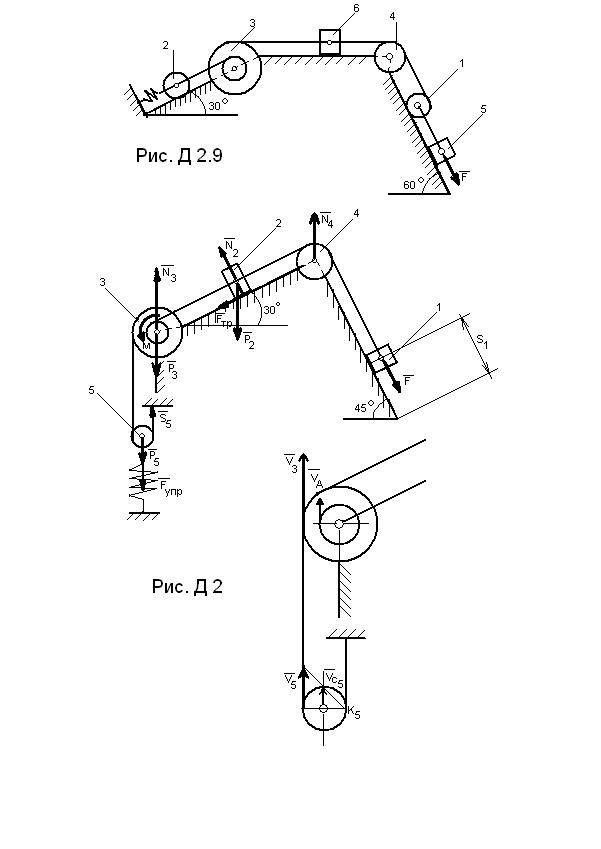
5. Кинетическая энергия Т, которую получила система после того, как груз переместился вдоль наклонной плоскости на расстояние s1, зависит от искомой скорости vc5. Поэтому все скорости, входящие в выражение кинетической энергии данной механической системы, выразим через скорость vc5.
6. Поскольку грузы 1 и 2 связаны нерастяжимой нитью, то их скорости равны. В свою очередь эта нерастяжимая нить перекинута через малый обод шкива 3, следовательно: v1= v2= vА, где vА – любая точка обода радиуса r3 шкива 3.
7. Линейные скорости шкива 2 и блока 5 зависят от одной угловой скорости ω 3: v2= ω 3r3, v5= ω 3R3.
8. Поскольку точка К5 является мгновенным центром скоростей для блока 5 (он как бы «катится» по участку нити К5L), то v5=2vc5. Тогда:
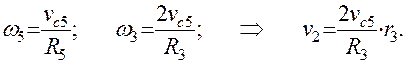
9. Осевые моменты инерции подвижного блока 5 и ступенчатого шкива 3 определяется выражениями:

10. Выполнив подстановку всех приведенных выше значений в выражение кинетической энергии для заданной механической системы, получим:
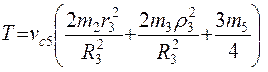 .
.
11. Находим работу всех действующих внешних сил при перемещении, которое будет иметь система, когда груз 1 пройдет путь s1=0, 2 м. Введем следующие обозначения: s2 – перемещение груза 2 (s2=s1); φ 3 – угол поворота шкива 3; h5 – перемещение центра масс блока 5; λ 0, λ 1 –начальное и конечное удлинение пружины.
Сумма работ всех внешних сил равна:
 , где
, где
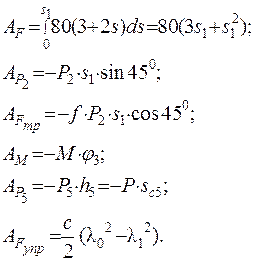
Работы остальных сил равны нулю:
- точка К5 – мгновенный центр скоростей, поэтому работа силы натяжения
- нити S5 равна нулю;
- реакция опоры N2 перпендикулярна перемещению груза 2, а поэтому работы не совершает;
- реакции N3, N4, приложенные в неподвижных точках, не совершают работы.
По условию задачи λ 0=0, тогда λ 1 = sc5 – перемещение конца пружины. Выразим величины sc5 и φ 3 через заданное перемещение s1. Зависимость между перемещениями такая же, как между соответствующими им скоростями:

12. Поскольку v5=v3=ω 3R3 и vc5=0, 5v5, то vc5=0, 5ω 3R3. Следовательно, λ 1 = sc5=0, 5φ 3R3=0, 5(s1R3)/r3.
13. При найденных значениях φ 3 и λ 1 получим выражение для подсчета суммы работ всех внешних сил, действующих на механическую систему:
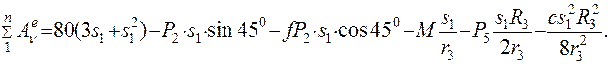
14. Кинетическую энергию приравниваем к работе:
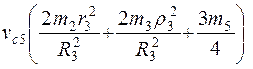 =
=
= 
Подставив в полученное выражение известные численные значения заданных величин, найдем искомую скорость vc5.
Ответ: vc5 = 2, 10 (м/c).
Литература
1. Аршинова, В.А. Конспект лекций по теоретической механике: учебное пособие / В.А. Аршинова, А.И.Зайцев. – Ярославль: ЯГТУ, 1998. – 176 с.: ил.
2. Голдобина Л.А. Теоретическая механика: контрольные задания и методические указания к выполнению курсовой работы для студентов специальности 311300 – «Механизация сельского хозяйства» дневной и заочной форм обучения / Л.А. Голдобина, К.А.Зиновьев. – Ярославль: ЯГСХА, 2000. – 64 с.: ил.
3. Первов, А.А. Методические указания к решению задач по теоретической механике для студентов механических и технологических специальностей. – Ярославль: ЯПИ, 1984. – 25 с.: ил.
4. Теоретическая механика: методические указания и контрольные задания для студентов-заочников машиностроительных, строительных, транспортных, приборостроительных высших учебных заведений/ Л.И. Котова, Р.И. Надеева, С.М. Тарг и др.; под ред. С.М. Тарга. – 4-е изд. – М.: Высш. шк., 1989. – 111 с.: ил.
5. Теоретическая механика: методические указания и контрольные задания для студентов-заочников машиностроительных, строительных, транспортных, приборостроительных высших учебных заведений/ Л.И. Котова, Р.И. Надеева, С.М. Тарг и др.; под ред. С.М. Тарга. – 4-е изд. – М.: Высш. шк., 1978. – 88 с.: ил.
Приложение А.1. Пример оформления содержания работы
Содержание
Стр.
Глава 1. Статика………………………………………………………………
1.1.С-1. Произвольная плоская система сил. Определение реакций
связей сплошной конструкции ………………….………………………
1.2.С -2. Произвольная пространственная система сил. Определение
реакций связей.……………………………………………………………….
Глава 2. Кинематика…………………………………………………………..
2.1. К -1. Кинематика точки. Определение скорости и ускорения точки
по заданным уравнениям ее движения………………………………………
2.2. К -2. Плоскопараллельное движение твердого тела. Определение
скоростей и ускорений точек многозвенного механизма………………….
2.3. К -3. Сложное движение точки. Определение абсолютной скорости
и абсолютного ускорения точки…………………………………………….
Глава 3. Динамика………………………………………………………………
3.1. Д -1. Динамика материальной точки. Интегрирование
дифференциальных уравнений движения материальной точки,
находящейся под действием постоянных сил………………………………
3.2. Д -2. Применение теоремы об изменении кинетической энергии
к изучению движения механической системы………………………………
Приложение А.2. Условные обозначения
| № п/п | Наименование величин | Обозначение |
| Вектор силы | 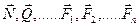
| |
| Модуль силы | N, Q, ….F1, F2, … Fn | |
| Проекции силы на координатные оси | XA, YA, ZA | |
| Векторный момент силы относительно точки | 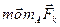
| |
| Скалярный момент силы относитнельно точки | 
| |
| Момент силы относительно оси | 
| |
| Относительные: скорость, ускорение | 
| |
| Переносные: скорость, ускорение | 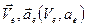
| |
| Угловая скорость | 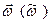
| |
| Угловое ускорение | 
| |
| Ускорение Кориолиса | 
|