
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Циклічних обчислювальних процесів
|
|
Розв’язання багатьох задач зводиться до виконання обчислень за тими самими математичними залежностями, але при різних значеннях величин, які у них входять. Такий обчислювальний процес має назву циклічного, а багаторазово повторювані ділянки цього процесу – циклів. Змінні, що змінюються при кожному новому виході на повторення, мають назву параметрів циклу. Змінна, значення якої обчислюється і зберігається в одній тій самій комірці пам'яті ЕОМ, зветься простою змінною. Змінна, що є елементом масиву, зветься змінною з індексом. При використанні простої перемінної параметром циклу є сама змінна. При використанні змінної із індексом параметром циклу є її індекс. В одному циклі можуть бути кілька параметрів.
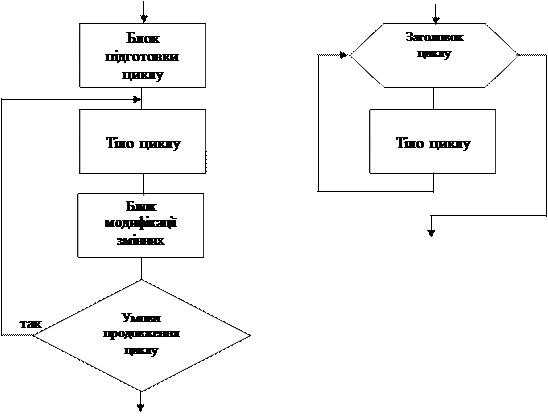
Алгоритм циклічної структури в загальному вигляді повинен містити:
- підготовку циклу - завдання початкових значень змінним циклу перед першим його виконанням;
- тіло циклу - дії, повторювані в циклі для різних значень параметрів циклу;
- зміну значень параметрів циклу перед кожним новим його повторенням;
- керування циклом - перевірку умови продовження (закінчення) циклу і перехід на початок тіла циклу, якщо виконується умова продовження циклу (або вихід з циклу після його закінчення).
Для організації циклічної структури можуть використовуватися або блоковий символ " розв’язання" у сукупності із символами " процес" (варіант А), або спеціальний блоковий символ " модифікація" (варіант В). Два варіанти організації циклічної структури наведено на рис. 1.
В)
 | |||
|
Розрізняють регулярні або арифметичні цикли (з відомим числом повторень), умовою закінчення яких є досягнення параметром циклу свого кінцевого значення, і цикли ітераційні (з невідомим числом повторень). У таких циклах умова повторення або закінчення циклу задається по деякому проміжному або остаточному результату, наприклад, поки не буде досягнута необхідна точність обчислень.
Регулярні цикли називають також циклами з лічильником. Число повторень тіла циклу в цьому випадку підраховується за допомогою введення спеціальної змінної – лічильника, для якої відомі початкове, кінцеве значення та крок її зміни. Управління циклом здійснюється на підставі порівняння поточного значення лічильника із заданим порогом. Число повторень тіла циклу визначається за формулою:
N = ](хк - хн)/h[ + 1,
де хк - кінцеве значення параметра циклу;
хн - початкове значення параметра циклу;
h - крок зміни параметра циклу.
Поточне значення параметра циклу обчислюється за формулою:
х = хн + (k - 1)h,
де k змінюється від 1 до N.
При реалізації циклічних обчислювальних процесів використовуються рекурсивні вираження, що описують будь-який член послідовності чисел.
Наприклад, формула х = х + 1, у якій реалізована рекурсія, означає, що до вмісту комірки пам'яті з іменем х додається 1 і результат записується в х. Така формула зветься рекурентною і зв'язує між собою значення змінної х, що обчислюються послідовно. Вхідними даними для кожного наступного кроку є результати попереднього.
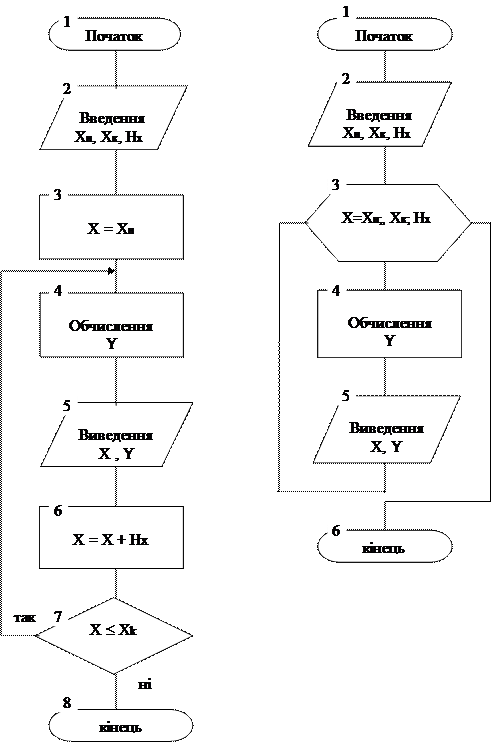
Приклад 1. Скласти алгоритм обчислення виразу y = x - sin(x), де x змінюється від xн = 0 до xк = 5 із кроком h = 0, 15.
Схема алгоритму задачі (рис. 2) являє собою простий циклічний обчислювальний процес із неявно заданим числом повторень. Поняття рекурсії використовується також при обчисленні суми або добутку кінцевої кількості чисел. При цьому необхідно виконати наступні дії:
- сформувати вхідні дані;
- визначити початковий стан комірки, в якій провадиться накопичення суми або добутку;
- організувати цикл накопичення суми чи добутку;
- вивести результат.
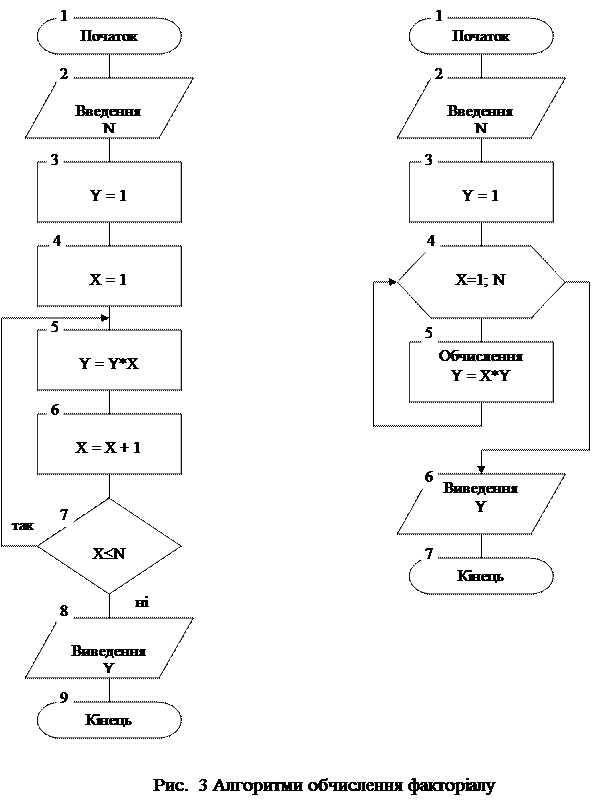
Приклад 2. Скласти алгоритм обчислення значення факторіалу Y = N! (добутку чисел натурального ряду від 1 до N: 2! = 1*2; 3! = 1*2*3; 4! =1*2*3*4; N! =1*2*3*...*N). Два варіанти схеми алгоритму обчислення факторіалу наведено на рис. 3.
 |
В)
А)
|
В)
А)
3 Контрольні питання
3.1 Визначити поняття “циклічний обчислювальний процес”.
3.2 Визначити поняття “цикл”.
3.3 Визначити поняття “параметр циклу”.
3.4 Який склад алгоритму циклічної структури.
3.5 Які різновиди циклічних алгоритмів?
3.6 Які дії необхідно виконати для організації арифметичного циклу?
3.7 Визначити поняття “рекурсія”.
3.8 Наведіть приклади задач, які описуються циклічними алгоритмами.