Проектування алгоритмів сортування

Існує N значень, які потрібно упорядкувати за зростанням (або спаданням), якщо мова йде про числові значення, або за алфавітом, якщо мова йде про ланцюжки символів.

Методи сортування дуже важливі в теоретичному відношенні і мають велике поширення як у наукових задачах, так і в задачах управління. Вони породили величезне число досліджень. На такому прикладі як сортування, який легко формулюється, можна порівнювати різноманітні алгоритми, досліджувати їхню складність і поведінку в залежності від числа і форми даних. У більшості машин існують стандартні програми сортування і користувач урятований від необхідності писати свою власну програму.

Для сортування всі дані потрібно ввести в машину. Припустимо, що потрібно впорядкувати за зростанням числові дані, які містяться в пам’яті в масиві Т розміром N. Існує багато різноманітних алгоритмів сортування, що дозволяють вирішити цю задачу.

" Кулькове" сортування. Назва походить від образної інтерпретації, при якій у процесі виконання алгоритму більш " легкі" елементи потрохи підіймаються на " поверхню".

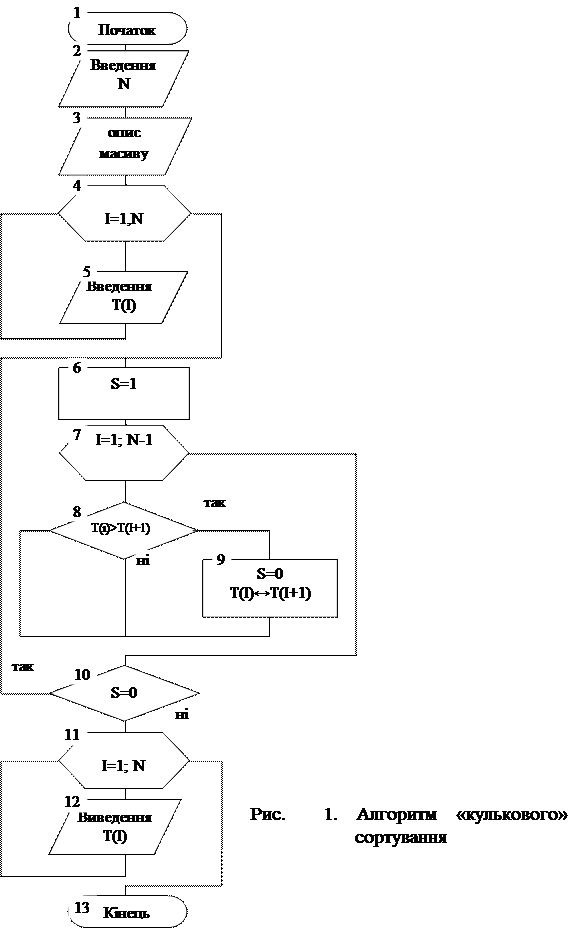
Алгоритм (рис.1) " кулькового" сортування складається з послідовних проходів від початку до кінця масиву введених даних Т і обміну сусідніх елементів з інверсією.

Порівнюють пари значень Т(I) і Т(I+1) при I в інтервалі від 1 до N-1; якщо Т(I)> T(I+1), то значення переставляються місцями.

Сортування зупиняється, коли немає чого переставляти; у цьому випадку сортування масиву закінчується.

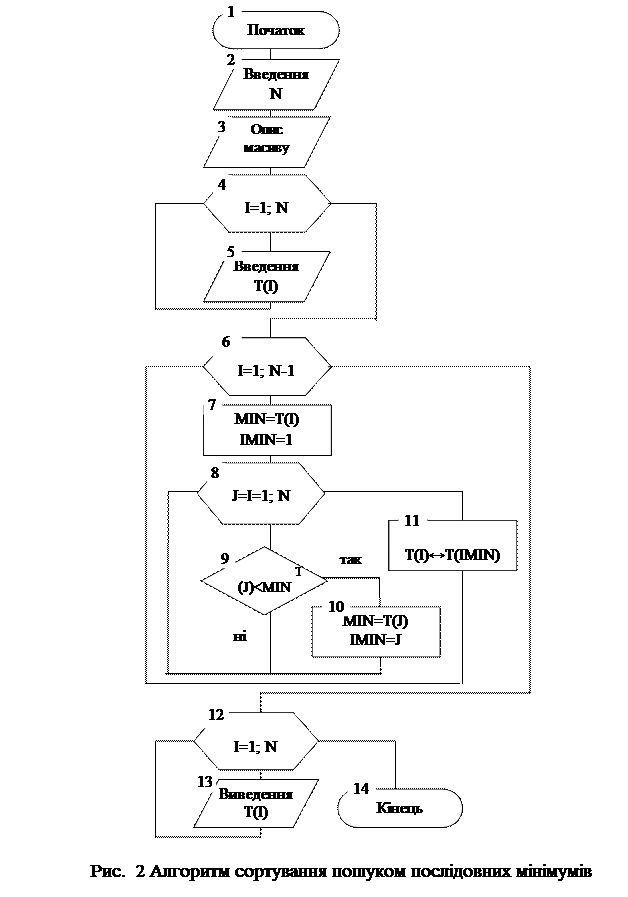
Сортування пошуком послідовних мінімумів. При першому проході шукається мінімальне значення масиву Т, що потім змінюється місцями з першим елементом T(1), потім пошук продовжується на N-1 елементах, що залишилися, шукається другий мінімум, що змінюється з елементом Т(2) і т.д. Алгоритм сортування пошуком послідовних мінімумів наведено на рис.2.

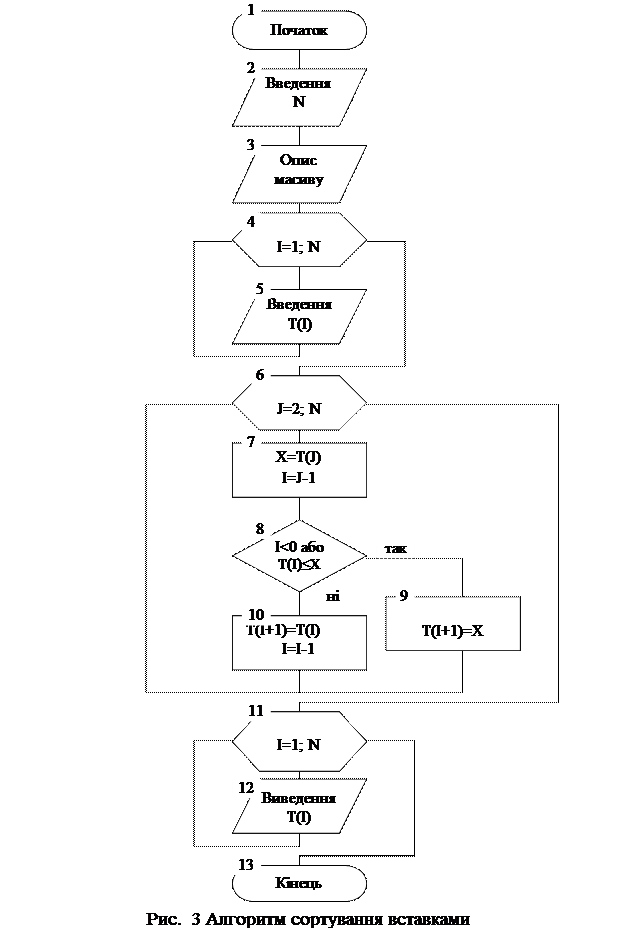
Сортування методом вставки. Щоб відсортувати масив Т, достатньо вставити T(J) у J-1 вже сортованих перших елементів, при цьому J змінюється від 2 до N. Алгоритм сортування методом вставки наведено на рис.3.

Швидке сортування SHELL-SORT є вдосконаленим методом вставки. Ідея, що покладена в основу цього метода така, що дані попередньо сортуються у блоках, а потім кількість блоків зменшується до тих пір, поки усі данні не будуть в одному блоці. Тим самим значно зменшується кількість обмінів. На операції обмінів у програмі для сортування даних витрачається багато машинного часу. Швидке сортуванняQUICKSORT є одним із найшвидших методів сортування. Серед N значень, які треба відсортувати, обирається значення, яке називають провідним елементом. Цей вибір може проводитися випадковим чином. Потім у початок масиву ставляться усі елементи, менші за провідний, а у кінець –усі інші. На кожній з отриманих послідовностей ця операція повторюється до тих пір, доки не одержані послідовності, які мають один або два елементи. Таким чином масив відсортований. Ефективність цього методу є високою лише у тому випадку, коли вибрані провідні елементи розділяють кожну послідовність на послідовності приблизно однієї довжини.

Розберемо приклад. Дано деяку послідовність чисел:

4 3 7 6 9 1 0 2 5

Виберемо перше (4), останнє (5) та число (9), яке знаходиться посередині. Середнім числом D є 5, і по ньому дана послідовність ділиться на 2 підгрупи. Для цього число D переставляється на праве провідне місце (у цьому прикладі воно вже там стоїть). Тепер, починаючи з провідного лівого, шукається число більше за 5, а з правого – число менше за 5, і ці числа переставляються місцями. У даному випадку це числа 2 та 7.

4 3 2 8 9 1 0 7 5

Пошук продовжується до тих пір, доки не зупиниться на числі, котре не вдасться переставити з жодним іншим числом. Таким чином послідовність має вигляд:

4 3 2 0 1 9 8 7 5

Потім це число (у даному випадку 9) зміняється з числом, що стоїть у правому кінці (у даному випадку числом 5). Це дає:

4 3 2 0 1 5 8 7 9

Тепер число 5 стоїть на тому місці, на якому воно буде стояти після закінчення сортування. Таким самим чином сортуються обидві підгрупи (4 3 2 0 1) і (8 7 9), доки в кожній з них не залишиться по одному числу.

3 Контрольні питання

3.1 Зазначте області застосування сортування.

3.2 Сутність методу " кулькового" сортування.

3.3 Сутність сортування методом послідовних мінімумів.

3.4 Сутність сортування методом вставки.

3.5 Методи швидкого сортування.