Навчальний матеріал. Розрізняють регулярні, або арифметичні цикли (з відомим числом повторень), умовою закінчення яких є досягнення параметром циклу свого кінцевого значення

Розрізняють регулярні, або арифметичні цикли (з відомим числом повторень), умовою закінчення яких є досягнення параметром циклу свого кінцевого значення, і цикли ітераційні (з невідомим числом повторень). У таких циклах умова повторення або закінчення циклу задається по деякому проміжному або остаточному результату, наприклад, поки не буде досягнута необхідна точність обчислень.

При реалізації ітераційних обчислювальних процесів в алгоритмах повинно забезпечуватися обов'язкове виконання умови виходу з циклу, тобто збіжність ітераційного процесу.

Прикладом ітераційних обчислювальних процесів є обчислення нескінченних числових рядів. При цьому для практичних розрахунків обмежуються обчисленням деякого числа елементів, виходячи з вимог заданої точності обчислення заданої суми членів ряду S.

Числовий ряд, що сходиться – це ряд, кожний наступний член якого має значення, яке менше значення попереднього члена ряду. У цьому випадку сума членів ряду є скінченою величиною. Обчислення суми членів ряду припиняється на черговому члені ряду, значення якого менше заданої точності.

Ітераційні алгоритми для обчислення сум нескінченних рядів будуються в наступному порядку:

- вводяться необхідні вхідні дані;

- задаються початкове значення суми і значення допоміжних змінних (за необхідності);

- обчислюється значення поточного члена ряду;

- виконується порівняння значення поточного члена ряду з заданою точністю ;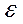

- якщо значення члена ряду не менше заданої точності 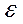, то він додається до накопиченої суми і змінюються значення допоміжних змінних, після чого здійснюється перехід на обчислення чергового члена ряду і цикл повторюється;

- якщо значення поточного члена ряду менше заданої точності 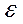, то здійснюється вихід з циклу і виводиться отриманий результат.

В алгоритмах, що реалізують ітераційні обчислювальні процеси, неприпустимим є використання блоків модифікації, тому що відсутня керуюча змінна – параметр циклу.

Приклад: Скласти алгоритм для обчислення суми збіжного ряду з точністю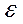

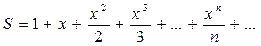
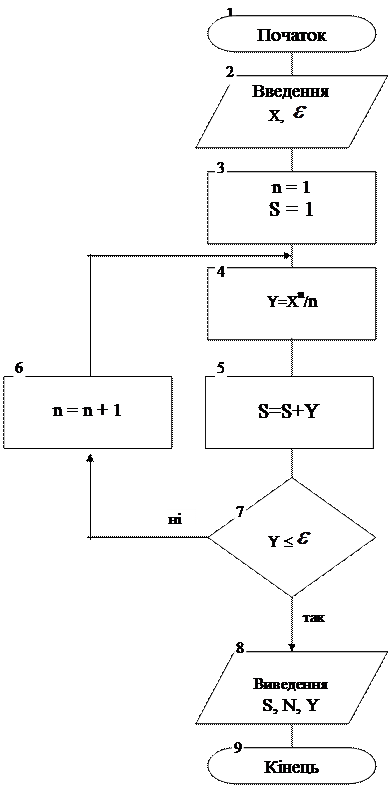
На схемі алгоритму (рис. 1) у блоці 3 задаються вхідні значення номера n - го члена ряду, що обчислюється, і початкове значення суми членів ряду S. У даному випадку n = 1 і S = 1, тобто обчислення починаються з другого члена ряду, тому що перший член ряду дорівнює одиниці і не обчислюється за загальною формулою члена ряду.

Накопичення суми виконується в блоці 5 за допомогою рекурсивної залежності:

S = S + Y,

де Y – значення чергового обчисленого члену ряду.

	Рис. 1 Алгоритм обчислення суми нескінченного ряду

3 Контрольні питання

3.1 Що означає ітераційний циклічний процес?

3.2 Які умови збігу методу ітерацій?

3.3 Вкажіть порядок побудови ітераційного алгоритму.

3.4 Як організується вихід з циклу в ітераційному алгоритмі?

3.5 Яким чином в ітераційних циклах використовуються рекурсивні відношення?

3.6 Чому при програмуванні ітераційних процесів не використовуються індексні змінні для позначення послідовних наближень?

3.7 Для яких задач застосовують ітераційні цикли?