
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Проектування алгоритмів обробки одновимірних масивів
|
|
Масив - це впорядкований набір однорідних елементів, що мають ім’я, для зберігання яких наділяється послідовно розташоване поле пам'яті. Масив характеризується ідентифікатором (ім'я), числом вимірів (індекси) і числом змінних у кожному вимірі (верхня межа кожного індексу). Існують одновимірні масиви (вектори, лінійні таблиці), двовимірні масиви (матриці, прямокутні таблиці), а також багатовимірні масиви.
Введення - виведення елементів масиву виконується поелементно. Можливі два способи.
Спосіб 1. Безпосереднє введення-виведення елементів масиву, яке позначається на блок-схемі алгоритму при введенні значень елементів блоками “введення” або “процес” та при виведенні блоком “виведення”.
Такий спосіб доцільно застосовувати, коли масиви мають малі розміри.
Спосіб 2. При великих розмірах масивів, що оброблюються, оператори введення-виведення розміщують усередині циклічної ділянки програми і при кожному виконанні циклу здійснюється введення-виведення одного елемента.
При складанні циклічних програм обробки масивів доцільно сполучати операції введення і безпосередньо обробки масивів, що дозволяє в ряді випадків скоротити обсяг програми.
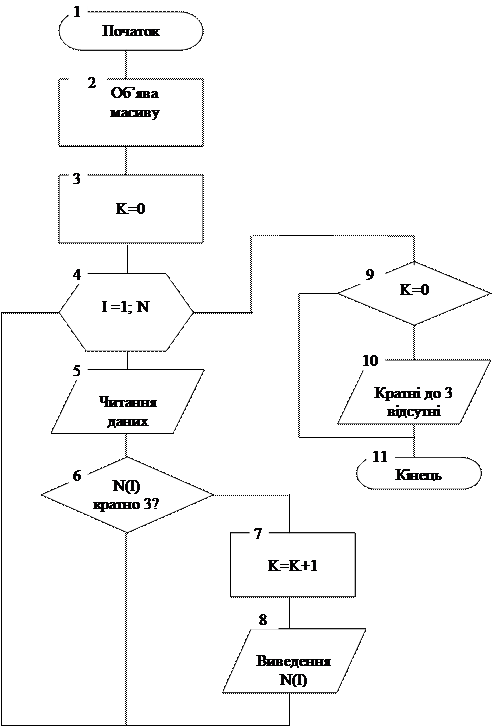
Приклад 1: Вивести на друк елементи цілочисельного масиву N=[n1, n2, n3,..., n50], які кратні трьом. Сполучимо операції введення поточного значення елемента масиву і його опрацювання.
 | |||
|
Рис. 1 Алгоритм визначення елементів масиву, кратних 3.
Якщо ж потрібно запам'ятати всі значення результатів у пам'яті, то необхідно виділити масив для результатів, і обчислити результат як змінну з індексом.
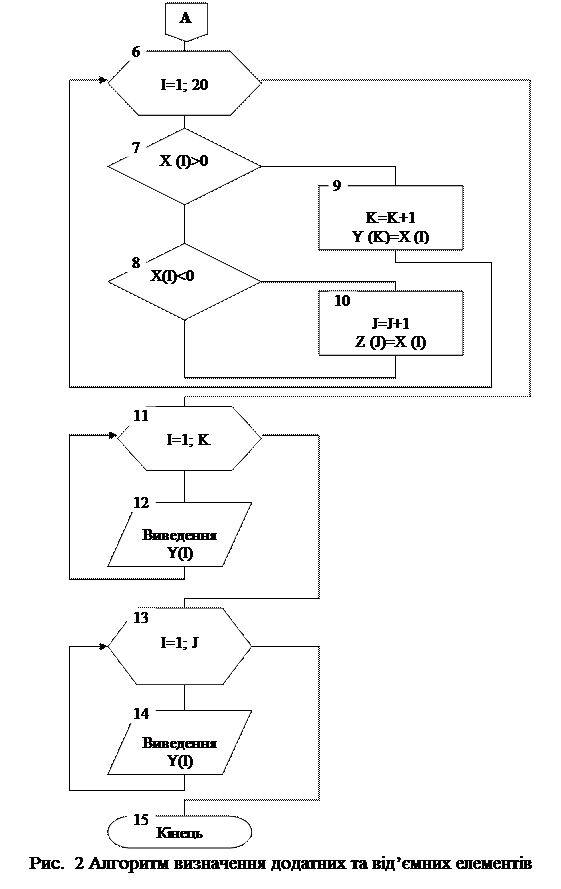
Приклад 2: Переписати підряд у масив Y додатні елементи масиву (x1, x2, x3,..., x20), а в масив Z - від’ємні.
 Особливість рішення полягає в тому, що елементи, які записуються в масиви Z і Y, повинні розташовуватися підряд без пропусків. Це призведе до того, що індекси змінних yk та zj набудуть значень, відмінні від значень індексів змінної xi. Тому в циклі необхідно змінювати значення k та j кожний раз перед записом відповідного елементу x, тобто необхідно використати спосіб організації циклу з кількома параметрами, які одночасно змінюються (рис. 2.).
Особливість рішення полягає в тому, що елементи, які записуються в масиви Z і Y, повинні розташовуватися підряд без пропусків. Це призведе до того, що індекси змінних yk та zj набудуть значень, відмінні від значень індексів змінної xi. Тому в циклі необхідно змінювати значення k та j кожний раз перед записом відповідного елементу x, тобто необхідно використати спосіб організації циклу з кількома параметрами, які одночасно змінюються (рис. 2.).
Знаходження суми 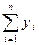 зводиться до її накопичення у вигляді значення змінної в циклі, в який вводяться відповідні додатки. При цьому наступний додаток yi додається до суми попередніх додатків zi-1, тобто в циклі послідовно обчислюються всі проміжні суми:
зводиться до її накопичення у вигляді значення змінної в циклі, в який вводяться відповідні додатки. При цьому наступний додаток yi додається до суми попередніх додатків zi-1, тобто в циклі послідовно обчислюються всі проміжні суми:
z1 = z0 + y1 = y1
z2 = z1 + y2 = (y1) + y2
..............................
zi = zi-1 + yi = (y1 + y2)+yi
..............................
zn = zn-1 + yn
zn = 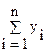
Обчислення добутку зводиться до його накопичення в циклі у вигляді значення змінної. Аналогічно накопиченню суми в циклі обчислюються послідовно всі проміжні добутки:
z1 = z0 * y1 = y1
z2 = z1* y2 = (y1) * y2
.............................
zi = zi-1 * yi = (y1 * y2)*yi
..............................
zn = zn-1 * y n
zn = 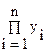
Якщо не потрібно зберігати у пам’яті комп’ютера додатки і проміжні добутки, вони представляються простими змінними; і тоді рекурентна формула для накопичення добутку має вигляд:
z = z * y.
де y - множник; z - проміжний добуток.
Перед циклом за початкове значення добутку, як правило, приймається одиниця: z0 = 1.
Приклад 3: Скласти алгоритм обчислення математичного сподівання mx випадкової величини x, використовуючи розрахункову формулу
mx = 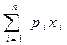
для початкових даних: n = 5; рi = {0.3; 0.25; 0.2; 0.1; 0.15};
xi = {90; 80; 120; 95; 110}.
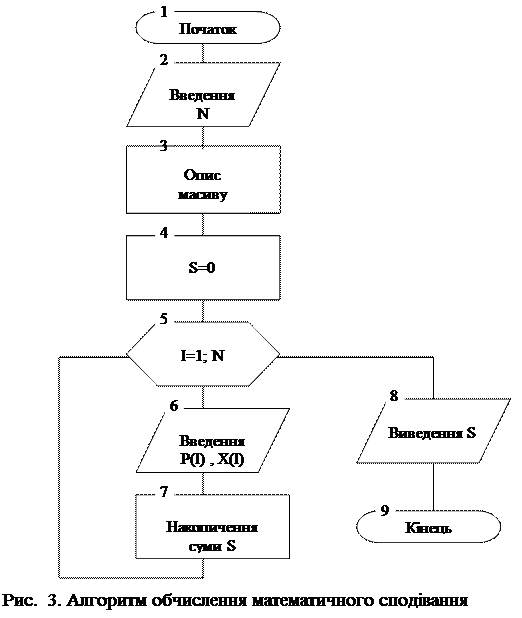 Початковими даними для обчислення є проста змінна N та два масиви: P і X. Результат обчислення збережемо у простій змінній S. Для накопичення суми організується цикл, параметром якого є індекс I, який змінюється від 1 до N. (рис.3.)
Початковими даними для обчислення є проста змінна N та два масиви: P і X. Результат обчислення збережемо у простій змінній S. Для накопичення суми організується цикл, параметром якого є індекс I, який змінюється від 1 до N. (рис.3.)
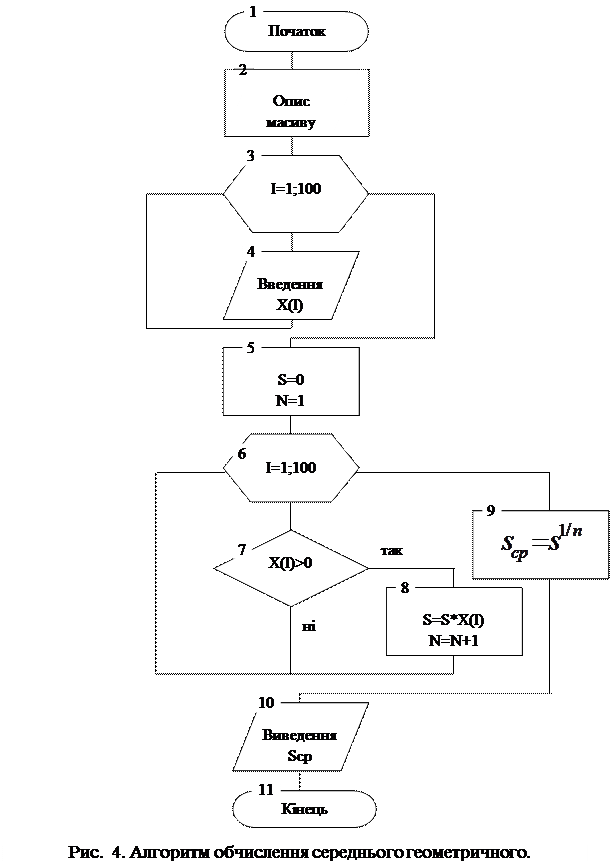 Приклад 4: Скласти алгоритм обчислення середнього геометричного додатних елементів масиву. Схема алгоритму наведена на рис.4.
Приклад 4: Скласти алгоритм обчислення середнього геометричного додатних елементів масиву. Схема алгоритму наведена на рис.4.
Знаходження найбільшого та (або) найменшого з множень значень виконується у циклі шляхом порівняння деякого поточного значення з найбільшим (найменшим) з усіх попередніх.
Якщо поточне значення більше від найбільшого (МАХ) з усіх попередніх, то МАХ присвоюється значення поточного. У протилежному випадку зберігається попереднє значення. Процес можна описати наступною залежністю:
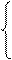 yi, якщо yi> ymax
yi, якщо yi> ymax
ymax =
ymax, якщо yi £ ymax
 Після закінчення циклу значення ymax буде найбільшим з усіх розглянутих значень yi.
Після закінчення циклу значення ymax буде найбільшим з усіх розглянутих значень yi.
Аналогічним чином знаходиться найменше (MIN) серед набору елементів, із використанням залежності:
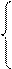 yi, якщо yi< ymin
yi, якщо yi< ymin
ymin =
ymin, якщо yi ³ ymin
При знаходженні найбільшого (МАХ) та (або) найменшого (MIN) елемента масиву за початкове значення найбільшого та найменшого у цьому випадку слід брати значення першого елемента масиву, а в циклі, пошук найбільшого та найменшого елементу виконувати, починаючи з другого елементу масиву.
Приклад 5: Скласти алгоритм знаходження найбільшого та найменшого елемента масиву (х1, х2, ….хk) та їх порядкових номерів.
Особливість пошуку полягає в тому, що необхідно знаходити номер найбільшого та найменшого елемента. Прийнявши за початкове значення і максимальний і мінімальний елемент, запам’ятаємо їх номери іmax = 1 і іmin= 1. У циклі при виконанні умов xi> xmax та хi< хmin присвоюють, відповідно, xmax=xі, іmax = і та хmin=хi , іmin = і (рис. 5.)

3 Контрольні питання
3.1 Дайте визначення масиву.
3.2 Які характеристики мають масиви?
3.3 Опишіть особливості алгоритмів введення і виведення елементів масиву.
3.4 Опишіть реалізацію накопичення суми і добутку скінченого числа елементів масиву.
3.5 Як організувати рахунок кількості елементів?
3.6 Як організувати процес формування нових масивів у процесі розв’язання задач?
3.7 Як організувати знаходження найбільшого і найменшого елементів масиву?
3.8 Як організувати процес упорядкування елементів масиву?
3.9 У чому особливість організації циклу при обробці масивів?