Рекуррентные байесовские алгоритмы

Линейный фильтра Калмана

Для линейных моделей динамической системы и измерений:

где

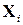- n-мерный вектор состояния системы,

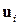- m-мерный вектор управления,

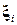- n-мерный вектор случайных возмущений,

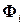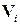, - матрицы размерностью nxn и nxm соответственно, зависящие в общем случае от номера i,

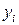- l-мерный вектор измерений,

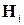- матрица lxn, элементы которой зависят от i,

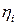- l-мерный вектор независимых ошибок измерений, распределенных по нормальному закону,

возможно применение линейной модификации фильтра Калмана, соотношения которого для прогноза и коррекции вектора состояния даны ниже. Соотношения прогноза случайного вектора состояния динамической системы:

,

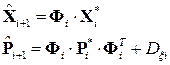где

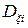- ковариационная матрица случайных возмущений в канале движения в момент времени i,

- апостериорная ковариационная матрица, характеризующая точность получаемых оценок, может быть получена независим от измерений, заранее.

Соотношения коррекции представлены ниже:

,

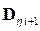- корреляционная матрица ошибок измерений.

Приведенные в данном разделе соотношения подходят для использования только в линейном случае моделей динамической системы и измерений, что встречается редко. Поэтому зачастую требуется решить задачу оптимальной фильтрации для нелинейных систем. Для этого существует квазилинейная модификация фильтра Калмана.

Квазилинейный фильтр Калмана

Квазилинейная модификация фильтра Калмана используется тогда, когда уравнения, описывающие рассматриваемую систему, не поддаются выделению линейного аналитического вида:

,

где

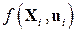- функция состояния,

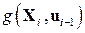- вектор-функция измерения.

В таких случаях нет возможности построить точную линейную модель и поэтому рассматриваемую систему линеаризуют.

Уравнения прогноза квазилинейного фильтра для линеаризованной системы:

,

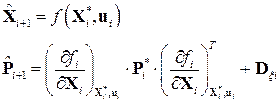Уравнения коррекции: