Комплексные системы измерения местоположения и скорости ЛА (КИМС).

К числу основных навигационных устройств обеспечивающих получение на борту ЛА информации об его местоположении и скорости относятся: ИНС, аэрометрический измеритель воздушной скорости в структуре СВС и радиотехнические измерители (ДИСС, РВ). Поэтому задача повышения точности и надежности определения местоположения и скорости ЛА может быть решена путем комплексирования:

1) ИНС и ДИСС для определения скорости;

2) ИНС, ДИСС и РВ для определения пространственного местоположения ЛА.

Учитывая различие спектральных характеристик ошибок ИНС, ДИСС и РВ можно ожидать выигрыша в точности определения местоположения и скорости в результате такого комплексирования.

Другим вариантом построения комплексной системы измерения местоположения и скорости является оптимальное комплексирование ДИСС и измерителя воздушной скорости, входящего в состав СВС. Возможность такого комплексирования обусловлена тем, что выходной сигнал ДИСС имеет широкополосный характер, а выходной сигнал измерителя воздушной скорости является низкочастотным случайным процессом.

Структурная схема и принцип построения радиоинерциальнодоплеровскй (РИД КИМС) системы измерения местоположения и скорости ЛА Ранее мы указывали, что КСН, в состав которых входит ИНС целесообразно строить по замкнутой схеме компенсации ошибок с целью коррекции накапливающихся ошибок ИНС. Однако в случаях небольшой продолжительности полета ЛА (в пределах часа) вполне можно использовать КИМС, построенную на основе бюолее простой разомкнутой схемы компенсации. Структурная схема КИМС в этом случае имеет следующий вид;

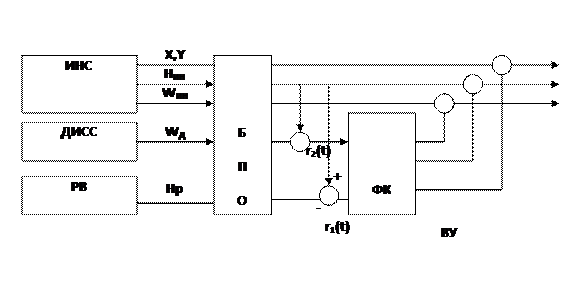
Рассмотрим основные элементы приведенные на структурной схеме КИМС. Для этого напомню ориентацию осей систем координат, в которых проводятся измерения комплексируемых устройств.

Выходной сигнал ИНС представляет собой измерения координат X, Y местоположения ЛА и его высоты Н_ИН в инерциальной системе координат, используемой для навигации ЛА

ДИСС измеряет составляющие вектора путевой скорости ЛА в направлении линий визирования бортовых антенн, не совпадающих с осями инерциальной системы координат.

РВ измеряет высоту относительно поверхности Земли с учетом рельефа местности. Это значение высоты в общем случае отличается от инерциальной высоты поступающей с выхода вертикального канала ИНС.

Учитывая это в структуру РИД КИМС включен блок предварительной обработки информации, решающий две главные задачи:

1) пересчет измерений ДИСС и РВ в инерциальную систему координат, используемую для навигации ЛА;

2) синхронизация по времени поступления сигналов комплексируемых устройств

В РИД КИМС для измерения вектора скорости осуществляется совместная обработка данных ИНС (W_ИН) и ДИСС (W_Д). Горизонтальные составляющие местоположения ЛА (координаты Х, Y) определяются по скорректированым измерениям горизонтальных каналов ИНС. Вертикальная составляющая местоположения ЛА определяется путем совместной обработки информации ИНС и РВ.

Для обеспечения оптимального комплексирования данных ИНС, ДИСС и РВ в структуру РИД КИМС включен фильтр Калмана. Рассмотрим структуру входного сигнала ФК исходя из следующего представления структуры выходных сигналов комплексируемых устройств.

W_ИН(t) = W(t)+ DWин(t),

где W_ИН = (W_XИН, W_YИН, W_ZИН)^T–вектор скорости ЛА, измеряемый с помощью ИНС, в инерциальной системе координат; W = (W_X, W_Y, W_Z)^T - вектор истинной путевой скорости ЛА; W_ИН = (DW_XИН, DW_YИН, DW_ZИН)^T - вектор ошибок измерения скорости с помощью ИНС

W_Д(t) = W(t)+ DWд(t),

W_Д = (W_XД, W_YД, W_ZД)^T–вектор скорости ЛА, измеряемый с помощью ДИСС, пересчитанный в инерциальную систему координат; W = (W_X, W_Y, W_Z)^T - вектор истинной путевой скорости ЛА; W_ИН = (DW_XД, DW_YД, DW_ZД)^T - вектор ошибок измерения скорости с помощью ИНС

Н_ИН(t) = Н(t)+ DНин(t),

Н_ИН(t)- высота поступающая с выхода вертикального канала ИНС; Н(t)- истинная высота над в инерциальной системе координат; DНин(t)- ошибка вертикального канала ИНС

Н_Р(t) = Н(t)+ DНр(t),

Н_Р(t)- высота поступающая с выхода РВ; Н(t)- истинная высота над в инерциальной системе координат; DНр(t)- ошибка измерения высоты с помощью РВ. Напомню, что такое представление выходного сигнала РВ справедливо лишь при полете ЛА на участком ровной поверхности, в противном случае в модель вектора состояния необходимо включать составляющую, характеризующую изменение рельефа поверхности.

С учетом приведенной модели выходных сигналов комплексируемых устройств, на вход ФК в соответствии с приведенной схемой комплексирования поступают:

1) разностный сигнал измерений ИНС и РВ:

r₁(t) = DHин(t) - DHр(t)

2) разностный сигнал ИНС и ДИСС:

r₂(t) = DWин(t) - DWд(t)

Учитывая, что ошибки ИНС изменяются существенно медленнее по сравнению с ошибками ДИСС и РВ, в качестве основной системы, ошибки которой будут компенсироваться используется ИНС.

Следовательно, на выходе ФК необходимо получить оптимальные оценки ошибок DX*ин(t), DY*ин(t), DH*ин(t), DW*_Xин(t), DW*_Yин(t), DW*_Zин(t),

Модель ошибок РИД КИМС: Для построения оптимального алгоритма ФК в РИД КИМС необходимо использовать модели ошибок ИНС, ДИСС и РВ.

Учитывая, что конкретный вид уравнений, описывающих ошибки ИНС зависит от того, какая система координат используется в качестве инерциальной системы координат ограничимся лишь анализом структуры модели ошибок ИНС.

Для моделирования случайных ошибок ИНС используется используется система дифференциальных уравнений, описывающая:

· ошибки Dx, Dy, DН_ин определения местоположения ЛА в инерциальной системе координат;

· ошибки DW_инx, DW_инy, DW_инz определения составляющих скорости ЛА;

· угловые ошибки Yx, Yy, Yz, ориентации осей гироплатформы ИНС относительно инерциальной системы координат;

· ошибки e_x, e_y, e_z – ошибки по скорости дрейфа гироскопов

· ошибки акселерометров DAx, DAz, DAy

В совокупности все перечисленные ошибки описываются системой из 15 линейных дифференциальных уравнений первого порядка относительно перечисленных компонент. Коэффициенты этих дифференциальных уравнений определяются в зависимости от конкретного вида системы координат, рассматриваемой в качестве инерциальной системы координат и характеристик формирующих фильтров, используемых для описания ошибок скорости дрейфа гироскопов (e_x, e_y, e_z) и ошибок акселерометров (DAx, DAz, DAy

Модель ошибок ДИСС включает в себя ошибки измерения составляющих путевой скорости ЛА: DW_дx, DW_дy, DW_{дz .} Для моделирования погрешностей ДИСС используется модель формирующего фильтра следующего вида:

DW_дx/dt= -a_x DW_дx +w_Wx

DW_дy/dt= -a_y DW_дy +w_Wy

DW_дz/dt= -a_z DW_дz +w_Wz

w_Wx, w_Wy, w_Wz - формирующие гауссовские белые шумы с нулевыми математическими ожиданиями и интенсивностями: N_Wx= 2a_xs_x; N_Wy= 2a_ys_y; N_Wy= 2a_ys_y;

Для моделирования погрешностей РВ используется модель формирующего фильтра следующего вида:

DН_р/dt= -b_р DН_р +w_р

w_р - формирующий гауссовский белый шум с нулевыми математическими ожиданиями и интенсивностью: N_р= 2b_рs_р

Таким образом в совокупности ошибки РИД КИМС в матричном виде могут быть описаны линейным дифференциальным уравнением следующего вида:

DX(t)/dt = FX(t) + Vw(t)

где X(t) - вектор состояния размерности (19 х 1) с компонентами:

X(t) = (Dx, Dy, DН_ин, DW_инx, DW_инy, DW_инz, Yx, Yy, Yz, e_x, e_y, e_z, DAx, DAz, DAy,

DW_дx, DW_дy, DW_дz, DHр)^Т

F- матрица размерности (19х19), определяющая динамику вектора состояния ФК;

w(t)- вектор формирующих белых шумов фильтра размером (10х1) с компонентами:

w(t)=(w_ex, w _{e, y} w_ez, w_Ax, w_{A, y} w_Az, w_Wx, w_Wy, w_Wz, w_р)

Компоненты вектора формирующих шумов имеют нулевые математические ожидания и задаются диагональной матрицей дисперсий Nw c элементами:

N_w(t)=diag(2a_exs_ex, 2a_eys_ey, 2a_ezs_ez, 2a_Axs_Ax, 2a_Ays_Ay, 2a_Azs_Az, 2a_xs_x, 2a_ys_y, 2a_zs_z, 2b_рs_р)

В соответствии со схемой комплексирования РИД КИМС на вход ФК поступает векторный сигнал r(t)=(r₁(t), r₂(t), r₃(t), r₄(t))^Т

r₁(t) = DH_ин(t) - DH_р(t)

r₂(t) = DW_инx(t) - DW_дx(t)

r₃(t) = DW_инy(t) - DW_дy(t)

r₄(t) = DW_инz(t) - DW_дz(t)

Тогда уравнение измерений ФК может быть представлено в виде:

r(t) = HX(t) +x(t)

где матрица H – матрица размером (4х19) с ненулевыми компонентами:

h₁₃=1; h₁₁₉=-1; h₂₄=1; h₂₁₆=-1; h₃₅=1; h₃₁₇=-1; h₄₆=1; h₄₁₈=-1;

x- вектор белых гауссовских шумов измерений РИД КИМС размером (4х1). В РИД КИМС в качестве шумов измерений выступают:

1) флуктационные ошибки РВ x₁=DH_рфл(t)

2) флуктационные ошибки ДИСС в каждом из каналов

x₂=DW_флx(t)

x₃=DW_флy(t)

x₄=DW_флz(t)

Такая структура вектора ошибок измерений обусловлена тем, что перечисленные ошибки имеют наиболее широкополосный спектр, а значит их аппроксимация гауссовским белым шумом вполне правомочна.

Предполагается, что шумы измерений имеют нулевые математические ожидания и характеризуются заданной диагональной матрицей интенсивности:

N_x(t)=diag(N_рфл, N_флx, N_флy, N_флz)

Сформированная математическая модель входного сигнала фильтра Калмана позволяет записать уравнения для оптимальных оценок вектора состояния X*(t) и апостериорной ковариационной матрицы ошибок К*_X(t), характеризующей ошибки оценивания.

С учетом вычисления оптимальных оценок вектора состояния на выходе РИД КИМС формируются оценки положения и составляющих вектора скорости ЛА:

X_РИД(t) = Х(t)+ DХ(t)- DХ*(t),

Y_РИД(t) = Y(t)+ DY(t)- DY*(t),

H_РИД(t) = H(t)+ DH_ин(t)- DH*ин(t),

W_РИДx(t) = W_x(t) - DW_инx(t) + DW*_инx(t)

W_РИДy(t) = W_y(t) - DW_инy(t) + DW*_инy(t)

W_РИДz(t) = W_z(t) - DW_инz(t) + DW*_инz(t)

Предполагая, что ошибки оценивания невелики, можно ожидать, что измеренные с помощью КИМС координаты местоположения ЛА и составляющие вектора скорости будут близки к истинным значениям.