Комплексная обработка навигационной информации в радиоинерциальном высотомере (РИВ).

Напомню, РВ измеряет истинную высоту относительно рельефа местности и имеет достаточно широкий спектр ошибок. ИИВ строится на основе вертикального канала ИНС, в котором измеряется вертикальное ускорение, а после двукратного интегрирования - высота ЛА. ИИВ имеет узкополосный характер спектральных погрешностей. Учитывая различие спектральных характеристик погрешностей ИИВ и РВ их комплексирование в структуре ИИВ может быть достигнуто на основе ранее рассмотренной схемы компенсации. При этом возможны два варианта реализации схемы компенсации:

разомкнутая схема;

замкнутая схема

Принцип построения радиоинерциального высотомера на основе разомкнутой схемы компенсации.

Структурная схема радиоинерциального измерителя высоты в этом случае имеет следующий вид;

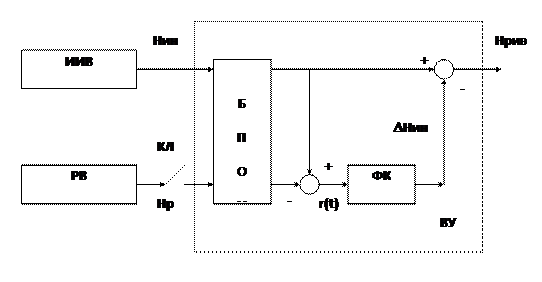
На схеме приведены:

Нин - значение высоты, поступающей с выхода инерциального измерителя высоты (ИИВ);

Нр - значение высоты, поступающей с выхода радиовысотомера (РВ). Наличие в схеме ключа КЛ условно показывает возможность дискретного поступления информации от РВ;

БПОИ - блок предварительной обработки информации. С помощью БПОИ показания РВ пересчитываются в единую систему координат, в которой осуществляется навигация ЛА.

ФК - фильтр Калмана. Заметим, что приведенная схема комплексирования эффективна при полете ЛА над поверхностью с практически неизменным средним уровнем (например, участки спокойной водной поверхности, равнинной местности). В этом случае сигналы с выхода ИИВ и РВ можно представить в следующем виде:

Hин(t) = H(t) + DHин(t)

Hр(t) = H(t) + DHр(t),

где H(t) - истинная высота ЛА в системе координат, используемой для навигации. В этом случае компенсация истинных высот H(t) в результате операции вычитания сигналов будет полной и сигнал, поступающий на вход ФК будет представлять собой разность ошибок измерителей высоты:

r(t) = DHин(t) - DHр(t)

ФК может быть реализован как в дискретном, так и в непрерывном времени. Если информация от измерителей поступает дискретно, то в БПОИ осуществляется синхронизация времени поступления сигналов на вход фильтра. Кроме того, для эффективной работы ФК в память вычислительного устройства ВУ закладывается информация о статистических характеристиках ошибок измерения комплексируемых навигационных устройств.

Так как, ошибки ИИВ существенно более медленноменяющиеся по сравнению с ошибками РВ, поэтому основным измерителем, погрешности которого, как наиболее медленно меняющиеся, компенсируются в радиоинерциальном высотомере рассматривается ИИВ. В этом случае в результате обработки поступающих данных ФК должен выдавать оптимальную (в смысле минимума среднеквадратической оценки) ошибку ИИВ DH*ин(t). Полученная в результате фильтрации оценка вычитается из выходного сигнала ИИВ. В результате осуществляется непрерывное отображение точной информации о высоте полета ЛА в блоке индикации и управления.

Учитывая, что ошибки ИИВ имеют тенденцию накапливаться в процессе движения ЛА, использование такой разомкнутой семы при построении комплексного измерителя высоты целесообразно для небольших интервалов времени.

Алгоритм оптимального ФК в радиоинерциальном высотомере. Основу рассмотренной нами структурной схемы РИВ составляет оптимальный фильтр Калмана. Рассмотрим его реализацию применительно к обработке сигналов РВ и ИИВ. Для этого запишем модель ошибок ИИВ и РВ. Упрощенная модель ошибок ИИВ в геоцентрической системе кординат описывается системой ДУ следующего вида

dDHин(t)/dt = DWz(t)

dDWz(t)/dt = (2g/R) DHин(t) + DAz + Dg

dDAz/dt = -aDAz +Na

dDg/dt = -b_gDg +Ng

Приведенная модель ошибок вертикального канала ИНС является упрощенной и записана при следующих предположениях:

не учитываются перекрестные связи между каналами ИНС. То есть предполагается, что ИИВ представляет собой вертикально установленный акселерометр, установленный на ГСП;

предполагается, что ошибки вносимые системой ориентации платформы в суммарную погрешность ИИВ существенно меньше других составляющих.

В приведенных уравнениях: DHин(t)- ошибка определения высоты с помощью ИИВ; DWz(t) - ошибка определения вертикальной скорости; слагаемое (2g/R)DHин(t) характеризует составляющую ошибки определения вертикальной скорости, вызванную неточностью определения ускорения силы тяжести из-за неопределенности местоположения ЛА; слагаемое DAz характеризует ошибки определения вертикальной скорости, обусловленные погрешностями акселерометра вертикального канала ИНС; слагаемое Dg характеризует ошибку определения вертикальной скорости, обусловленную неточностью определения ускорения силы тяжести из-за неточного знания гравитационного поля Земли. Показано, что ошибки DAz, Dg представляют собой гауссовские случайные процессы, который описывается стохастическими дифференциальными уравнениями. Na Ng- формирующие белые шумы.

Ошибки РВ описываются стохастическим дифференциальным уравнением следующего вида:

dHp(t)/dt = -bDHp +Np

Будем полагать, что высота Н < < R₀ полета значительно меньше радиуса Земли. То есть в приведенных уравнениях

R= R₀ + Н

является величиной постоянной.

Используя приведенные выражения запишем в векторной форме уравнения фильтра Калмана.

DX(t)/dt = F(t)X(t) + V(t)w(t)

где X(t) - вектор состояния размерности (5х1) с компонентами:

X(t) = (DHин, DWz, DAz, Dg, DHp)^Т

F(t) -матрица, описывающая динамику вектора состояния размерности (5х5) с элементами:

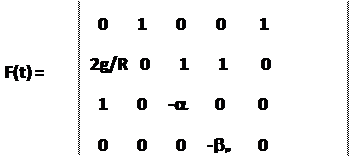
V(t) -матрица, коэффициентов шумов размерности (5х3) с элементами:

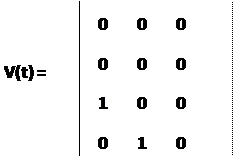
w(t) - вектор возмущений, представляющих собой центрированный белый шум размерности (3х1):

w(t) = (Na, Ng, Np)^Т]

c известной диагональной матрицей интенсивностей:

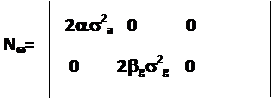
Для серийных измерителей элементы матрицы интенсивностей имеют следующие значения:

a=10^-3[1/c]

s²_a=10^-6[м²/с⁴]

b_g =0.5х10^-2[1/c]

s² _g =10^-8[м²/с⁴]

b=10^-1[1/c]

s²_р=10³[м²]

Согласно приведенной схеме радиоинерциального высотомера уравнение измерений ФК, описывающее наблюдаемый на входе фильтра сигнал записывается в виде:

r(t) = H(t)X(t) + x(t)

где - матрица измерений размерности (1х5) с элементами H(t) = (1 0 0 0 -1); - центрированный белый шум с известной интенсивностью N_x.

В предыдущей части нашего курса мы рассмотрели структуру оптимального ФК, которая для рассматриваемого радиоинерциального высотомера имеет вид:

DX*(t)/dt = F(t)X*(t) + Кф(t)[r(t)-H(t)X*(t)]

Кф(t)- коэффициент усиления фильтра:

К_ф(t) =K*(t)H(t)/N_x.

K*(t) - ковариационная матрица ошибок оценивания, описываемая уравнением Риккати:

dK*(t)/dt = F(t)K*(t)+ K*(t)F^Т(t)- K*(t)H^Т(t) H(T)K*(t)/ N_x +V(t)N_wV^Т(t)

Начальные условия для приведенного ФК:

X*(0) = (0, 0, 0, 0, 0)^Т

K*(0) =М[X(0) X ^Т(0)]

Ковариационная матрица характеризует неопределенность знания начального состояния или степень точности задания начальной оценки X*(0). Если предположить, что начальная выставка ИИВ осуществляется по данным РВ, то неточность этой выставки можно охарактеризовать погрешностью измерения высоты в РВ, которая характеризуется дисперсией s²_p. Тогда учитывая, что составляющие ошибок измерителей статистически независимы, начальная ковариационная матрица может быть представлена в следующем виде:

Замечание. Мы рассмотрели реализацию ФК, основанную на предположении, что полет ЛА происходит над ровной поверхностью. В общем случае полета ЛА средний уровень поверхности может изменяться и показания РВ будут отличаться от показаний ИИВ. В этом случае в уравнении описывающем переменные состояния фильтра должна появиться дополнительная случайная составляющая Нотн(t) = Нотн(t)-Н(t), которая характеризует изменение рельефа местности относительно поверхности земного эллипсоида. Ранее мы рассматривали различные модели позволяющие описать этот случайный показатель для различных типовых рельефов местности. В первом приближении изменение рельефа местности можно описать стационарным случайным процессом, задаваемым уравнением:

DHотн/dt = -t_HHотн(t) +N_H(t)

где – центрированный гауссовский белый шум, корреляционная функция которого предполагается известной.

Для реализации алгоритма ФК в данном случае система уравнений, описывающих ошибки ИИВ и РВ должна дополниться уравнением для Hотн и вектор состояния фильтра в этом случае буде включать шесть элементов:

X(t) = (DHин, DWz, DAz, Dg, DHp, Hотн)^Т

Дальнейшая формализация уравнений ФК полностью соответствует рассмотренной ранее.

Принцип построения радиоинерциального высотомера на основе замкнутой схемы компенсации.

Рассматривая схему радиоинерциального высотомера, построенного на основе разомкнутой схемы компенсации мы отметили, что его использование для решения навигационной задачи целесообразно для небольших отрезков времени. Для обеспечения качественной работы радиоинерциального высотомера в течение длительного времени необходимо использовать замкнутую схему построения комплексного радиоинерциального высотомера Структурная схема радиоинерциального измерителя высоты в этом случае имеет следующий вид;

Отличие данной схемы от разомкнутой схемы компенсации заключается в том, что в данном случае ФК включается в цепь обратной связи. Сигналы обратной связи фильтра, обозначенные на схеме используются как для коррекции ошибок ИИВ так и РВ. Если сигнал обратной связи используется только для коррекции накапливающихся ошибок ИИВ, то такой вариант комплексирования будет смешанным: по отношению к ИИВ схема будет замкнутой, а по отношению к РВ - разомкнутой. Наличие сигналов обратной связи по отношению к ИИВ позволяет осуществлять коррекцию накапливающихся ошибок измерителя и тем самым автоматически поддерживать их малыми на всем интервале функционирования РИВ.

Будем по-прежнему предполагать, что инерциальный измеритель работает непрерывно и определяет навигационную высоту с ошибкой DHин(t):

Hин(t)= H(t)+ DHин(t).

Радиовысотомер также работает непрерывно и измеряет истинную высоту относительно рельефа:

Hр(t)= H(t)+ DHр(t).

Входным сигналом фильтра, как и для разомкнутой схемы компенсации служит разностный сигнал:

r₀(t)= Hин(t) - Hp(t).

Коррекция накапливающихся ошибок ИИВ в данном случае достигается за счет того, что выходной сигнал фильтра Калмана представляет собой разность DHин(t)- DH*ин(t), где DH*ин(t) – оптимальная оценка ошибки измерения высоты с помощью ИИВ. То есть в качестве выходного сигнала фильтра используется не оценка ошибки измерения высоты, а ошибка оценки фильтра. Такая структура корректирующего сигнала позволяет компенсировать накапливающуюся ошибку ИИВ. Действительно, ошибка измерения высоты с учетом коррекции:

Hин(t)= H(t)+ DHин(t)- DHин(t)+ DH*ин(t)= H(t)+ DH*ин(t)

в этом случае не превышает ошибку оптимальной оценки фильтра Калмана.

Алгоритм оптимального ФК в радиоинерциальном высотомере, реализованном на основе закнутой схемы компенсации.

Рассмотрим особенности реализации ФК применительно к обработке сигналов РВ и ИИВ в рамках замкнутой схемы. Для этого вернемся к уравнениям, описывающие динамику вектора состояния:

dX(t)/dt = F(t)X(t) +V(t)w(t)

X(t) -вектор состояния с компонентами X(t) = (DHин, DWz, DAz, Dg, DHp)^Т

Предполагается, что ошибки измерений ИИВ и РВ описываются такжке, как в случае разомкнутой системы

dDHин(t)/dt = DWz(t)

dDWz(t)/dt = (2g/R) DHин(t) + DAz + Dg

dDAz/dt = -aDAz +Na

dDg/dt = -b_gDg +Ng

dHp(t)/dt = -bDHp +Np

Введем вектор X*(t), представляющий экстраполированную оптимальную оценку вектора состояния. Эта экстраполированная оценка может быть получена как результат решения следующего уравнения:

DX*(t)/dt = F(t)X*(t)

Введем новый вектор состояния X0(t)= X(t)- X*(t)

Уравнение описывающее новый вектор состояния имеет вид:

dX₀(t)/dt = F(t)X₀(t) + V(t)w(t)

где X₀(t) - вектор состояния фильтра в замкнутой системе X₀(t) = X(t) - X*(t) с компонентами:

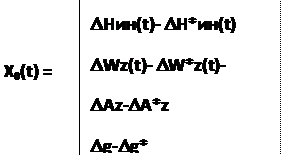
Входной сигнал r₀(t), поступающий на вход фильтра, в этом случае равен:

r₀(t) =(DHин(t)- DH*ин(t))- (DHр(t)- DH*р(t))

Тогда уравнение измерений ФК, описывающее наблюдаемый на входе фильтра сигнал в векторном виде можно представить следующим образом:

r₀(t) = H(t)X₀(t) + x(t)

H(t)=(1 0 0 0 –1)

Дальнейшая реализация алгоритма фильтра Калмана с учетом перехода к вектору состояния X₀(t) полностью аналогична структуре оптимального алгоритма, рассмотренного для случая разомкнутой схемы компенсации. Отличие состоит в том, что вектор состояния ФК в случае замкнутой схемы представляет собой вектор ошибок оптимальных оценок фильтра (а не оценок ошибок измерителей!!!!!), то есть введение корректирующих воздействий обеспечивает выработку значений высоты в комплексном радиоинерциальном высотомере с погрешностями равными, ошибкам оптимальных оценок фильтра Калмана.

С учетом структуры вертикального канала ИНС оптимальные оценки корректирующего сигнала, поступающего с выхода ФК в дальнейшем используются для коррекции накапливающихся ошибок ИНС. Эта коррекция производится в соответствии со следующей схемой:

6.3 Комплексный радиобаровысотомер (РБВ).

Одним из эффективных путей построения КСИВ является использование в их составе РВ и БВ. Это обусловлено тем, что ошибки БВ в силу физических принципов работы сосредоточены в основном в низкочастотной области спектра, а РВ, как мы уже отмечали, имеет широкополосный спектр ошибок. То есть в данном случае так же, как и для РИВ, выполняется обязательное условие получения выигрыша при комплексировании, а именно, различие спектральных характеристик ошибок измерителей, входящих в состав комплексной системы.

Комплексная обработка навигационной информации в радиобаровысотомере (РБВ).

Учитывая различие спектральных характеристик ошибок БВ и РВ их комплексирование в структуре РБВ может быть достигнуто на основе ранее рассмотренной схемы компенсации.

Структурная схема радиобаровысотомера в этом случае имеет следующий вид;

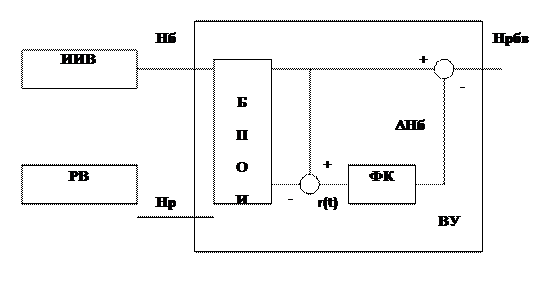
На схеме приведены:

Нб - значение высоты, поступающей с выхода баровысотомера (БВ);

Нр - значение высоты, поступающей с выхода радиовысотомера (РВ). С помощью БПОИ показания РВ пересчитываются в единую систему координат, в которой осуществляется навигация ЛА.

ФК - фильтр Калмана.

Предполагается, что выходные сигналы РВ и БВ могут быть представлены в следующем виде:

Hб(t) = H(t) + DHб(t)

Hр(t) = H(t) + DHр(t),

где H(t) - истинная высота ЛА в системе координат, используемой для навигации.

Сигнал, поступающий на вход ФК в соответствие с приведенной структурной схемой будет представлять собой разность ошибок измерителей высоты:

r(t) = DHб(t) - DHр(t)

Выходом ФК в этом случае является оптимальная (в смысле минимума среднеквадратической оценки) ошибка DH*б(t). Полученная в результате фильтрации оценка вычитается из выходного сигнала баровысотомера. В результате осуществляется непрерывное отображение точной информации о высоте полета ЛА в блоке индикации и управления.

Рассмотрим структуру алгоритма комплексной обработки навигационной информации применительно к радиобаровысотомеру. Основу алгоритма составляет модель ошибок измерений комплексируемых измерителей. Рассмотрим ее более подробно.

Модель ошибок БВ: Как известно принцип работы БВ основан на измерении на борту ЛА давления атмосферы, а на его основе высоты полета с использованием известных зависимостей зависимостей, связывающих давление и высоту над поверхностью земли.

Погрешность измерений БВ DHб(t) в линейном приближении может быть представлена в следующем виде:

DHб(t)= DHм(t)+ DHд(t) +DHап(t),

где DHм(t) - методическая составляющая погрешности измерений; DHд(t) - динамическая составляющая погрешности измерений; DHап(t) - аппаратурная составляющая погрешности измерений БВ

Методическая погрешность БВ DHм(t)= DHст(t)+DHсин(t) включает следующие составляющие:

составляющую DHст(t), обусловленную случайными колебаниями давления в вертикальном направлении, вызванными отличием параметров атмосферы от стандартных значений;

составляющую DHсин(t), обусловленную колебаниями давления в горизонтальном направлении из-за синоптических явлений.

Показано, что составляющая DHст(t) может быть представлена в виде стационарного случайного процесса, описываемого системой стохастических дифференциальных уравнений следующего вида:

dDHст(t)/dt = Fст(t),

dFст(t)/dt= - (0.67Wв +a_ст) Fст(t) - (0.67Wвa_ст) DHст(t)+3.2 10⁴a_стw_ст(t),

где 1/a_ст - интервал корреляции случайного процесса DHст(t), который для серийных БВ лежит в диапазоне 45-150 с. С.к.о. случайного процесса DHст(t) оценивается величиной sст=400-600м. Wв - вертикальная скорость ЛА; w_ст(t)- формирующийбелый шум с нулевым математическим ожиданием и единичной интенсивностью

Составляющая DHсин(t) может быть представлена в виде стационарного случайного процесса, описываемого системой стохастических дифференциальных уравнений следующего вида:

dDHсин(t)/dt = Fсин(t) + w_син(t),

dFсин(t)/dt=- (a_син+w₀) DHсин(t) - 2a_син Fсин(t) + {(a²_син+w²₀)^1/2- 2a_син}w_син(t),

где 1/a_син - интервал корреляции случайного процесса DHсин(t), который для серийных БВ лежит в диапазоне (10-15)10³ с; w₀=2х10⁴ рад/с. С.к.о. случайного процесса DHсин(t) оценивается величиной sсин=100-200м. - вертикальная скорость ЛА; w_син(t)- - формирующийбелый шум с нулевым математическим ожиданием и единичной интенсивностью

Аппаратурная погрешность БВ DHап(t) обусловлена наличием вязкого трения в воздуховоде БВ DHтр(t) и случайными колебаниями температуры атмосферы DHт(t) относительно стандартных значений.

Погрешность DHтр(t) может быть аппроксимирована стационарным случайным процессом, описываемым системой дифференциальных уравнений следующего вида:

dDHтр(t)/dt = Fтр(t),

dFтр(t)/dt= - a_тр Fтр(t) + Ктрa_трw_тр(t),

где 1/a_тр - постоянная времени запаздывания в воздуховоде БВ, который для серийных БВ достигает 1 с. Ктр - постоянный коэффициент, зависящий от высоты полета и горизонтальной скорости. Дисперсия случайного процесса DHтр(t) оценивается величиной s²_тр=1200 м². w_тр(t)- - формирующийбелый шум с нулевым математическим ожиданием и единичной интенсивностью.

Вторая составляющая аппаратурной погрешности БВ это температурная погрешность DHт(t), обусловленная случайными колебаниями температуры воздуха относительно стандартных значений. Эта составляющая представляет собой медленноменяющуюся случайную функцию, которая описывается дифференциальным уравнением вида:

dDHт(t)/dt = 0.

Динамическая погрешность БВ DHдин(t) обусловлена инерционностью измерителя по отношению к изменениям измеряемого параметра. Эта погрешность описывается стохастическим дифференциальным уравнением:

dDHдин(t)/dt = - a_динw_дин(t),

где 1/a_дин - интервал корреляции случайного процесса DHдин(t), w_дин(t)- - формирующийбелый шум с нулевым математическим ожиданием и единичной интенсивностью

Модель ошибок РВ. Среди погрешностей РВ наибольшее значение имеет смещение оценки высоты полета DHр(t),, вызванное сменой рельефа местности по трассе полета ЛА и случайными эволюциями по крену и тангажу. Погрешность РВ описывается ДУ вида:

dDHр(t)/dt = - bDHр + w_р(t),

где 1/b - интервал корреляции случайного процесса DHр(t),, который для серийных РВ достигает 10 с. Дисперсия случайного процесса DHр(t) оценивается величиной s²_р=1000 м². w_р(t)- - формирующийбелый шум с нулевым математическим ожиданием и интенсивностью 2bs²_p.

Алгоритм оптимального ФК в радиобаровысотомере..

Используя рассмотренную модель ошибок БВ и РВ

dDHст(t)/dt = Fст(t)

dFст(t)/dt= - (0.67Wв +a_ст) Fст(t) - (0.67Wвa_ст) DHст(t)+3.2 10⁴a_стw_ст(t)

dDHсин(t)/dt = Fсин(t) + w_син(t)

dFсин(t)/dt=- (a_син+w₀) DHсин(t) - 2a_син Fсин(t) + {(a²_син+w²₀)^1/2- 2a_син}w_син(t)

dDHтр(t)/dt = Fтр(t)

dFтр(t)/dt= - a_тр Fтр(t) + Ктрa_трw_тр(t)

dDHт(t)/dt = 0

dDHдин(t)/dt = - a_динw_дин(t)

dDHр(t)/dt = - bDHр + w_р(t),

Запишем в векторной форме уравнения фильтра Калмана.

DX(t)/dt = F(t)X(t) + V(t)w(t)

где X(t) - вектор состояния размерности (9 х 1) с компонентами:

X(t) = (DHст, Fст, DHсин, Fсин, DHтр, Fтр, DHт, DHдин, DHр)^Т

F(t) -динамическая матрица фильтра, ненулевые элементы которой равны:

f₁₂ =1; f₂₁ = - 0.67Wвa_ст; f₂₂ = - 0.67Wв+a_ст; f₃₄ =1; f₄₃ =- (a_син+w₀); f₄₄ =-2a_син;

f₅₆ =1; f₆₆ =-a_тр; f₉₉ =-b

w(t)=(w_ст, w_син , w_тр, w_дин, w_р)^Т - вектор формирующих белых шумов размерности (5х1)с нулевым математическим ожиданием и матрицей интенсивности:

V(t) -матрица, коэффициентов шумов размерности (9х5) с элементами:

Согласно приведенной схеме радиобаровысотомера уравнение измерений ФК, описывающее наблюдаемый на входе фильтра сигнал записывается в виде:

r(t) =DHм(t)+ DHд(t) +DHап(t)- DHр(t) = DHст+DHсин+DHтр+DHт + DHдин - DHр,

или в векторном виде:

r(t) = H(t)X(t) + x(t)

где H(t) - матрица измерений размерности (1х9) с элементами:

H(t) = (1 0 1 0 1 0 1 1 -1); x(t) - центрированный белый шум с известной интенсивностью N_x.

С учетом проведенной формализации модели структура оптимального ФК для рассматриваемого радиобаровысотомера имеет вид:

DX*(t)/dt = F(t)X*(t) + Кф(t)[r(t)-H(t)X*(t)]

Кф(t)- коэффициент усиления фильтра:

К_ф(t) =K*(t)H(t)/N_x.

K*(t) - ковариационная матрица ошибок оценивания, описываемая уравнением Риккати:

dK*(t)/dt = F(t)K*(t)+ K*(t)F^Т(t)- K*(t)H^Т(t) H(T)K*(t)/ N_x +V(t)N_wV^Т(t)

Начальные условия для приведенного ФК:

X*(0) = (0, 0, 0, 0, 0, 0, 0, 0, 0)^Т

K*(0) =М[X(0) X ^Т(0)]

Начальная ковариационная матрица K*(0) имеетвид:

Таким образом, на выходе фильтра Калмана формируются оптимальные оценки ошибок баровысотомера DH*ст+DH*син+DH*тр+DH*т + DH*дин, которые в последующем вычитаются из измерения высоты Hб(t) = H(t) + DHб(t).

Тем самым обеспечивается получение оценки высоты, близкой к истинному значению:

H_рбв(t)=H(t)+DHст+DHсин+DHтр+DHт + DHдин -(DH*ст+DH*син+DH*тр+DH*т + DH*дин)

H_рбв(t)» H(t)