
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Величина як властивість предметів або явищ реального світу. Вимірювання величин. Властивості скалярних величин.
|
|
У до числовий період діти ознайомлюються з деякими властивостями предметів (колір, розмір, форма і т.д.). У ході дослідження вони приходять до висновку, що деякі предмети, які мають однакову форму, однакового кольору, виготовлені з однакового матеріалу, мають ще деяку властивість, якою відрізняються один від одного. Наприклад, смужки однакового кольору, однакової ширини відрізняються довжиною (довша, коротша). Або два кубики (мають однакову форму) однакового кольору і однакових розмірів відрізняються за масою.
Отже, величина – це особлива властивість реальних об’єктів або явищ.
Величини бувають одного роду (виражають однакові властивості наприклад, довжини конкретних об’єктів) і різного роду (виражають різні властивості, наприклад, масу і об’єм предмета).
Порівнюючи предмети безпосередньо, ми можемо зробити висновок про рівність чи нерівність (більше або менше) цих величин. Уточнити ж відповідь можна шляхом вимірювання. Виміряти величину – означає порівняти її з деякою іншою величиною цього ж роду, яку прийнято за одиницю.
Якщо дано деяку величину а і вибрана одиниця цієї величини е, то в результаті вимірювання а знаходиться таке дійсне число х, що а = х · е. Число х називається числовим значенням величини а при одиниці вимірювання е. Коротко це записується так: х = те (а).
Справді, 5кг = 5 · 1кг, 12см = 12 · 1см, 3год = 3 · 1год.
Величини, які повністю визначаються їх числовими значеннями, називаються скалярними величинами (маса, площа, довжина, об’єм). Існують ще й векторні величини (мають напрямок).
Скалярні величини мають такі властивості:
1. Будь-які дві величини одного роду можна порівнювати (наприклад, довжина гіпотенузи більша за довжину будь-якого катета, маса яблука менша від маси кавуна, довжини протилежних сторін прямокутника однакові).
2. Величини одного роду можна додавати. В результаті одержуємо величину цього самого роду, яку називають сумою величин і позначають як a + b.
3. Величину можна помножити на дійсне число. Одержимо величину цього ж роду: b = x · a, яка називається добутком величини а і числа х.
4. Величини одного роду можна віднімати: a – b = c, де a = c + b.
5. Величини одного роду можна ділити. При цьому одержується невід’ємне дійсне число х, яке називається часткою величин a, b:
a: b = x, де a = b ·x.
Число х ще називають часткою величин a, b.
Вимірювання величин дає змогу виконувати операції над їх числовими значеннями:
- Якщо величини a, b виміряні за допомогою тієї самої одиниці величини е, то відношення між ними будуть такі ж, як і між їхніми числовими значеннями:
 ;
; 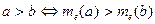 ;
; 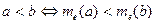 .
.
- Якщо величини a, b виміряні за допомогою тієї самої одиниці величини е, то, щоб знайти числове значення величини a + b, достатньо додати їх числові значення:
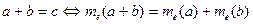 .
.
- Якщо величини a, b такі, що b = х · а, де х – додатне дійсне число і величина а виміряна за допомогою одиниці вимірювання е, то
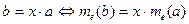 .
.