Многокутник, його елементи. Формули для обчислення площ фігур.

Об’єднання простої замкненої лінії та її внутрішньої області називається многокутником. Ланки ламаної називаються сторонами многокутника. Точки, в яких збігаються дві суміжні ланки, називаються вершинами многокутника. Відрізок, що з’єднує дві вершини многокутника, які не належать одній з його сторін, називається діагоналлю.

Залежно від кількості сторін многокутник називається трикутником, чотирикутником, п’ятикутником тощо.

Для обчислення площ многокутників використовуються такі формули:

прямокутник: 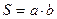, де a, b – сторони прямокутника;

, де d – діагональ прямокутника, φ – кут між діагоналями;

квадрат: , де а – сторона квадрата;

, де d – діагональ квадрата;

паралелограм: 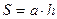, де а – сторона паралелограма, h – висота, проведена до цієї сторони;

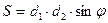, де d₁, d₂ – діагоналі паралелограма, φ – кут між діагоналями;

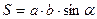, де a, b – сторони паралелограма, α – кут паралелограма;

ромб: 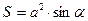, де a – сторона ромба, α – кут ромба;

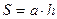, де а – сторона ромба, h – висота, проведена до цієї сторони;

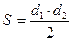, де d₁, d₂ – діагоналі ромба;

трапеція: , де a, b – основи трапеції, h – її висота;

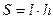, де l – середня лінія трапеції, h – її висота;

трикутник: 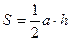, де а – сторона трикутника, h – висота, проведена до цієї сторони;

, де a, b – сторони трикутника, α – кут між ними;

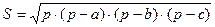, де р – півпериметр трикутника (формула Герона);

правильний (рівносторонній) трикутник: ;

прямокутний трикутник: , де a, b – катети цього трикутника.

Площу круга обчислюють за формулами: , де R - його радіус;

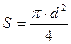, де d – діаметр круга.

Площі поверхонь геометричних тіл знаходять за такими формулами:

пряма призма:

бічна поверхня 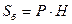, де Р – периметр основи призми, Н – її висота (бічне ребро);

повна поверхня , де 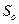– площа основи призми;

правильна піраміда:

бічна поверхня 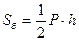, де Р – периметр основи піраміди, h – апофема (висота бічної грані);

повна поверхня , де 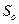– площа основи піраміди;

циліндр:

бічна поверхня 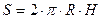, де R - радіус основи циліндра, Н – висота (твірна); повна поверхня ;

конус: бічна поверхня , де R - радіус основи конуса, l – його твірна;

повна поверхня ;

сфера: 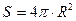, де R - радіус сфери (кулі).