
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Разложение силы
|
|
Задача о разложении данной силы на две или несколько составляющих может оказаться неопределенной, так как разложить данную силу на две и более составляющих, лежащих с ней в одной плоскости, можно бесчисленным множеством способов, путем построения сколько угодно параллелограммов для которых данная сила будет служит диагональю. Для того чтобы задача стала определенной необходимы некоторые дополнительные условия. Всего на плосоксти может быть два случая:
1. Разложить данную силу F на две силы по двум заданным направлениям, лежащим с ней в одной плоскости.
Для этого достаточно из конца вектора F провести прямые, параллельные данным прямым I и II (рис.2.5), до их пересечения с этими прямыми в точках В и С. Векторы  и
и 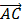 определяют искомые составляющие силы.
определяют искомые составляющие силы.
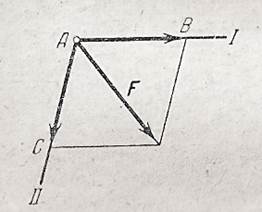
Рис.2.5.
2. Разложить данную силу F на две силы, лежащие с ней в одной плоскости и имеющие заданные численные значения.
Из начала А и конца В вектора F (рис.2.6) проводим две дуги радиусами, равными в выбранном масштабе заданными значениями F1 и F2. Эти дуги пересекутся в точках С и D. Дополним треугольники АСВ и АDВ до соответствующих параллелограммов, в которых АВ является диагональю. Тогда векторы 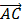 и
и  или
или 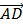 и
и  определят искомые составляющие силы. Очевидно, что эта задача имеет два возможных решения.
определят искомые составляющие силы. Очевидно, что эта задача имеет два возможных решения.
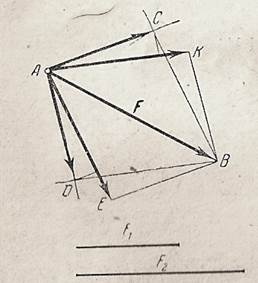
Рис.2.6.
Разложение силы на три составляющих силы по трем заданным направлениям, не параллельным одной плоскости (например, по трем взаимно перпендикулярным координатным осям). Для этого на основании правила параллелепипеда, достаточно построить такой параллелепипед, ребра которого имели бы заданные направления и, диагональю которого являлась бы данная сила (рис.2.3)