Аналитический способ сложения сил

Правило силового многоугольника позволяет геометрическим построением определить модуль и направление равнодействующей данной системы сходящихся сил. Аналитическое решение этой задачи основано на применении метода проекций и базируется на теореме о проекции равнодействующей силы на ось:

Проекция равнодействующей на какую либо ось равна алгебраической сумме проекций составляющих сил на ту же ось.

Пусть для данных сил 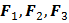построен силовой многоугольник и пусть 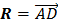(рис.2.11). Спроектируем все силы на данную ось х. Для чего проведем через начало и конец каждой силы плоскости, перпендикулярные к оси х. Пусть эти плоскости пересекают ось х в точках а, b, с и d.

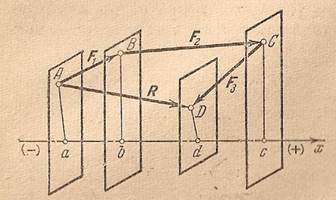
Рис.2.11

Тогда получим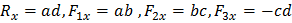

Сложив эти равенства, получим: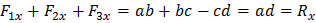

Возьмем систему сходящихся сил, заданных своими проекциями на координатные оси. Обозначим эти проекции соответствующими заглавными буквами:

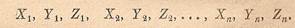Требуется определить модуль и направление равнодействующей. Обозначив искомую равнодействующую через R и ее проекции через 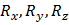, согласно теореме о проекции равнодействующей получим:

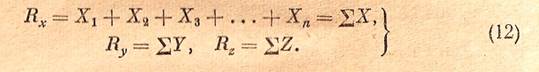
Величина R определяется по формуле (2.3):

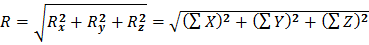(2.13)

Чтобы определить направление равнодействующей, нужно найти ее углы с координатными осями. Обозначив эти углы через α, β, γ на основании формулы (2.5) получим:

Равенства (2.13) и (2.14) представляют собой формулы для определения модуля и направления равнодействующей по заданным проекциям составляющих сил.

Из равенства (2.11) и (2.12) следует, что формула разложения равнодействующей по координатным осям имеет следующий вид:

После того как найдены модуль и направление равнодействующей сходящихся сил, можно найти и линию действия равнодействующей. Для этого надо составить уравнение прямой, проходящей через точку пересечения линий действия данных сил и имеющей направление их равнодействующей. По правилам аналитической геометрии получаем это уравнение в виде:

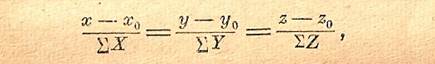
В формуле разложения вектора по координатным осям (2.15) коэффициенты при i, j, k представляют собой проекции этого вектора на соответствующие оси, следовательно, из равенства (2.15) находим, что

Проекция суммы данных векторов на какую-нибудь ось равна алгебраической сумме проекций слагаемых векторов на ту же ось.