
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Проекция вектора на ось
|
|
Пусть имеем вектор 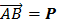 и некоторую ось х. Проведем через начало и конец вектора плоскости, перпендикулярные к оси х и пересекающие эту ось в точках а и b (рис.2.7). Эти точки называются проекциями точек А и В на ось х, а длина отрезка аb, взятая с соответствующим знаком, называется проекцией вектора
и некоторую ось х. Проведем через начало и конец вектора плоскости, перпендикулярные к оси х и пересекающие эту ось в точках а и b (рис.2.7). Эти точки называются проекциями точек А и В на ось х, а длина отрезка аb, взятая с соответствующим знаком, называется проекцией вектора  на ту же ось. Проекция вектора на ось представляет собой алгебраическую скалярную величину; ей приписывается знак +если направление вектора совпадает с направлением данной оси, в противном случае проекция отрицательна:
на ту же ось. Проекция вектора на ось представляет собой алгебраическую скалярную величину; ей приписывается знак +если направление вектора совпадает с направлением данной оси, в противном случае проекция отрицательна:
прхР=Рх=аb

Рис.2.7.
Проведем через точку А начала вектора Р прямую, параллельную оси проекций; эта прямая пересечет плоскость Вb в точке С. Так как прямая АС перпендикулярна плоскости Вb, то в треугольнике АВС угол С прямой; угол ВАС=α – угол между вектором Р и положительным направлением оси проекций. Из треугольника АВС получаем:
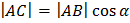 , т.к.
, т.к. 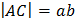 , то
, то 
Полученное выражение для проекции вектора на ось определяет не только абсолютную величину, но и знак проекции. В рассматриваемом случае проекция Рх положительна, а угол α – острый; следовательно, его косинус также положительный. В случае отрицательной проекции (рис.2.8) из треугольника А1В1С1 имеем:

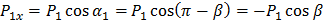
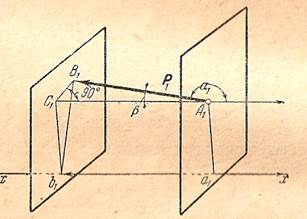
Рис.2.8.
Проекция вектора на ось равна (по абсолютной величине и по знаку) произведению модуля вектора на косинус угла между этим вектором и положительным направлением оси проекций.
Из определения проекции вектора на ось следует, что проекция не изменится, если мы будем переносить вектор параллельно самому себе или если будем проектировать его на различные, но параллельные и одинаково направленные оси.
Возьмем прямоугольную систему координат О хуz и некоторый вектор 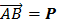 рис.2.9.
рис.2.9.

Рис.2.9.
Проведем через точку А оси Ах', Ау' и Аz', параллельные данным координатным осям, и построим на новых осях прямоугольный параллелепипед, для которого вектор  является диагональю. Длины выходящих из вершины А ребер этого параллелепипеда, взятые с соответствующими знаками, представляют собой проекции вектора
является диагональю. Длины выходящих из вершины А ребер этого параллелепипеда, взятые с соответствующими знаками, представляют собой проекции вектора  на оси Ах', Ау' и Аz', или, что одно и то же, на оси Ох, Оу и Оz. Обозначая эти проекции через Рх, Ру и Рz получим
на оси Ах', Ау' и Аz', или, что одно и то же, на оси Ох, Оу и Оz. Обозначая эти проекции через Рх, Ру и Рz получим 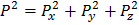 , откуда
, откуда
 (2.3)
(2.3)
Обозначим углы вектора Р с координатными осями х, у, z соответственно через α, β и γ, будем иметь:
 ,
,  ,
,  (2.4)
(2.4)
Откуда
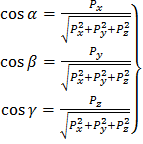 (2.5)
(2.5)
Формулы (2.3) и (2.5) позволяют аналитически определить величину и направление вектора по трем заданным его проекциям на координатные оси. В этих формулах перед радикалами необходимо брать знак +, так как модуль вектора – величина положительная.