Умножение вектора на скаляр. Единичный вектор

Умножить вектор Р на положительный скалярный множитель λ – это значит построить новый вектор Р ₁, модуль которого равен λ Р и который имеет тоже направление, что и вектор Р: 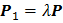(2.6)

Если множитель λ отрицателен, то направление вектора Р ₁ будет противоположно направлению вектора Р, а модуль вектора Р ₁ в этом случае будет равен 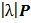, где 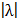обозначает абсолютную величину множителя λ. Таким образом, два вектора Р и 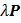всегда параллельны или расположены на одной прямой. Такие векторы называются коллинеарными.

Если λ > 0, то параллельные векторы Р ₁ и Р направлены в одну сторону и образуют с положительным направлением оси х один и тот же угол α. Откуда:

Аналогично получим: 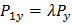и 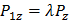. Из полученных равенств следует:

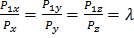(2.7)

Т.е. проекции параллельных векторов на координатные оси пропорциональны. Соотношение (2.6) равносильно трем скалярным соотношениям (2.7)

Вектор, направление которого совпадает с направлением данного вектора Р и модуль которого равен единице, называется единичным вектором Р⁰ =1 данного вектора Р. Между этими векторами существует зависимость 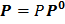(2.8)

Вектор можно представить в виде произведения его модуля на его единичный вектор.