Основных интегралов

Функция F (x) называется первообразной функции f (x) на некотором промежутке 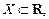если F (x) дифференцируема на промежутке X и для всех 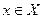выполняется

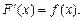(19.1)

Если F (x) – одна из первообразных функции f (x) на промежутке X, то любая другая ее первообразная имеет вид где C – произвольная постоянная.

Совокупность всех первообразных функции f (x) называется неопределенным интегралом от функции f (x):

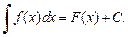(19.2)

В равенстве (19.2) использован знак интеграла 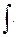Функция f (x) называется подынтегральной функцией, f (x) dx – подынтегральное выражение, x – переменная интегрирования.

Операция нахождения всех первообразных функции f (x) называется интегрированием этой функции.

Всякая непрерывная на множестве X функция имеет на этом множестве первообразную, а значит, неопределенный интеграл.

Геометрически неопределенный интеграл представляет собой семейство кривых 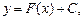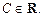График каждой первообразной называется интегральной кривой.

Таблица основных интегралов:

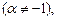(19.3)

в частности,

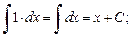(19.4)

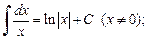(19.5)

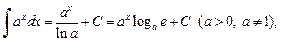(19.6)

в частности,

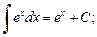(19.7)

(19.8)

(19.9)

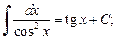(19.10)

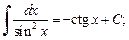(19.11)

(19.12)

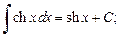
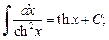
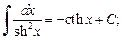
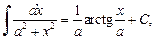(19.13)

в частности,

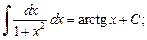
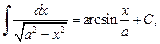(19.14)

в частности,

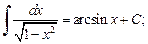
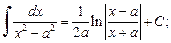(19.15)

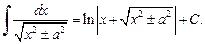(19.16)