Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод поднесения под знак дифференциала
|
|
Для вычисления интеграла используют определение дифференциала:
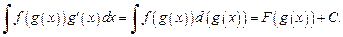
Согласно этому методу не делают явно замену переменной, подразумевая, что g (x) играет роль новой независимой переменной.
При использовании метода поднесения под знак дифференциала, метода замены переменной, метода подстановки удобно использовать простейшие преобразования дифференциала:
1) 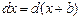 (b – произвольная постоянная величина);
(b – произвольная постоянная величина);
2) 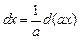 (постоянная
(постоянная  );
);
3) 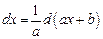 (постоянная
(постоянная 
Пример 1. Найти неопределенный интеграл:
1) 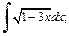 2)
2) 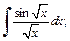 3)
3) 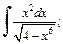 4)
4) 
Решение. 1) 1-й способ. Используем метод замены переменной. Положим  Тогда
Тогда 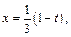
 Имеем:
Имеем:
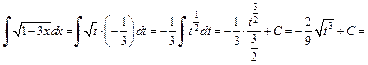
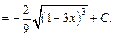
Для вычисления интеграла использовали формулу (19.3) таблицы неопределенных интегралов.
2-й способ. Используем метод поднесения под знак дифференциала. Представим данный интеграл в следующем виде:
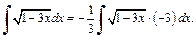
Учитывая, что  по формуле (19.3) таблицы неопределенных интегралов получаем:
по формуле (19.3) таблицы неопределенных интегралов получаем:

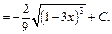
2) Поскольку  то
то 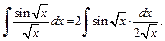 Поднесение под дифференциал приводит далее к интегралу
Поднесение под дифференциал приводит далее к интегралу 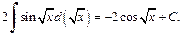
Для вычисления интеграла использовали формулу (19.8) таблицы неопределенных интегралов.
3) Очевидно, что  Значит,
Значит,
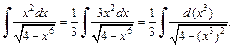
Применяя формулу (19.14) таблицы интегралов, получаем ответ: 
4) Используя второе свойство неопределенного интеграла, представим заданный интеграл в виде суммы двух интегралов:

Вычислим полученные интегралы отдельно. Так как 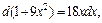 то, используя далее формулу (19.5) таблицы интегралов, получаем:
то, используя далее формулу (19.5) таблицы интегралов, получаем:

Так как 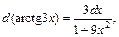 то по формуле (19.3) таблицы интегралов имеем:
то по формуле (19.3) таблицы интегралов имеем:
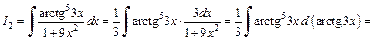

Подставив найденные значения интегралов I 1(x) и I 2(x) в первоначальный интеграл, приходим к ответу: 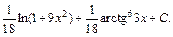
Пример 2. Методом подстановки найти интеграл:
1) 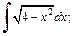 2)
2)  3)
3) 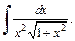
Решение. 1) Используем метод подстановки. Положим  тогда
тогда 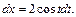



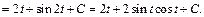
Для вычисления последних интегралов использовали формулы (19.4) и (19.9) таблицы интегралов. Выразим переменную t через переменную x.
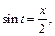
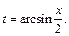 Тогда
Тогда 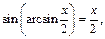
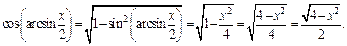
Получаем ответ: 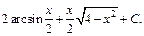
2) Применим подстановку  тогда
тогда 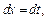
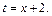 Таким образом,
Таким образом,
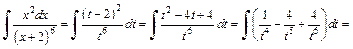
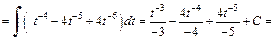

Для вычисления интеграла использовали формулу (19.3) таблицы интегралов.
3) Применим подстановку  тогда
тогда 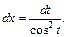 Получаем:
Получаем:

Используя тригонометрическое тождество 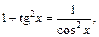 имеем:
имеем:
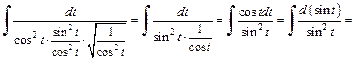

Вернемся к переменной x, для чего выразим t через x из подстановки 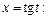
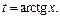 Тогда
Тогда
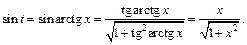 Таким образом,
Таким образом,