
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Свойства неопределенного интеграла
|
|
1. 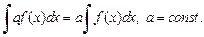
2. 
3. 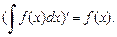
4. 
5. 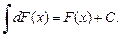
6. Если 
то 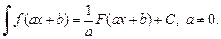
Непосредственным интегрированием называют интегрирование с помощью таблицы неопределенных интегралов, первого и второго свойств неопределенного интеграла и тождественных преобразований подынтегральной функции.
Пример 1. Проверить, является ли функция  первообразной для функции
первообразной для функции 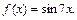
Решение. Найдем производную функции F (x):

Согласно формуле (19.1) функция F (x) является первообразной функции f (x).
Пример 2. Проверить, является ли функция  первообразной для функции
первообразной для функции  найти неопределенный интеграл и нарисовать интегральные кривые из семейства первообразных для
найти неопределенный интеграл и нарисовать интегральные кривые из семейства первообразных для 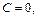
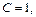
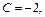
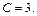
Решение.  По формуле (19.2) неопределенный интеграл имеет вид:
По формуле (19.2) неопределенный интеграл имеет вид:  Построим интегральные кривые (рис. 19.1).
Построим интегральные кривые (рис. 19.1).
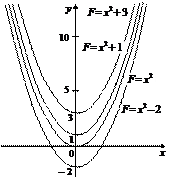
Рис. 19.1
Пример 3. Путем непосредственного интегрирования найти неопределенные интегралы:
1)  2)
2)  3)
3) 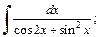
4) 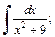 5)
5)  6)
6) 
Решение. 1) Используя первое и второе свойства неопределенного интеграла и формулы (19.3) и (19.5) таблицы интегралов, получаем:


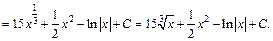
2) Используя второе свойство неопределенного интеграла и формулу (19.6) таблицы интегралов, имеем:
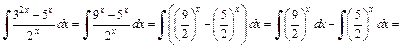

3) Применяя формулу  и формулу (19.10) таблицы интегралов, получаем:
и формулу (19.10) таблицы интегралов, получаем:
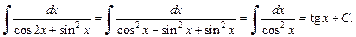
4) С помощью формулы (19.13) таблицы интегралов находим:
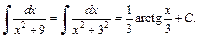
5) Применяя формулу  первое и второе свойства неопределенного интеграла, формулы (19.4) и (19.9) таблицы интегралов, получаем:
первое и второе свойства неопределенного интеграла, формулы (19.4) и (19.9) таблицы интегралов, получаем:
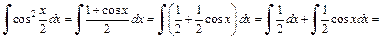

6) С помощью формулы (19.14) таблицы интегралов находим:
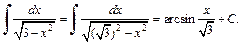
Пример 4. Используя интегрирование дифференциала, найти:
1) 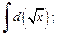 2)
2)  3)
3) 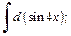 4)
4) 