Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Интегрирование некоторых выражений,
|
|
содержащих квадратный трехчлен 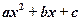
Рассмотрим некоторые виды интегралов, содержащих квадратный трехчлен в подынтегральном выражении, и способы их вычисления. Всюду далее считаем 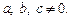
Для вычисления интеграла вида
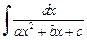 (19.17)
(19.17)
выделим полный квадрат в квадратном трехчлене:
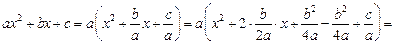
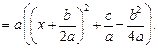
Сделаем замену переменной 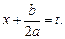 Тогда интеграл (19.17), в зависимости от знака выражения
Тогда интеграл (19.17), в зависимости от знака выражения 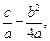 сводится к одному из интегралов
сводится к одному из интегралов  или
или 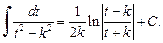
Вместо замены переменной (после выделения полного квадрата) можно использовать также метод поднесения под знак дифференциала.
Интеграл вида
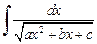 (19.18)
(19.18)
также вычисляется выделением полного квадрата в квадратном трехчлене. Он сводится к интегралу
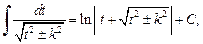 если
если 
или к интегралу
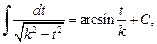 если
если 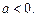
Рассмотрим интеграл вида
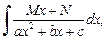 где
где 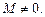 (19.19)
(19.19)
В числителе подынтегральной функции выделяем производную 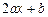 квадратного трехчлена, записанного в знаменателе. Тогда интеграл (19.19) можно представить в виде суммы двух интегралов, один из которых сводится к интегралу
квадратного трехчлена, записанного в знаменателе. Тогда интеграл (19.19) можно представить в виде суммы двух интегралов, один из которых сводится к интегралу 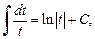 а второй вычисляем как интеграл вида (19.17).
а второй вычисляем как интеграл вида (19.17).
Интеграл вида 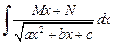 сводится к сумме интегралов
сводится к сумме интегралов 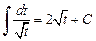 и вида (19.18).
и вида (19.18).
Интегралы вида 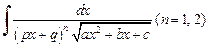 сводятся к рассмотренным выше интегралам с помощью подстановки
сводятся к рассмотренным выше интегралам с помощью подстановки 
Интеграл вида  после выделения полного квадрата и замены
после выделения полного квадрата и замены 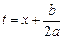 сводится к одному из интегралов
сводится к одному из интегралов 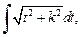
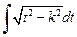 или
или 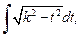 которые могут быть вычислены методом интегрирования по частям (см. п. 19.4.) или с помощью тригонометрических подстановок (см. п. 19.7.), или как интеграл от дифференциального бинома (см. п. 19.8).
которые могут быть вычислены методом интегрирования по частям (см. п. 19.4.) или с помощью тригонометрических подстановок (см. п. 19.7.), или как интеграл от дифференциального бинома (см. п. 19.8).
Пример 1. Найти неопределенный интеграл:
1) 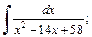 2)
2) 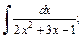
3) 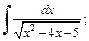 4)
4) 
Решение: 1) Выделим в знаменателе дроби полный квадрат:
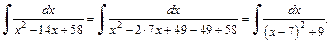
Используем метод поднесения под знак дифференциала. Интеграл примет вид:
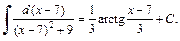
Для вычисления последнего интеграла использовали формулу (19.13) таблицы интегралов.
2) Вынесем в знаменателе подынтегрального выражения множитель 2 за скобки и выделим полный квадрат, получим:
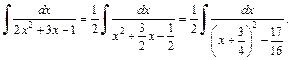
Заменим  и
и 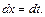 Интеграл примет вид:
Интеграл примет вид:
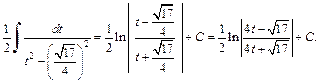
Для вычисления последнего интеграла использовали формулу (19.15) таблицы интегралов. Возвращаясь к переменной x, имеем:
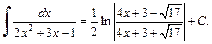
3) Выделив в подкоренном выражении полный квадрат, получаем:
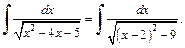
Используя метод поднесения под знак дифференциала и формулу (19.16) таблицы интегралов, имеем:
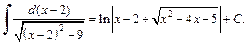
4) Выделим в подкоренном выражении полный квадрат:
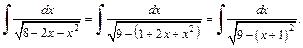
Применив метод поднесения под знак дифференциала и формулу (19.14) таблицы интегралов, получаем:

Пример 2. Найти неопределенный интеграл:
1) 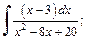 2)
2) 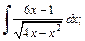 3)
3) 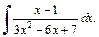
Решение: 1) Найдем производную квадратного трехчлена, записанного в знаменателе дроби, 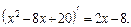
Выделим производную знаменателя в числителе дроби:
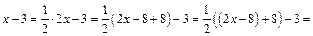
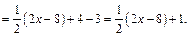
Тогда 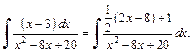
Используя второе свойство неопределенного интеграла, представим данный интеграл в виде суммы двух интегралов

Выделим в знаменателе второго интеграла полный квадрат:
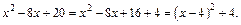
Для вычисления полученных интегралов используем метод поднесения под знак дифференциала и формулы (19.5) и (19.13) таблицы интегралов:

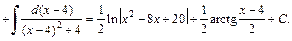
2) Выделим в подкоренном выражении полный квадрат:
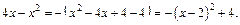
Заменив 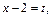
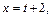
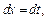 получим:
получим:

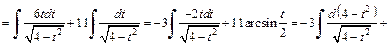
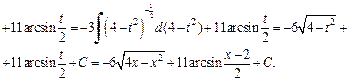
Для вычисления суммы интегралов использовали метод поднесения под знак дифференциала и формулы (19.3) и (19.14) таблицы интегралов.
3) Найдем производную квадратного трехчлена

Выделим ее в числителе дроби, чтобы получить дифференциал знаменателя:
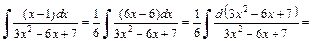
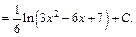
Для вычисления интеграла использовали метод поднесения под знак дифференциала и формулу (19.5) таблицы интегралов.
Пример 3. Найти неопределенный интеграл 
Решение: Применим подстановку 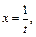 тогда
тогда 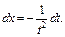 Получаем:
Получаем: