
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Краткая теория. 1. Производной функции называется конечный предел приращения функции к приращению независимой переменной при стремлении последнего к нулю (при условии
|
|
1. Производной функции 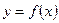 называется конечный предел приращения функции к приращению независимой переменной при стремлении последнего к нулю (при условии, что этот предел существует):
называется конечный предел приращения функции к приращению независимой переменной при стремлении последнего к нулю (при условии, что этот предел существует):
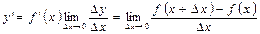 . (7.1)
. (7.1)
Если функция в точке 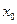 (или на промежутке
(или на промежутке 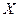 ) имеет конечную производную, то функция называется дифференцируемой в этой точке (или на промежутке
) имеет конечную производную, то функция называется дифференцируемой в этой точке (или на промежутке 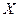 ).
).
2. Если функция 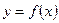 дифференцируема в точке
дифференцируема в точке 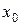 , (или на промежутке
, (или на промежутке 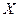 ), то она в этой точке непрерывна (или на промежутке
), то она в этой точке непрерывна (или на промежутке 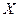 ). Если функция непрерывна в данной точке, то она обязательно дифференцируема в данной точке.
). Если функция непрерывна в данной точке, то она обязательно дифференцируема в данной точке.
1. Используя определение производной, найти производную функции 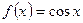 .
.
Решение. Придавая аргументу 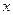 приращение
приращение 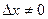 , найдем соответствующее приращение функции:
, найдем соответствующее приращение функции:
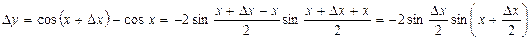 .
.
Составим отношение:
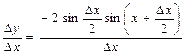 .
.
Найдем предел этого отношения при 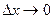 :
:
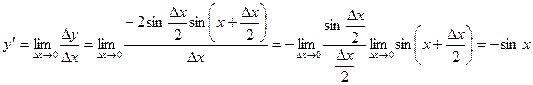
(ибо в силу (6.1) первый предел равен 1).
Таким образом:  .
.
2. Доказать, что функция  непрерывна, но не дифференцируема в точке
непрерывна, но не дифференцируема в точке  .
.
Решение. Функция: 
1) определена на всей числовой оси, в том числе в точке  ;
;
2) существует конечный предел  ;
;
3) этот предел равен значению функции в точке  , т.е.
, т.е. 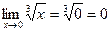 .
.
Таким образом, согласно определению (6.4) непрерывности функции в точке, функция непрерывна при  .
.
Производная функции
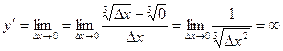 ,
,
т.е. функция не является дифференцируемой при  .
.
Используя определение производной, найти производные функций:
1.  .
.
2. 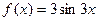 .
.
3. 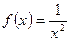 .
.
4. 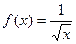 .
.
5.  .
.
6. 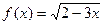 .
.
Доказать, что функции непрерывны и дифференцируемы при 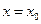 :
:
7.  ,
, 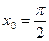 .
.
8. 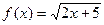 ,
, 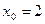 .
.
Доказать, что функции являются непрерывными, но не дифференцируемы при 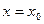 :
:
9. 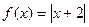 ,
,  .
.
10.  ,
,  .
.
7.2 Правила дифференцирования. Производные элементарных функций.