C учетом второго условия (5.15) можно записать, что

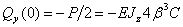, (2.21)

откуда окончательно получим:

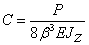. (2.22)

Подставляя (12.22) в (12.19), получим окончательную формулу по определению прогибов балки на упругом основании при действии сосредоточенной силы в следующем виде:

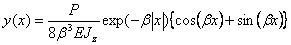. (2.23)

Последовательно определяем выражение изгибающего момента и поперечной силы:

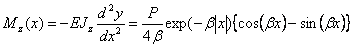. (2.24)

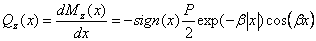. (2.25)

Если в выражениях (2.23)¸ (2.25) принять Р = 1 кН, то эпюры y (0), M_z (0) и Q_y (0) можно трактовать, как линии влияния, соот­ветственно, деформаций, изгибающих моментов и поперечных сил для сечения балки х = 0. Соответствующие эпюры приведены на рис.2.4.

Обратим внимание на тот факт, что согласно (2.25) наибольший изгибающий момент , возникающий под силой P при заданной жесткости балки EJ_z , в большей степени зависит от жесткости основания k, т.к. коэффициент относительной жест­кости основания 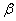зависит от соотношения k и EJ_z . Например, в случае, если балка лежит на жестком основании (k ® ¥ Þ b ® ¥), то M _max ® 0; и, наоборот, в случае, если балка лежит на мягком основании (k ® 0 Þ b ® 0), то M _max®¥. Простым подтверждением этого явления может служить то, что железнодорожные рельсы, уложенные на жесткое основание, могут безболезненно выдер­живать довольно значительные поездные нагрузки. В то же время, те же рельсы, уложенные на слабое основание, либо, если рельс " провисает" (т.е. пространство между шпалами содержит пустоты), могут разрушиться при значительно меньших нагрузках.

2.4. Расчет балки бесконечной длины, нагруженной
системой сосредоточенных сил

Рассмотрим решение следующей задачи. Предположим, что на балку бесконечной длины в точках с абсциссами x_j (j = 1, 2,..., N) приложена система сосредоточенных сил P ₁, P₂, P ₃,..., P_n (рис.2.5).

Рис. 2.5

Рассматривая решение поставленной задачи, на примере рельса верхнего строения пути в качестве балки, лежащей на сплошном упругом основании при действии системы сосредоточенных грузов P ₁, P₂, P ₃,..., P_n, передающихся на путь от подвижного состава.

Железнодорожный путь должен отвечать требованиям прочнос­ти, жесткости и устойчивости при воздействии на него подвижного состава.

Напряжения и деформации, возникающие в опасных сечениях конструкции верхнего строения пути должны удовлетворять усло­виям прочности и жесткости, т.е.

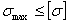; (2.26)

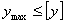, (2.27)

где s_max, y_max - соответственно, максимально возможное значение напряжений и прогибов конструкции в опасных сечениях; 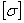, 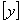- предельно допустимые величины напряжений и прогибов.

В данном случае формулы по определению прогибов, изгиба­ющих моментов и поперечных сил в сечениях с координатами x_n (n = 1, 2,..., N) на основании теоремы о независимости действия внешних сил в упругих системах и теоремы о взаимности можно записать в виде

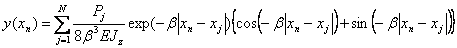. (2.28)

Последовательно определяем выражение изгибающего момента и поперечной силы:

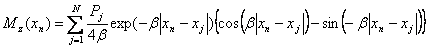. (2.29)

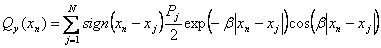. (2.30)

По максимальному значению момента, вычисляемому по (2.29):

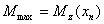, (2.31)

в опасном поперечном сечении рельса в опасных точках вычисля­ется максимальное значение нормальных напряжений:

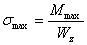, (2.32)

где W_z - момент сопротивления поперечного сечения рельса пути.