
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Расчет коротких балок на упругом основании.
|
|
Функции Крылова

Рис. 2.8
Значительно более сложным оказывается решение для коротких балок, когда требуется учесть условия на обоих концах балки. К таким балкам относится, например, рельсовый путь на шпалах (рис.2.8). Для коротких балок нельзя использовать решения, полученные для балок бесконечной длины и требуется исходить из общего интеграла (2.9), содержащего четыре произвольные постоянные интегрирования. Для решения обычно пользуются нормальными фундаментальными функциями уравнения (2.5). Эти функции называемые функциями Крылова, являются решениями однородного уравнения (2.5) и удовлетворяют специальным условиям при x = 0.
Cоставим следующую таблицу, в которой сведены начальные значения функций Крылова и их производных:
 . (2.34)
. (2.34)
Так как во всех клетках этой таблицы стоят нули, лишь на главной диагонали единицы, то система частных решений Uk, называется системой с единичной матрицей. Эти решения суть:
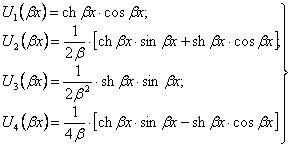 . (2.35)
. (2.35)
Следует отметить, что производные функций Крылова (12.35) выражаются снова через те же функции, причем:
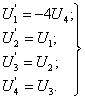 . (2.36)
. (2.36)
Таким образом, общий интеграл уравнения (12.9) может быть представлен через функции Крылова:
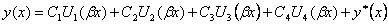 . (2.37)
. (2.37)
Постоянные интегрирования C 1 , C 2 , C 3 , C 4 имеют здесь совершенно определенный смысл. Действительно, если положить x = 0, и воспользоваться свойством (2.34) введенных функций, получим:
 (2.38)
(2.38)
Таким образом:
 . (2.39)
. (2.39)
Формула (2.39) представляет общий интеграл уравнения (2.5). Постоянные интегрирования имеют здесь простой смысл: это начальные (при x = 0) значения искомой функции и ее производные. Поэтому, метод интегрирования дифференциальных уравнений, основанный на формуле (2.39), и широко применяемый в строительной механике, называется методом начальных параметров.
Согласно метода начальных параметров, балка разбивается на участки. Подставив (2.38) в (2.39), получим функцию прогибов на I участке балки:
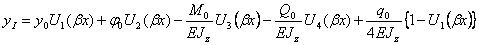 . (2.40)
. (2.40)
Пользуясь приведенными в (12.36) правилами дифференцирования от функций прогибов (12.40) переходим к углам поворота 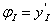 и далее по формулам (12.25), (12.26) к внутренним усилиям на I участке:
и далее по формулам (12.25), (12.26) к внутренним усилиям на I участке:
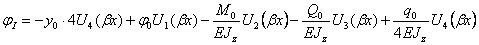 ; (2.41)
; (2.41)
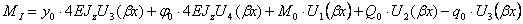 ; (2.42)
; (2.42)
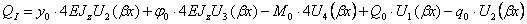 . (2.43)
. (2.43)
Функцию 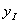 продолжаем на второй и последующие участки. Приращения
продолжаем на второй и последующие участки. Приращения 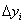 этой функции будут зависеть от приращений внутренних сил
этой функции будут зависеть от приращений внутренних сил 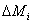 ,
, 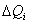 и интенсивности нагрузки на границах между участками
и интенсивности нагрузки на границах между участками 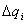 . Добавляя эти приращения к функции прогибов, углов поворота, изгибающих моментов и поперечных сил, получим универсальные формулы:
. Добавляя эти приращения к функции прогибов, углов поворота, изгибающих моментов и поперечных сил, получим универсальные формулы:
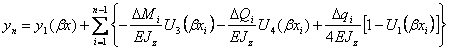 ; (12.44)
; (12.44)
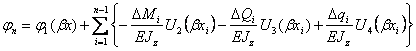 ; (12.45)
; (12.45)
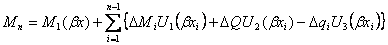 ; (12.46)
; (12.46)
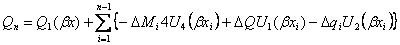 , (12.47)
, (12.47)
здесь для краткости обозначено 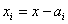 ;
; 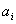 - абсцисса i- ой границы между участками.
- абсцисса i- ой границы между участками.
Как и в обычной балке, в начале координат часть начальных параметров бывает известна, а остальные определяются из граничных условий, формируемых для противоположного конца стержня.
С целью облегчения вычислений при выполнении практических расчетов балок на упругом основании в таблице 12.7 приводятся значения тригонометрических, гиперболических функций и функций Крылова при заданном аргументе.