Теорема 1. Переріз будь-якого числа опуклих на площині множин є опуклою множиною.

Точки (х; у) можна тлумачити не лише як точки площини з координатами х і у, а й як двовимірні вектори 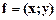з координатами х і у. Тому, якщо дано два вектори 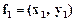і 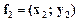, то точки відрізка, що сполучає вектори 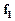і 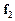, є сукупністю векторів 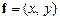, які задовольняють умову

.

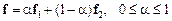У координатній формі останню рівність можна записати у вигляді системи (1).

Означення. Множина Е називається опуклою, якщо для будь-яких двох векторів на площині із Е 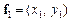, 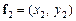і довільного дійсного числа 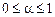вектор 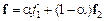належить Е.

Довести, що множина

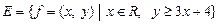
є опуклою.

· Нехай задано вектори 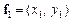і 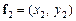із Е та довільне 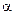, 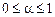. Тоді , , , ,

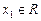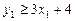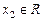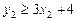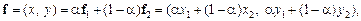
де .

Із 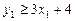, , 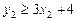, 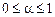випливає:

, ,

,

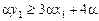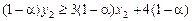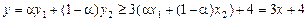тобто 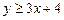, отже, 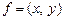належить Е і множина Е є опуклою.●

Показати, що множина

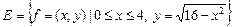
не є опуклою.

Візьмемо із множини Е два вектори 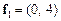і 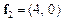. Нехай 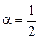, тоді вектор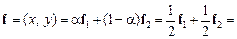 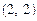не належить Е, оскільки 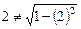. Отже, Е не є опуклою множиною.

Зауваження. Будь-який замкнений, відкритий або напіввід­критий, скінченний або нескінченний проміжок є, очевидно, опуклою множиною.

35. Поняття про опуклі та вгнуті функції

Означення. Функція f (х) називається опуклою на проміжку
[ a, b ], якщо множина

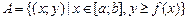
є опуклою.

Із означення бачимо, що А є така множина точок (х; у) площини, абсциси яких належать проміжку [ a, b ], а їх координати не менші від значення функції f (х) у точці х.

На рис. 5.23 зображено графіки функцій, опуклих на відрізку [ a, b ].

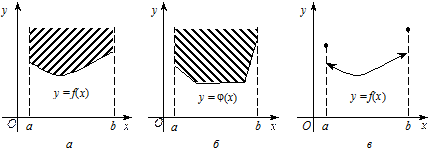
Рис. 5.23

Означення. Функція f (х) називається вгнутою на проміжку
[ a, b ], якщо – f (х) є опуклою на тому самому проміжку.

Геометрична ілюстрація:

Рис. 5.24

На рис. 5.24 зображено графіки вгнутих функцій. Геометрично вгнута функція f (х) на проміжку (а; b) характеризується тим, що множина А розміщена не нижче від графіка у = f (х) на проміжку [ a, b ]. Вгнута функція f (х), навпаки, характеризується тим, що для неї множина А розміщена не вище від графіка у = f (х) на проміжку [ a, b ].

36. Ознаки опуклості та вгнутості функцій.
Строго опуклі і строго вгнуті функції