
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Для того щоб функція f(х) була вгнутою на проміжку [а; b], необхідно і достатньо, аби виконувалася умова: для довільних х1 і х2 із [а; b] і будь-якого a, 0 £ a £ 1
|
|
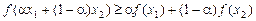 . (3)
. (3)
Означення. 1. Функція f (х) на проміжку [ a; b ] називається опуклою (вгнутою), якщо для будь-яких двох точок х 1 і х 2 із [ a; b ] і будь-якого a, 0 £ a £ 1, виконується нерівність
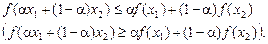
2. Функція f (x) на проміжку [ a, b ] називається строго опуклою (строго вгнутою), якщо для будь-яких точок х 1 і х 2 із [ a, b ], х 1 ¹ х 2, і будь-якого a, 0 < a < 1, виконується нерівність
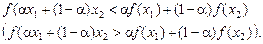
Геометрична ілюстрація
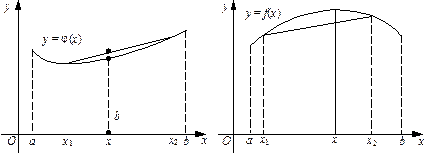
Рис. 5.25 Рис. 5.26
Геометрично умова (2) означає, що точки хорди, яка сполучає дві точки графіка опуклої функції f (x), лежать не нижче від графіка функції. Для строго опуклої функції точки такої хорди лежать вище від графіка функції, тобто якщо f (x) — строго опукла функція, то для будь-яких двох точок (х 1; f (x 1)) і (х 2; f (x 2)), х 1 < x < x 2, хорда, що сполучає ці дві точки, має задовольняти умову у > f (x).
У разі строго вгнутої функції f (x), навпаки, для точок (х; у) хорди, яка сполучає точки (х 1; f (x 1)), (х 2; f (x 2)) графіка у = f (x) має виконуватись умова у < f (x).
На рис. 5.25 і 5.26 подано графіки строго опуклої і строго вгнутої функцій.
 Лінійна функція f (x) = аx + b опукла і одночасно вгнута (не строго), оскільки для неї одночасно виконуються умови (1) і (2), в яких нестрогі нерівності перетворюються на рівності.
Лінійна функція f (x) = аx + b опукла і одночасно вгнута (не строго), оскільки для неї одночасно виконуються умови (1) і (2), в яких нестрогі нерівності перетворюються на рівності.
 Показати, що функція f (x) = x 2 строго опукла для дійсних х.
Показати, що функція f (x) = x 2 строго опукла для дійсних х.
● Справді, нехай х 1 і х 2 — дійсні числа, х 1 ¹ х 2. Тоді
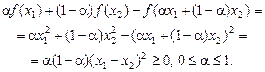
Отже, за умовою (1) функція f (x) = x 2 опукла; для x 1 = x 2 і
0 < a < 1 дістанемо строгу нерівність, звідки f (x) = x 2 — строго опукла функція.
Без доведення наведено такі ознаки опуклості.