
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теорема. Крива , тоді і тільки тоді має асимптоту , коли існують скінченні границі
|
|
Похилі асимптоти.
Означення. Нехай функція 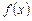 визначена в інтервалі
визначена в інтервалі 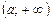 або в інтервалі
або в інтервалі 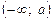 . Пряму
. Пряму 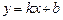 називатимемо асимптотою кривої
називатимемо асимптотою кривої 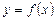 , якщо виконується умова
, якщо виконується умова
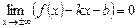 .
.
Геометрична ілюстрація (рис. 5.48). Різниця ординат кривої 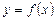 і прямої
і прямої 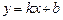 прямує до нуля, коли їх абсциси прямують до нескінченності:
прямує до нуля, коли їх абсциси прямують до нескінченності: 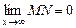 .
.

Рис. 5.48
Теорема. Крива, тоді і тільки тоді має асимптоту, коли існують скінченні границі
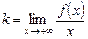 ,
, 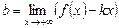 . (1)
. (1)
 Знайти асимптоти функції
Знайти асимптоти функції 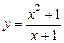 .
.
· У точці 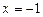 функція має розрив другого роду, тому
функція має розрив другого роду, тому 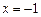 — вертикальна асимптота. Знайдемо похилу асимптоту. За теоремою
— вертикальна асимптота. Знайдемо похилу асимптоту. За теоремою
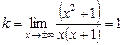 ,
, 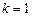 .
.
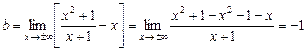 ,
, 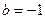 .
.
Отже, пряма 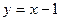 є асимптотою функції при
є асимптотою функції при 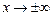 (рис. 5.49).
(рис. 5.49).
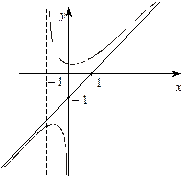
Рис. 5.49
 Чи має функція
Чи має функція 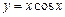 похилі асимптоти?
похилі асимптоти?
· Функція 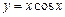 похилих асимптот не має, оскільки не існує границі
похилих асимптот не має, оскільки не існує границі 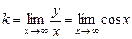 .
.
 Знайти похилі асимптоти кривої
Знайти похилі асимптоти кривої 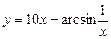 .
.
· Областю визначення кривої є частина площини, де 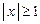 . Застосовуючи теорему про побудову асимптот, дістаємо
. Застосовуючи теорему про побудову асимптот, дістаємо
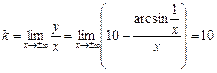 ,
,
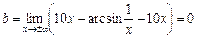 .
.
Отже, пряма 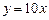 є асимптотою кривої при
є асимптотою кривої при 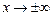 .
.
3. Горизонтальні асимптоти. Якщо в похилій асимптоті 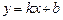 функції
функції 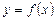 маємо
маємо 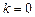 , то таку похилу асимптоту називають горизонтальною асимптотою функції. Отже, горизонтальна асимптота — частинний випадок похилої — відшукується як похила асимптота за умов
, то таку похилу асимптоту називають горизонтальною асимптотою функції. Отже, горизонтальна асимптота — частинний випадок похилої — відшукується як похила асимптота за умов
 ,
, 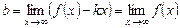
і має вигляд 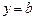 . До речі, умову
. До речі, умову 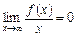 можна не перевіряти, якщо
можна не перевіряти, якщо 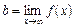 — скінченна границя, оскільки в такому разі границя
— скінченна границя, оскільки в такому разі границя 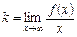 завжди дорівнює нулю. Звідси можемо зробити висновок.
завжди дорівнює нулю. Звідси можемо зробити висновок.
Для того щоб пряма 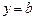 була горизонтальною асимптотою функції
була горизонтальною асимптотою функції 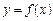 ,
, 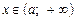 ,
, 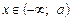 , необхідно і достатньо, щоб існувала скінченна границя
, необхідно і достатньо, щоб існувала скінченна границя 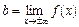 .
.
 Знайти горизонтальні асимптоти функції
Знайти горизонтальні асимптоти функції  .
.
· Маємо
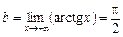 ,
, 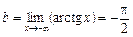 .
.
Отже,  горизонтальні асимптоти (5.50).
горизонтальні асимптоти (5.50).

Рис. 5.50
5.7.3. Загальний план дослідження функції
1. Знайти область визначення та значення функції, заданої формулою, якщо таку область не зазначено.
2. Дослідити функцію на парність, непарність, періодичність.
3. З’ясувати точки перетину функції з вісями координат.
4. Дослідити функцію на неперервність.
5. Знайти асимптоти графіка функції (якщо вони існують).
6. З’ясувати, як функція поводиться на кінцях кожного з проміжків області визначення (знайти границі функції на кінцях цих проміжків, якщо вони є).
7. Дослідити функцію на диференційовність.
8. Дослідити функцію на монотонність та екстремуми. Знайти екстремуми і значення функції в точках екстремуму.
9. Дослідити функцію на опуклість (вгнутість): знайти інтервали опуклості (вгнутості), а також точки перегину функції.
10. Знайти найбільше і найменше значення функції (якщо вони існують).
11. Побудувати графік функції.
 Побудуємо графік функції
Побудуємо графік функції  .
.
1. Функція не існує в точках 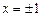 . Тому область визначення функції
. Тому область визначення функції
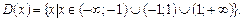
2. Функція непарна, оскільки 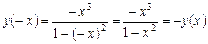 . З огляду на непарність функції достатньо побудувати її графік лише при
. З огляду на непарність функції достатньо побудувати її графік лише при 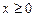 .
.
Функція неперіодична.
3. Точки перетину з осями координат:
з віссю Ох: 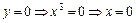
(0; 0) — точка перетину з віссю Ох.
з віссю Оу: 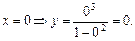
(0; 0) — точка перетину з віссю Оу.
4. Функція невизначена в точці  тому ці точки є «підозрілими» на розрив. Знайдемо односторонні границі в точці
тому ці точки є «підозрілими» на розрив. Знайдемо односторонні границі в точці 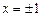 :
:
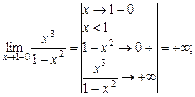

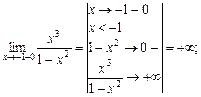
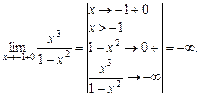
Точки 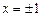 — точки розриву другого роду.
— точки розриву другого роду.
 — область неперервності функції.
— область неперервності функції.
5. Знаходимо асимптоти функції. Насамперед з’ясовуємо, що прямі 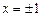 — вертикальні асимптоти. (Це випливає з означення вертикальних асимптот та п. 4.)
— вертикальні асимптоти. (Це випливає з означення вертикальних асимптот та п. 4.)
Шукаємо похилу асимптоту 
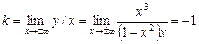 ;
;
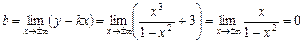 .
.
Отже,  — похила асимптота.
— похила асимптота.
6. В п. 4 знайдені односторонні границі функції в точках 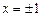 . Залишилось знайти границі функції, коли
. Залишилось знайти границі функції, коли 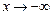 і
і 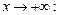
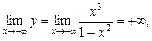
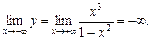
7. Знайдемо першу похідну від функції у (вона існує на D (x)):

8. Дослідимо функцію на монотонність і знайдемо точки екстремуму. Для знаходження стаціонарних точок прирівнюємо першу похідну до нуля:
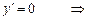
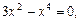
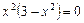

Зважаючи на зауваження п. 2, розглядатимемо дослідження функції при 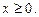
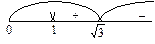
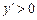 , коли
, коли 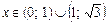 ,
,
 , коли
, коли 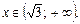
Тому 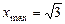 — точка максимуму,
— точка максимуму, 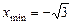 — точка мінімуму.
— точка мінімуму.
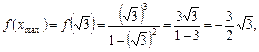
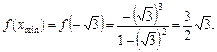
9. Знайдемо другу похідну функції у:
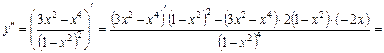
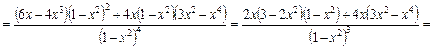

Точка х = 0 може бути точкою перегину, бо 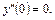 Перевіримо це за критерієм. Визначимо знак
Перевіримо це за критерієм. Визначимо знак 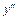 в околі точки х = 0
в околі точки х = 0
Друга похідна змінює в точці х = 0 свій знак, тому функція 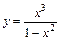 має точку перегину х = 0, на проміжку (0; 1) функція опукла, (1, +∞) — функція вгнута.
має точку перегину х = 0, на проміжку (0; 1) функція опукла, (1, +∞) — функція вгнута.
10. Найбільше та найменше значення функції не існують.
11. Побудуємо графік функції, враховуючи дослідження.
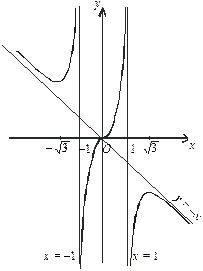
Рис. 5.51