Геометрична ілюстрація

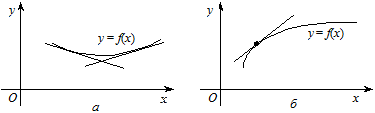
Рис. 5.27

Зауваження. У деяких підручниках розглядаються тільки строго опуклі і строго вгнуті диференційовні функції. Дослідження на опуклість і вгнутість зводиться до дослідження монотонності її похідної f¢ (x). Якщо функція f (x) двічі диференційовна, то для дослідження f¢ (x) на монотонність можна застосувати критерій для нестрогої і строгої монотонності функції на проміжку. При цьому графік строго опуклої функції f (x) називають кривою у = f (x), повернутою опуклістю вниз (або кривою, повернутою вгнутістю вгору), а графік строго вгнутої функції f (x) називають кривою у = f (x), повернутою вгнутістю (або кривою, повернутою опуклістю вгору).

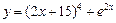Показати, що крива всюди вгнута догори.

● Маємо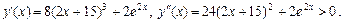

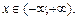
За наслідком із теореми функція 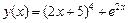строго опукла в інтервалі (– ¥; + ¥), отже, крива скрізь вгнута догори.

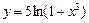Дослідити криву на напрямок вгнутості.

● Функція 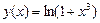визначена в інтервалі (– 1; + ¥). У цьому інтервалі

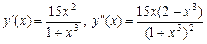
і 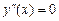в точках х ₁ = 0 і .

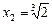Методом інтервалів знаходимо, що 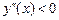в інтервалі (–1; 0), 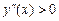в інтервалі і 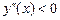в інтервалі . За наслідком із теореми доходимо висновку, що в інтервалах (– 1; 0) і крива вгнута донизу, а в інтервалі 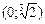вгнута вгору.

38. Точки перегину

Нехай функція f (x) диференційовна в інтервалі (а; b) за винятком, можливо, точки с Î (а; b), в якій вона неперервна і або не диференційовна, або має нескінченну похідну.

Означення. Точка с називається точкою перегину кривої
у = f (x), де х Î (а; b), якщо існує такий окіл точки с, в якому для
х < с крива у = f (x) опукла, а для х > с крива у = f (x) вгнута, або якщо для х < с крива у = f (x) вгнута, а для всіх х > с опукла.

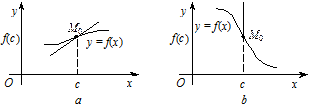
Рис. 5.28

При цьому точку графіка (с; f (c)) також називають точкою перегину (рис. 5.28).

Геометрична інтерпретація. Точка с є точкою перегину кривої, якщо при переході через точку с крива у = f (x) має перегин, переходячи від опуклої до вгнутої, або навпаки. У самій же точці с функція f (x) або диференційовна, тобто крива у = f (x) має дотичну, не паралельну осі Оу, або неперервна (має дотичну, паралельну осі Оу).

Знайти точки перегину кривої .

· Маємо

.

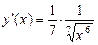Для х < 0 похідна у ¢ (х) є зростаючою, а для х > 0 — спадною. Звідси для х < 0 крива вгнута вгору, а для х > 0 вгнута вниз, в точці
х = 0 функція неперервна і має нескінченну похідну. Отже, точка х = 0 є точкою перегину. Інших точок перегину немає (рис. 5.29).

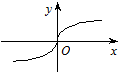
Рис. 5.29

39. Необхідна і достатня умови
існування точок перегину

Теорема 1 (необхідна умова). Нехай функція f (x) двічі диференційовна в околі точки с і функція f² (х) неперервна в точці с. Якщо точка с є точкою перегину кривої у = f (x) тоді f² (с) = 0.

Із означення точки перегину кривої у = f (x) та умов опуклих диференційовних функцій випливають такі достатні умови наявності точок перегину.

Теорема 2. Якщо функція f (x) диференційовна в деякому околі точки с і для х < с цього околу f¢ (х) зростає, а для х > с спадає або, навпаки, для х < с похідна f¢ (х) спадає, а для х > с зростає, то х = с буде точкою перегину у = f (x).

Теорема 3. Якщо функціяf(x)двічі диференційовна в деякому околі точки с іf² (х) < 0длях < сцього околу, а f² (х) > 0длях > сабо, навпаки, f² (х) > 0для х < с, а f² (х) < 0длях > с, то точка сбуде точкою перегину кривої.

Знайдемо точки перегину кривої .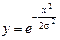

· Знайдемо першу та другу похідну функції:

; ,

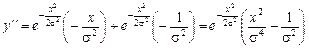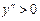, якщо ;

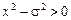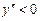, якщо ;

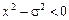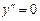, якщо .

Отже, точки є точками перегину

·

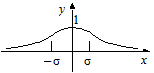Рис. 5.30.

40. Ознака сталості
диференційовних функцій. Зростання і спадання функції

Теорема 1. Нехай функціяf(x)неперервна на проміжку [a; b]і диференційовна в кожній його внутрішній точці. Для того щоб функціяf(x)була сталою на проміжку[a; b], необхідно і достатньо, аби для всіх.

Означення. Нехай функція f (x) визначена на проміжку (a; b) і х ₀Î (a; b). Кажуть, що f (x) зростає в точці x ₀, якщо існує окіл точки x ₀, в якому f (x) < f (x ₀) для х < x ₀, а для х > x ₀

f (x) > f (x ₀).

Аналогічно за означенням f (x) спадає в точці х ₀Î (a; b), якщо існує її окіл, в якому f (x) > f (x ₀) для х < x ₀, а f (x) < f (x ₀) для х > x ₀.

Теорема 2 (достатня ознака зростання і спадання функції в точці). Якщо функція f(x) диференційовна в точці х0Î (a; b) і f¢ (x0) > 0 (f¢ (x0) < 0), то f(x) зростає (спадає) в точці х0.