Принуждённые и свободные токи в цепях.

Любой переменный ток представляет собой колебательный процесс, который связан с обменом энергией между реактивными элементами цепей – индуктивными и ёмкостными сопротивлениями. Из теории колебаний известно, что их можно разделить на свободные и вынужденные. С математической точки зрения наличие правой части в дифференциальном уравнении колебательного процесса (неоднородном) означает, что решение его состоит из двух слагаемых: общего решения однородного уравнения (без правой части) и частного решения неоднородного уравнения.

В качестве последнего выступает режим установившихся колебаний, который определяется методами, изложенными в предыдущих разделах. В электротехнической литературе этот режим именуется принуждённым током, а в радиотехнической – вынужденными колебаниями.

В противовес им свободный ток или свободные колебания возникают при изменении условий поступления в цепи энергии извне, что связано с коммутационными процессами.

Изменение состояния цепи от одного установившегося процесса к другому при коммутации источников энергии или элементов цепи называется переходным процессом. Расчёт переходного процесса сводится к следующим стадиям.

1. Составление дифференциального уравнения. Используется второй закон Кирхгофа, если цепь неразветвлённая, либо выделяются замкнутые независимые контуры с токами, и для каждого составляется своё уравнение, и все уравнения решаются совместно.

2. Решение уравнения производится двумя путями: классическим, с использованием корней характеристического уравнения, либо операторным методом, переводящим расчёт в плоскость алгебры с последующим использованием таблиц изображений.

3. Расчёт принуждённого процесса любым способом.

4. Нахождение постоянных интегрирования, для чего используются две теоремы:

- напряжение на конденсаторе до коммутации равно напряжению после коммутации(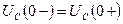

- ток через индуктивность после коммутации равен току до коммутации .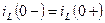

5. Суммирование принуждённого и свободного токов с учётом постоянных интегрирования.

Пример 9.

Расчёт переходного процесса при включении нагрузки с емкостной нагрузкой под переменное напряжение.

, , , .

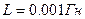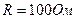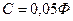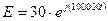1. Составление дифференциального уравнения.

Используя модели (6), (7), (8) и второй закон Кирхгофа (22), нетрудно получить уравнение

,

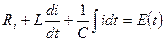дифференцирование по 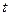даёт каноническую форму уравнения:

.

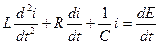Характеристическое уравнение получается заменой второй производной на 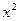, первой – на 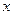, искомого тока 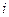– на .

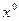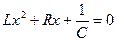, или .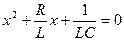

Данное уравнение имеет два корня, которые при подстановке исходных данных имеют величину

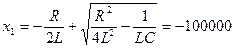
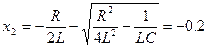
При двух действительных корнях решение однородного дифференциального уравнения имеет вид .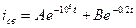

Постоянные интегрирования могут быть найдены из двух начальных условий:

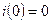(ток до замыкания цепи отсутствует),

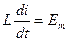(в момент замыкания возникает ЭДС самоиндукции, препятствующая скачку тока через индуктивность).

Следовательно, , .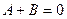

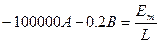Откуда 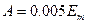, 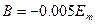. Окончательно в данном случае свободный ток определяется выражением: .

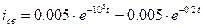Принуждённый ток легко определяется по закону Ома .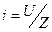

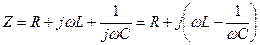
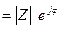
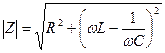
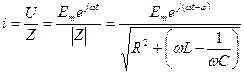
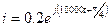A.

Таким образом, полный ток определится выражением

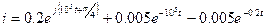
Задание: постройте график i(t) с помощью программы DERIVE.